Лабораторная работа 6 Модели класса ARIMA Пакет Statistica 6.0 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ
реклама
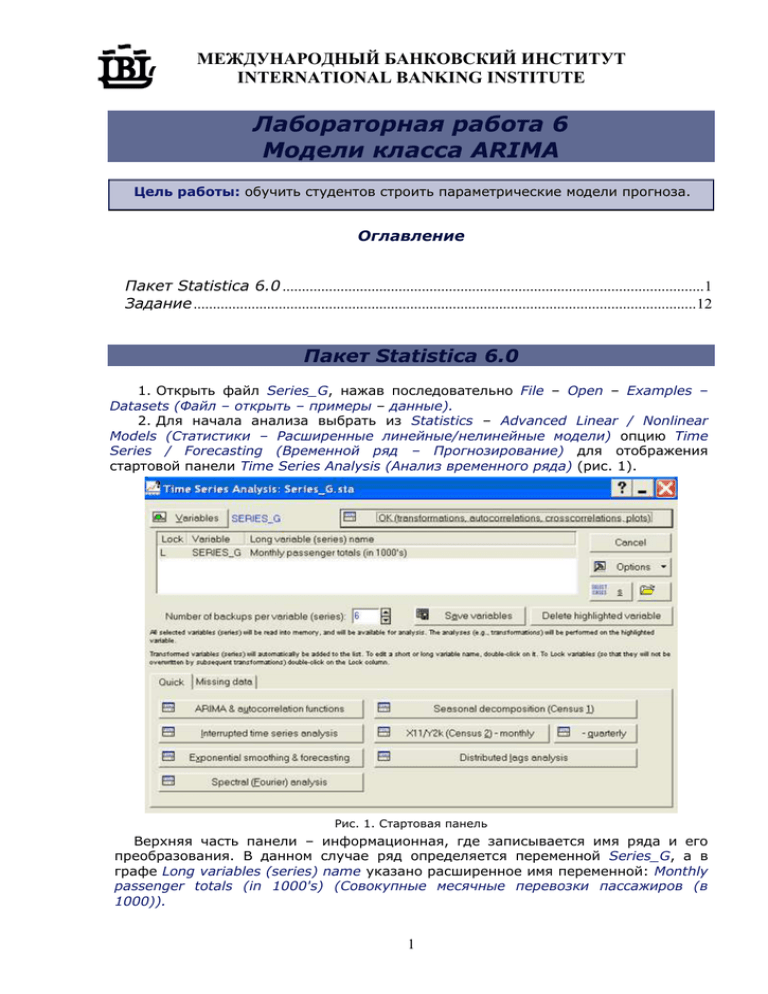
МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Лабораторная работа 6 Модели класса ARIMA Цель работы: обучить студентов строить параметрические модели прогноза. Оглавление Пакет Statistica 6.0 .............................................................................................................1 Задание ..................................................................................................................................12 Пакет Statistica 6.0 1. Открыть файл Series_G, нажав последовательно File – Open – Examples – Datasets (Файл – открыть – примеры – данные). 2. Для начала анализа выбрать из Statistics – Advanced Linear / Nonlinear Models (Статистики – Расширенные линейные/нелинейные модели) опцию Time Series / Forecasting (Временной ряд – Прогнозирование) для отображения стартовой панели Time Series Analysis (Анализ временного ряда) (рис. 1). Рис. 1. Стартовая панель Верхняя часть панели – информационная, где записывается имя ряда и его преобразования. В данном случае ряд определяется переменной Series_G, а в графе Long variables (series) name указано расширенное имя переменной: Monthly passenger totals (in 1000's) (Совокупные месячные перевозки пассажиров (в 1000)). 1 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Нажав кнопку Variables (Переменные), выбрать переменную (здесь она единственная) и щелкнуть ОК. Затем необходимо нажать клавишу ARIMA & autocorrelation functions (ARIMA и автокорреляционные функции) для входа в диалог Single Series ARIMA (Одиночный ряд ARIMA) (рис. 2). Рис. 2. Панель диалога ARIMA 3. Идентификация. Перед тем, как определять оцениваемые параметры в модели ARIMA, последняя должна быть вначале идентифицирована. Хотя большинство необходимых опций (например, Autocorrelations or Partial autocorrelations – Автокорреляции или частные автокорреляции) доступны из этого диалогового окна, здесь будут использованы некоторые опции преобразования для иллюстрации сущности процесса ARIMA. Вследствие этого нужно нажать кнопку Other transformations & plots (Другие преобразования и графики), которая появляется при выделенной опции Advanced (Расширенная). В результате этих действий появляется диалоговое окно Transformations of Variables (Преобразования переменных) (рис. 3). В этом окне вначале надо выбрать более подходящий масштаб для горизонтальной оси. При выделенной опции Review & plot (Просмотр и графики) поставить метку в окне Scale X axis in plots manually (Масштаб Х на графиках вручную) и ввести 1 в качестве Min, а число 12 как Step (Шаг). Кроме того, данный файл содержит названия строк с соответствующими датами для каждого наблюдения, поэтому в окне Label data points with (Метка данных точек с …) необходимо отметить позицию Case names (Названия строк) (рис. 4). 2 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Рис. 3. Диалоговое окно преобразования переменных Для графического отображения ряда нужно щелкнуть кнопку Plot (График), соответствующей выделенной клавише Review highlighted variable (Просмотр высвеченной переменной). На графике четко проявляются тренд и сезонность, поэтому для определения разностей в модели ARIMA позже воспользуемся автокорреляционной и частной автокорреляционной функциями. Рис. 4. Диалоговое окно при выделенной опции Review & plot 3 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE 4. Мультипликативная сезонность. Из графика ряда (рис. 5) видно, что амплитуда сезонных изменений увеличивается со временем, что может привести к смещенным оценкам автокорреляции. Вследствие этого проведем преобразование данных, взяв от них натуральный логарифм, что должно стабилизировать вариации ряда. Рис. 5. Исходный ряд В диалоговом окне преобразования переменных выделить опцию x=f(x) и отметить такое преобразование: Natural log (x=ln(x)). Далее нажать кнопку ОК (Transform selected series) (Преобразования выделенного ряда). После того, как все наблюдения будут преобразованы, появится трансформированный временной ряд (рис. 6). Отметим, что желаемый эффект достигнут, т. к. амплитуда изменений почти стабилизировалась, и ряд готов для дальнейшего анализа автокорреляций. 5. Автокорреляции. Выделить опцию Autocorrs (Автокорреляции) и изменить в окне Autocorrelations & crosscorrelations (Автокорреляции и кросскорреляции) параметр Number of lags (Число лагов) с 15 на 25. Затем нажать клавишу Autocorrelations (Автокорреляции) для отображения таблицы и графика автокорреляционной функции (рис. 7). График показывает сильную последовательную зависимость для лагов от 1 до 12 с максимальной величиной автокорреляции при лаге, равном 1. 4 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Рис. 6. Трансформированный временной ряд Рис. 7. График автокорреляционной функции 5 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE 6. Дифференцирование. Для устранения последовательной зависимости вначале необходимо выполнить дифференцирование ряда с лагом 1. (Отметим, что преобразованный (логарифмированный) ряд автоматически высветился в активной рабочей области.) Выделив опцию Difference, integrate (Дифференцирование, интегрирование), следует указать преобразование Differencing (x=x-x(lag)) и нажать ОК (Transform selected series) (Преобразование выделенного ряда). После выполнения преобразований на экране вновь появится преобразованный временной ряд (рис. 8). Рис. 8. Преобразованный временной ряд Теперь каждый элемент преобразованного ряда представляет разность между своим предыдущим и последующим значениями. При этом ряд стал короче на число элементов, равное лагу, т. е. 1, т. к. первый элемент ряда не участвует в этой операции. Далее необходимо вернуться к диалогу Transformations of Variables (Преобразования переменных), выделить опцию Autocorrs (Автокорреляции) и нажать кнопку Autocorrelations (Автокорреляции). Как видно из графика (рис. 9), теперь не только зависимости первого порядка исчезли, но и большинство других зависимостей также стало достаточно малым. 7. Сезонная последовательная зависимость. Как видно из графика, устранение зависимостей низкого порядка показало, что проявляются зависимости высокого порядка (с лагом 12). Здесь наблюдается явная сезонная зависимость с лагами, равными 24, 36 и т. д., что отражает сезонность авиаперевозок. Дифференцирование с лагом 12 позволит устранить сезонность. Для этого необходимо вернуться к опции Difference, integrate (Дифференцирование, интегрирование), выбрать преобразование 6 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Рис. 9. График автокорреляционной функции после преобразований Differencing (x=x-x(lag)), но с измененным лагом, равным 12, и нажать ОК (Transform selected series) (Преобразование выделенного ряда). Как и прежде, появится график нового временного ряда. Теперь нажать кнопку Partial autocorrelations (Частные автокорреляции) и просмотреть график. 8. Оцениваемые параметры. Коррелограмма не показывает значимых выбросов, поэтому ряд готов для подбора модели. Основываясь на природе ряда, выбираем модель ARIMA с сезонностью, определяемой лагом = 12, и несезонностью с лагом = 1. Таким образом, здесь нужно оценить 2 параметра модели скользящего среднего: сезонный (Q) и несезонный (q). Никаких параметров авторегрессии в данном случае не оценивается. Модифицированный ряд теперь может быть подставлен непосредственно в модель ARIMA. Однако в случаях, подобных рассматриваемому, рекомендуется проанализировать исходный ряд и выбрать необходимые модификации данных как часть спецификаций модели. Вследствие этого ARIMA будет «знать» о модификациях, поэтому при необходимости прогнозирования оценки прогноза будут вычисляться из проинтегрированных (обратных дифференцированию) и ремодифицированных (обратных преобразованию) данных. Такие прогнозные оценки оказываются простыми для интерпретации. 9. Диалог ARIMA. Теперь надо вернуться к диалогу Single Series ARIMA (Единственный ряд ARIMA), нажав кнопку Cancel (Отменить) в окне Transformations of Variables (Преобразования переменных). В окне Single Series ARIMA (Единственный ряд ARIMA) выделить исходную переменную Series_G. Этот диалог позволит определить параметры авторегрессии и скользящего среднего (сезонное и несезонное). Нельзя перейти к следующему шагу до тех пор, пока один из параметров не будет выбран (p, P, q или Q). Однако вначале нужно 7 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE определить преобразования и дифференцирования (разности). При выделенной опции Quick (Быстрая) в окне Transform variable (series) prior to analysis (Преобразование переменной (ряда) для анализа) отметить позиции Natural Log (Натуральный логарифм) и Difference (Разность). Теперь укажем в окнах 1. Lag = 1 и N. Of passes = 1, что определяет логарифмическое преобразование и несезонную простую разность. Для определения сезонности укажем в окнах 2. Lag лаг= 12 и N. of passes = 1 (рис. 10). Рис. 10. Диалоговое окно ARIMA 10. Параметры ARIMA. На стадии идентификации было решено оценить 2 параметра скользящего среднего: один регулярный q и один сезонный Q. В окне параметров надо установить значения q=1 и Q=1, после чего нажать ОК. После процесса оценивания параметров в окне Single Series ARIMA Results (Результаты) появятся результаты расчета (рис. 11). 8 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Рис. 11. Окно результатов расчета Итог приведен в верхней части окна (модель, преобразования). После нажатия кнопки Summary: Parameter estimates (Итоги: оценки параметров) появится таблица результатов (табл. 1), откуда видно, что параметры скользящего среднего (сезонный и несезонный) являются высоко значимыми. Таблица 1. Результаты расчетов 11. Фаза прогнозирования. При выделенной опции Advanced (Расширенная) появляется окно Forecasting (Прогнозирование). По умолчанию этот пакет будет вычислять прогнозы, начиная с последнего наблюдения на один полный сезонный цикл (на 12 месяцев, начиная с момента времени, равного 145). Вначале рассмотрим прогнозы в таблице, нажав кнопку Forecast cases (Прогнозы). Затем можно проанализировать график прогноза, нажав кнопку Plot series & forecasts (График ряда и прогноза) (рис. 12). Здесь можно также рассмотреть, как ведет себя модель прогноза на реальных данных, поставив в окне начала прогноза цифру 133 (145-12+1=133). 9 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Рис. 12. График прогноза 12. Анализ остатков. Для модели ARIMA устанавливаются два допущения об остатках: остатки должны быть нормально распределены; остатки должны быть независимы друг от друга (отсутствует остаточная последовательная корреляция). Первое допущение может быть проверено рассмотрением графика нормального распределения остатков. При выделенной опции Distribution of residuals (Распределение остатков) нажать клавишу Normal probability plots (Нормальные графики). Если остатки нормально распределены, то все точки должны группироваться около прямой линии на графике (рис. 13). 10 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Рис. 13. График нормального распределения остатков Второе допущение проверяется с помощью вычисления автокорреляционной функции: при выделенной опции Autocorrelations (Автокорреляции) нажать кнопку Autocorrelations (Автокорреляции) (рис. 14). Рис. 14. График автокорреляций остатков 11 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Из графика видно, что автокорреляция остатков практически отсутствует, следовательно, условие независимости остатков выполнено для выбранной модели. Задание Построить смоделированный временной ряд в пакете Statistica следующим образом: 1. Создать новый файл, состоящий из 100 строк и 1 столбца. 2. Через меню Data – Variable Specs (Данные – описание переменной) ввести в окно формул выражение =vnormal(rnd(1);1;3). 3. Смоделировать 100 значений случайной нормально распределенной величины с математическим ожиданием, равным 1, и среднеквадратичным отклонением, равным 3. Эти 100 значений определяют переменную Var 1. Перевести их к целому типу данных, установив в окне описания переменной в качестве Type значение Integer. 4. Провести прогнозирование полученного ряда с помощью подбора модели класса ARIMA. 12