проблемы, ошибки, пути их преодоления

Нижегородский государственный университет
им. Н.И.Лобачевского
Факультет Вычислительной математики и кибернетики
Параллельные численные методы
Компьютерная арифметика
При поддержке компании Intel
Бастраков С.И., Донченко Р.В.
Кафедра математического обеспечения ЭВМ
Содержание
Введение
 Представление и свойства чисел с плавающей запятой
 Особенности реализаций
 Литература

Авторы выражают благодарность Florent de Dinechin
(университет Лиона, Франция), за полезные обсуждения и
предоставленные материалы
Н.Новгород, 2012 г.
Параллельные численные методы.
2 из 83
Введение…



Результат выполнения программы зависит не только от её
текста и входных данных, но и от интерпретации текста
компьютером.
Для вычислительных программ особый интерес
представляет интерпретация конструкций языка, связанных
с числами: численных типов данных и численных
выражений.
Комбинацию всех сущностей, отвечающих за эту
интерпретацию — в их число обычно входят транслятор
языка, операционная система и сам компьютер —будем
называть вычислительной системой.
Н.Новгород, 2012 г.
Параллельные численные методы.
3 из 83
Введение

Незнание того, как в вычислительной системе
организована работа с числами, может привести к
существенным (и часто необъяснимым без проведения
тщательного анализа) отклонениям результатов от
ожидаемых.
– Особенно при использовании чисел с плавающей
запятой.
Н.Новгород, 2012 г.
Параллельные численные методы.
4 из 83
Пример ошибки – “Patriot bug”…




“Patriot Missile Software Problem” или “Patriot bug” – одна из
наиболее известных ошибок, вызванных неаккуратным
использованием компьютерной арифметики вещественных
чисел.
Ошибка в работе систем ПВО 25 февраля 1991 года.
Конкретно, в модуле, отслеживающем цель на радаре и
вычисляющем место для следующего сканирования.
Использовались 24-битные числа с фиксированной запятой,
шаг по времени был равен 0,1 секунды.
Число 0,1 не является точно представимым в
использованном формате, из-за этого время в программе
отличалось от реального времени и эта ошибка
накапливалась по мере работы системы.
Н.Новгород, 2012 г.
Параллельные численные методы.
5 из 83
Пример ошибки – “Patriot bug”



После 100 часов последовательной работы разница
составила 0,34 секунды, что при скорости цели в 1,7 км/с
привело к расхождению расчетного места сканирования и
реального положения цели примерно в 0,5 километра.
В результате цель не была захвачена и была отмечена
системой как ложная, ракета-перехватчик не была
выпущена, что привело к гибели 28 человек.
Данная ошибка не могла произойти, если бы шаг по
времени являлся точно представимым в виде 24-битного
числа с фиксированной точкой либо, при сохранении шага,
система регулярно перезагружалась (что было
рекомендовано, но не было выполнено).
Н.Новгород, 2012 г.
Параллельные численные методы.
6 из 83
Типы данных…

Как правило, современные вычислительные системы
предоставляют два класса численных типов данных:
– класс, члены которого аппроксимируют множество
целых чисел;
– класс, члены которого аппроксимируют множество
действительных чисел.
Н.Новгород, 2012 г.
Параллельные численные методы.
7 из 83
Типы данных



Множества значений численных типов не соответствуют
множествам чисел, которые представляют эти типы, а
семантика элементарных операций не соответствует
семантике их математических аналогов.
Эти несоответствия фундаментальны, поскольку
множество чисел бесконечно, тогда как память любого
компьютера может иметь лишь конечное число состояний.
Поэтому значениями численных типов может быть лишь
какое-то конечное подмножество чисел. Разумеется, это
подмножество будет незамкнуто относительно
математических операций, поэтому элементарные
численные операции не могут всегда выдавать точный
математический результат.
Н.Новгород, 2012 г.
Параллельные численные методы.
8 из 83
Представление и свойства чисел с
плавающей запятой
Н.Новгород, 2012 г.
Параллельные численные методы.
9 из 83
Числа с фиксированной запятой…


Арифметика с фиксированной запятой (fixed point) —
альтернативный подход к арифметике с дробями,
меняющий точность на эффективность.
Замечание: дословно fixed point — это фиксированная
точка; но при этом имеется в виду разделитель целой и
дробной части, поэтому в русском языке используется
слово «запятая». Аналогично для термина «плавающая
запятая» (floating point).
Н.Новгород, 2012 г.
Параллельные численные методы.
10 из 83
Числа с фиксированной запятой…


Тип с фиксированной запятой — это просто
традиционный целочисленный тип длины n с
модифицированной интерпретацией — каждое значение
типа считается разделённым на 10p, где p — параметр,
означающий число знаков после запятой.
Таким образом, считается, что во множество значений
такого типа входят все десятичные дроби в определённом
интервале с не более чем p знаками после запятой.
– Например, для знакового типа длины 16 бит и ,
считается, что представлению [00110000 00111001]
соответствует число не 12345, а 123,45.
Н.Новгород, 2012 г.
Параллельные численные методы.
11 из 83
Числа с фиксированной запятой…



Операции сложения, вычитания, взятия
противоположного, сравнения для таких чисел — это
просто соответствующие целочисленные операции.
Целочисленным операциям умножения и деления нацело
соответствуют умножение и деление дроби на целое
число; однако деление будет в общем случае
произведено неточно (в какую сторону будет округлён
результат, зависит от семантики целочисленного
деления).
Кроме того, можно умножить две дроби, если произвести
целочисленное умножение и разделить результат на 10p;
разумеется, такой результат тоже будет в общем случае
неточным.
Н.Новгород, 2012 г.
Параллельные численные методы.
12 из 83
Числа с фиксированной запятой…



Недостатком чисел с фиксированной запятой является то,
что умножение и деление выполняются с ошибками,
которые не связаны с выходом за представимый
диапазон.
Преимуществом является то, что операции с ними легко
реализовать, и они работают почти так же эффективно,
как и соответствующие операции над целыми числами.
Числа с фиксированной запятой можно использовать
тогда, когда число необходимых знаков после запятой
фиксировано (например, при вычислениях, связанных с
денежными суммами), а также как грубую альтернативу
числам с плавающей запятой (о которых речь пойдёт
дальше) на системах, где нет их аппаратной поддержки.
Н.Новгород, 2012 г.
Параллельные численные методы.
13 из 83
Числа с фиксированной запятой


Помимо того, что некоторые операции выполняются
неточно, у чисел с фиксированной запятой есть ещё один
существенный недостаток: число значащих цифр числа,
которые можно представить в типе данных, зависит от
абсолютной величины этого числа.
Например, для предыдущего примера типа с двумя
знаками после запятой, у числа 123,45 хранится 5
значащих цифр, тогда как у числа 0,12 только две. Это
означает, что чем меньше числа, тем больше
относительная ошибка для тех операций, которые
выполняются неточно. При этом нулевые биты, которые
находятся в представлении числа слева, расходуются
практически впустую.
Н.Новгород, 2012 г.
Параллельные численные методы.
14 из 83
Числа с плавающей запятой



Для работы с действительными числами в современных
вычислительных системах используется арифметика с
плавающей запятой (floating point).
Основная идея заключается в том, что почти для каждого
числа хранится одинаковое количество значащих цифр, и
дополнительно хранится информация о его абсолютной
величине (т.е. о местоположении запятой).
На числа с плавающей запятой существует формальный
стандарт, который реализован в том или ином объёме
практически повсеместно:
– IEEE 754-1985: IEEE Standard for Binary Floating-Point
Arithmetic.
– IEEE 754-2008: IEEE Standard for Floating-Point Arithmetic.
Н.Новгород, 2012 г.
Параллельные численные методы.
15 из 83
Стандарты



Стандарт распространяется на вычислительную систему
в целом: для его эффективной реализации нужны
поддержка со стороны языка программирования,
компилятора и процессора.
Реализации второго, действующего, издания, пока не
распространены; даже первое издание не всегда
реализуется полностью.
Тем не менее, в большинстве случаев реализация
арифметики с плавающей запятой в вычислительной
системе хотя бы частично основана на этом стандарте.
Поэтому далее описание типов и операций с плавающей
запятой будет соответствовать требованиям на эти
сущности, изложенным в последнем издании IEEE 754.
Н.Новгород, 2012 г.
Параллельные численные методы.
16 из 83
Типы с плавающей запятой…
Каждый тип с плавающей запятой характеризуется своим
размером k, который должен быть кратен 32 битам. От
него зависят несколько производных параметров:
– Ширина поля порядка w.
– Ширина поля мантиссы t.
– Число хранимых значащих цифр p = t + 1.
– Максимальный порядок emax = 2w-1 - 1.
– Минимальный порядок emin = 1 – emax = 2 - 2w-1.
(для десятичных дробей здесь и далее в качестве
основания использовалось бы не 2, а 10)

Н.Новгород, 2012 г.
Параллельные численные методы.
17 из 83
Типы с плавающей запятой




Множество значений определяется по этим параметрам и
состоит из следующих элементов:
Все числа вида ±2e × m, где e — любое целое число на
отрезке [emin, emax], а m — любое двоичное число вида m
= d0,d1d2…dp-1. Многие числа можно представить в таком
виде несколькими способами, во множество значений все
они входят по одному разу, за исключением нуля. Нуль
входит во множество значений ровно два раза: эти
значения называются +0 и -0.
Два специальных значения, +∞ и -∞.
Два специальных значения NaN (not a number, «не число»),
sNaN (signaling NaN, сигнальный NaN) и qNaN (quiet NaN,
тихий NaN), обозначающие ошибочные ситуации.
Н.Новгород, 2012 г.
Параллельные численные методы.
18 из 83
Нормальные и субнормальные числа



Числа, абсолютная величина которых больше или равна
2emin называются нормальными (normal). Остальные, за
исключением двух нулей, называются субнормальными
(subnormal). Нули не считаются ни нормальными, ни
субнормальными.
Субнормальные числа подобны числам с фиксированной
запятой тем, что чем меньше модуль числа, тем меньше
значащих цифр для него хранится, а значит вычисления,
в результате которых получаются субнормальные числа,
выполняются с меньшей точностью, чем p.
В первом издании стандарта субнормальные числа
назывались денормализованными, и этот термин тоже
достаточно широко распространён.
Н.Новгород, 2012 г.
Параллельные численные методы.
19 из 83
Параметры типов


В таблице приведены имена и параметры типов,
определяемых стандартом.
Стандарт также описывает правила, по которым следует
определять параметры для типов длиннее 128 битов, но
здесь они не приведены, поскольку такие типы мало
распространены.
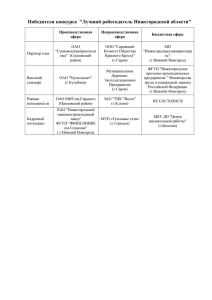
Тип
k
w
t
p
emin
emax
binary16
16
5
10
11
-14
15
binary32
32
8
23
24
-126
127
binary64
64
11
52
53
-1022
1023
binary128
128
15
112 113
-16382
16383
Н.Новгород, 2012 г.
Параллельные численные методы.
20 из 83
Граничные значения типов

В таблице приведены границы типов с плавающей
запятой.
Тип
Конечный
максимум (
2emax 1,11 1 )
Положительный
нормальный
минимум ( 2emin )
Положительный
минимум
( 2emin  0,00 1 )
binary16
 7 104
 6  10 5
 6  10 8
binary32
 3 1038
 11038
 11045
binary64
 2  10308
 2 10308
 5  10324
binary128
 1104932
 3 104932
 6 104966
Н.Новгород, 2012 г.
Параллельные численные методы.
21 из 83
Множество значений



Хотя числа с плавающей запятой предназначены для
аппроксимации действительных чисел, множество
представимых значений не является ни подмножеством,
ни надмножеством ℝ.
Специальные значения позволяют производить такие
операции, которые математически не определены на
множестве действительных чисел; стандарт однозначно
определяет результат для всех операций и для всех
параметров.
Все числа, входящие во множество значений, на самом
деле рациональные.
Н.Новгород, 2012 г.
Параллельные численные методы.
22 из 83
Представление чисел c плавающей запятой

Представление каждого типа с плавающей запятой
состоит из трёх полей:
– Знака, размером в 1 бит;
– Порядка, размером в w бит;
– Мантиссы, размером в t бит.
Н.Новгород, 2012 г.
Параллельные численные методы.
23 из 83
Представление бесконечностей
Для значений +∞ и -∞, поле знака равно 0 или 1
соответственно, поле порядка заполнено единицами, а
поле мантиссы заполнено нулями:
+∞  [0 11111 0000000000]
-∞  [1 11111 0000000000]
(здесь и далее для краткости примеры для типа binary16).

Н.Новгород, 2012 г.
Параллельные численные методы.
24 из 83
Представление NaN




Для значений sNaN и qNaN поле порядка заполнено
единицами, а поле мантиссы содержит хотя бы один
единичный бит.
Поле знака и поле мантиссы могут быть заполнены
произвольно (за исключением ограничения в один
единичный бит для мантиссы); независимо от их
содержимого значением является sNaN или qNaN.
Различие между представлениями тихого и сигнального
NaN не фиксировано, но рекомендуется, чтобы у тихих
NaN самый левый бит поля мантиссы был равен единице,
а у сигнальных — нулю.
sNaN / qNaN  [? 11111 ??????????]
Н.Новгород, 2012 г.
Параллельные численные методы.
25 из 83
Представление нормальных чисел



Нормальные числа сначала представляются в виде ±2e ×
1,d1d2…dt. Это всегда можно сделать, так из ограничения
по модулю следует, что среди цифр найдётся хотя бы
одна единица.
Поле знака равно 0, если число положительно и 1, если
отрицательно; поле порядка является представлением
числа e + emax как значения w-битного беззнакового
целочисленного типа; а биты мантиссы равны d1, d2, …, dt
слева направо.
Например, 123 = 11110112 = 26 × 1,1110112  [0 10101
1110110000].
Н.Новгород, 2012 г.
Параллельные численные методы.
26 из 83
Представление субнормальных чисел и нулей


Субнормальные числа имеют вид ±2emin × 0,d1d2…dt (это
непосредственно следует из определения множества
представимых значений). Поле знака и поле мантиссы
для них определяются так же, как и для нормальных
чисел; поле порядка заполнено нулями.
– Например, -0,00003814697265625 =
-0,000000000000001012 = -2-14 × 0,1012  [1 00000
1010000000].
Числа +0 и -0 представляются тем же способом, что и
субнормальные числа.
– +0 = 2-14 × 0,0…  [0 00000 0000000000]
– -0 = -2-14 × 0,0…  [1 00000 0000000000]
Н.Новгород, 2012 г.
Параллельные численные методы.
27 из 83
Определение класса числа по представлению


Каждая w-битная строка является представлением какоголибо значения.
Определить класс значения можно следующим образом:
– Если поле порядка состоит только из единичных битов,
то это бесконечность (если поле мантиссы состоит
только из нулевых битов) или NaN (в противном
случае).
– Если поле порядка состоит только из нулевых битов, то
это ноль (если поле мантиссы состоит только из
нулевых битов) или субнормальное число (в противном
случае).
– Иначе, это нормальное число.
Н.Новгород, 2012 г.
Параллельные численные методы.
28 из 83
Свойства представления


Для чисел одного знака и бесконечности того же знака,
совпадает математический и лексикографический
порядок, т.е. сравнение двух представлений как целых
чисел выдаёт либо правильный результат (для
положительного знака), либо противоположный (для
отрицательного).
– Это свойство обеспечивается, в частности, тем, что к
порядку при представлении прибавляется emax,
вследствие чего и отрицательные, и положительные
порядки упорядочены лексикографически.
Представление, состоящее только из нулевых битов,
соответствует значению +0; состоящее только из
единичных — одному из значений NaN.
Н.Новгород, 2012 г.
Параллельные численные методы.
29 из 83
Операции над числами с плавающей запятой




IEEE 754 определяет набор обязательных операций,
которые должны поддерживаться для типов с плавающей
запятой, и набор рекомендуемых.
Соответствие этих операций конструкциям языка
определяется вычислительной системой — обычно они
отображаются в операторы и функции.
Набор обязательных операций включает
арифметические, операции сравнения, конвертирования,
проверки принадлежности классам, округление и
некоторые другие.
Также стандарт рекомендует поддержку вычисления
элементарных функций.
Н.Новгород, 2012 г.
Параллельные численные методы.
30 из 83
Требования к точности



В случае, когда аргументы являются конечными и
математический результат операции определен, должен
быть возвращен математический результат, округленный
до представимого типом значения.
В противном случае результат зависит от конкретной
операции. Как правило, бесконечности ведут себя
интуитивно ясным способом.
– Например, деление конечного числа на 0, логарифм
нуля, сумма бесконечности и конечного числа дают
бесконечность правильного знака.
Если бесконечность не подходит в качестве «интуитивно
правильного» результата, возвращается NaN.
– Например, при делении 0 на 0.
Н.Новгород, 2012 г.
Параллельные численные методы.
31 из 83
Округление


Округление ставит любому действительному числу одно
из ближайших к нему представимых значений типа. Какое
именно, зависит от текущего режима округления (rounding
mode). Стандарт определяет пять таких режимов.
roundTiesToEven (к чётному в случае ничьи) —
выбирается самое близкое значение; если таких два,
выбирается то, у которого младшая цифра мантиссы
равна нулю (т.е. чётное). Это требуемый режим по
умолчанию. Он близок к математической концепции
округления; правило о предпочтении чётных чисел
предназначено смягчить систематическую ошибку
округления при выполнении большого числа операций.
Н.Новгород, 2012 г.
Параллельные численные методы.
32 из 83
Режимы округления




roundTiesToAway (в сторону, противоположную нулю, в
случае ничьи) — выбирается самое близкое значение; если
таких два, выбирается большее по абсолютной величине.
Этот режим эквивалентен математическому округлению.
roundTowardPositive (в положительном направлении) —
выбирается ближайшее значение из тех, которые больше
или равны числу. Это может быть +∞.
roundTowardNegative (в отрицательном направлении) —
выбирается ближайшее значение из тех, которые меньше
или равны числу. Это может быть -∞.
roundTowardZero (в направлении нуля) — выбирается
ближайшее значение из тех, которые меньше или равны
числу по абсолютной величине.
Н.Новгород, 2012 г.
Параллельные численные методы.
33 из 83
Округление и точность…
Как округление работает в операциях, можно видеть на
следующем примере:
1,10101010102 * 1,01010101012 =
1,0001110001|000011100102  1,00011100012
 На каждую операцию производится ровно одно
округление.
 Этим мотивировано существование операций, которые,
на первый взгляд, только комбинируют несколько других.
Например, результат операции fusedMultiplyAdd(x, y, z)
может быть не равен результату операций
addition(multiplication(x, y), z).

Н.Новгород, 2012 г.
Параллельные численные методы.
34 из 83
Округление и точность
Это хорошо видно на следующем примере:
x = 1,10101010102
y = 1,01010101012
z = -1,00011100012
(1,10101010102 * 1,01010101012) + -1,00011100012 
 1,00011100012 + -1,00011100012  02
1,10101010102 * 1,01010101012 + -1,00011100012 =
= 0,0000000000000011100102 = 0,11100100002 × 2−14
(округление не требуется)

Н.Новгород, 2012 г.
Параллельные численные методы.
35 из 83
Исключения…
Результат однозначно определён для любых операций и
операндов.
 Однако для упрощения обнаружения и восстановления
после нежелательных операций, стандарт
предусматривает механизм исключений.
 Определено пять исключительных ситуаций, каждой
соответствует статусный флаг.
 Обработчики по умолчанию устанавливают эти флаги и
возвращают результат в соответствии со стандартом.
 Приложение может обрабатывать исключительные
ситуации, работая с флагами (для этого предусмотрены
специальные операции) или заменяя обработчик
исключений по умолчанию.

Н.Новгород, 2012 г.
Параллельные численные методы.
36 из 83
Исключения…


Некорректная операция (invalid operation). Вызывается,
когда у операции нет полезного результата (т.е. конечного
числа или бесконечности). Деление нуля на ноль
является примером такой операции. Кроме того, это
исключение вызывается в (почти) любой операции, среди
аргументов которой есть сигнальный NaN. Обработчик по
умолчанию поднимает соответствующий флаг и
возвращает в качестве результата тихий NaN.
Деление на ноль (division by zero). Вызывается, когда у
операции над конечными операндами в качестве
результата получается бесконечность. Обработчик по
умолчанию поднимает соответствующий флаг и
возвращает в качестве результата бесконечность нужного
знака.
Н.Новгород, 2012 г.
Параллельные численные методы.
37 из 83
Исключения…

Переполнение (overflow). Вызывается, когда результат
операции конечен, но слишком велик для представления
(по абсолютной величине). Обработчик по умолчанию
поднимает соответствующий флаг, вызывает
дополнительно исключение «неточность» и возвращает
корректно округлённый результат (в зависимости от
режима округления это может быть конечное число или
бесконечность).
Н.Новгород, 2012 г.
Параллельные численные методы.
38 из 83
Исключения…

Исчезновение порядка (underflow). Вызывается, когда
результат операции не равен в точности нулю, но строго
меньше 2emin по абсолютной величине. Это означает, что
результат является субнормальным числом, либо меньше
минимального представимого субнормального числа.
Если математический результат принадлежит множеству
значений типа результата, обработчик по умолчанию
возвращает этот результат и не поднимает
соответствующий исключению статусный флаг. В
противном случае поднимается флаг, дополнительно
вызывается исключение «неточность» и возвращается
корректно округлённый результат.
Н.Новгород, 2012 г.
Параллельные численные методы.
39 из 83
Исключения

Неточность (inexact). Вызывается, когда математический
результат операции не равен округлённому. Обработчик
по умолчанию поднимает соответствующий статусный
флаг и возвращает корректно округлённый результат. Это
исключение необязательно для рекомендуемых
операций.
Н.Новгород, 2012 г.
Параллельные численные методы.
40 из 83
Причины ошибок…


Работа с действительными числами (в виде чисел с
плавающей запятой) в устроена значительно сложнее,
чем работа с целыми:
– Усложнение множества допустимых значений:
несколько подмножеств с разными свойствами.
– Семантика операций: к двум потенциально
нежелательным ситуациям из целочисленной
арифметики (делению на ноль и переполнению)
добавились ещё три (некорректная операция,
исчезновение порядка и неточность).
Это означает, что программисту, особенно не изучавшему
арифметику с плавающей запятой в деталях, сложнее
предугадать результат программы и обнаружить ошибку.
Н.Новгород, 2012 г.
Параллельные численные методы.
41 из 83
Причины ошибок…



Несмотря на то, что целью этого усложнения является как
можно более точное отражение математических
конструкций, арифметика с плавающей запятой не
идентична математической арифметике действительных
чисел.
Это естественно — память компьютера не может содержать
в себе бесконечное число цифр любого иррационального
числа — но это всегда необходимо иметь в виду.
Ошибки, связанные с числами с плавающей запятой, можно
условно разделить на две группы — связанные с
ограниченностью множества значений и связанные с
нематематичной семантикой операций (условность в том,
что второе в конечном итоге вызывается первым).
Н.Новгород, 2012 г.
Параллельные численные методы.
42 из 83
Неточность при суммировании…




Классический пример ситуации, в которой неточность
играет роль — сложение элементов массива.
Если все элементы массива имеют одинаковый знак и
примерно одинаковый порядок, и сложение происходит
последовательно, то порядок частичных сумм постепенно
увеличивается.
Это приводит к тому, что часть битов мантиссы элементов
с правого конца массива при сложении пропадает, хотя те
же биты элементов с левого конца учитываются.
Это означает, что правые элементы дают менее
правильный вклад в сумму, чем левые, и хотя каждое
сложение рассчитано с максимально возможной
точностью, для всей суммы это неверно.
Н.Новгород, 2012 г.
Параллельные численные методы.
43 из 83
Неточность при суммировании

Для повышения точности суммирования существует
несколько техник, включая переупорядочивание
элементов (для элементов разного порядка),
суммирование с компенсацией, и временное
использование типа большей точности.
Н.Новгород, 2012 г.
Параллельные численные методы.
44 из 83
Катастрофическая потеря точности…




Иногда в результате серии операций может получаться
полностью неверный результат.
Ранее был рассмотрен пример с FMA: при вычислении
выражения 1,10101010102 * 1,01010101012 + -1,00011100012
как двух последовательных операций в качестве результата
был получен ноль, хотя математический результат равен
0,1110012, то есть итоговая ошибка составила 100%.
При этом при умножении была допущена минимально
возможная ошибка, а при сложении вообще нулевая!
Причина ошибки в том, что большое количество старших
бит в процессе вычислений были сокращены и
значительная часть существенных для результата битов
была отброшена.
Н.Новгород, 2012 г.
Параллельные численные методы.
45 из 83
Катастрофическая потеря точности…



Этот эффект называется катастрофической потерей
точности.
Подобная ситуация также может возникнуть в случае
подсчёта выражений вида ex - 1 (при x, близком к нулю),
sqrt(1 + x2) - x (при больших x), и других, как
последовательности операций.
Действия по исправлению ошибки зависит от
обстоятельств. Например, как уже было показано ранее,
операция fusedMultiplyAdd решает проблему в
предыдущем примере.
Н.Новгород, 2012 г.
Параллельные численные методы.
46 из 83
Катастрофическая потеря точности


Для вычисления выражения ex – 1 стандартом
предусмотрена специальная операция expm1,
вычисляющее его с максимальной точностью. Подобное
вычисление можно также реализовать с помощью ручного
суммирования ряда Тейлора с предварительным
сокращением 1.
Для выражения sqrt(1 + x2) – x можно применить
следующее алгебраическое преобразование:
Н.Новгород, 2012 г.
Параллельные численные методы.
47 из 83
Рекомендации…


Ни ошибки в представлении, ни неточности операций не
являются фатальными и не означают наверняка, что
результат вычислений окажется бесполезным.
Тем не менее, их наличие означает, что
– результат не будет совпадать в точности с
математическим результатом;
– результаты математически эквивалентных выражений
могут не совпадать;
– точное сравнение на равенство при работе с
плавающей точкой редко бывает полезно (обычно
проверяется, что числа достаточно близко).
Н.Новгород, 2012 г.
Параллельные численные методы.
48 из 83
Рекомендации

Если в результате вычислений получен неправильный
результат, это может означать, что используемый тип не
способен обеспечить нужную точность — но, с другой
стороны, иногда точность можно улучшить, изменив
вычислительную схему преобразованиями.
Н.Новгород, 2012 г.
Параллельные численные методы.
49 из 83
Особенности реализаций
Н.Новгород, 2012 г.
Параллельные численные методы.
50 из 83
Введение
Поддержку вычислительной системой стандарта IEEE-754
можно разложить на три компоненты:
– поддержка на аппаратном уровне
– поддержка языком программирования
– поддержка транслятором языка
 Мы рассмотрим пример реализации каждой из этих
компонент.

Н.Новгород, 2012 г.
Параллельные численные методы.
51 из 83
Архитектура x86-64
x86-64 (также AMD64, Intel 64, EM64T, x64) — 64-битная
архитектура системы команд процессоров, выпускаемых в
основном компаниями Intel и AMD.
 В настоящее время используется на значительной части
серверов и большинстве домашних компьютеров.
 Является расширением старой 32-битной архитектуры
x86 (IA-32), и обратно совместима с ней.
 Поддерживает по меньшей мере два способа работы с
плавающей запятой.

Н.Новгород, 2012 г.
Параллельные численные методы.
52 из 83
x87…


x87 — название старой архитектуры сопроцессоров для
работы с числами с плавающей запятой; сейчас
обозначает функциональность x86-процессоров,
повторяющую эту архитектуру.
Предоставляет 8 регистров (fpr0-fpr7) особого формата:
– Общая длина представления k = 80 бит.
– Длина поля мантиссы t = 63 бита.
– Длина поля порядка w = 15 бит.
– Оставшийся бит (Integer bit) содержит цифру слева от
запятой, и должен быть согласован с остальными
полями.
Н.Новгород, 2012 г.
Параллельные численные методы.
53 из 83
x87




Не считая лишнего поля, формат x87 устроен согласно
стандарту.
sNaN отличается от qNaN рекомендуемым образом — у
qNaN установлен старший бит мантиссы.
Инструкции x87 позволяют аппаратно выполнять
большинство обязательных операций и часть
рекомендуемых.
Кроме того, x87 предоставляет средства для изменения
нескольких аспектов своей работы…
Н.Новгород, 2012 г.
Параллельные численные методы.
54 из 83
x87 – точность





Формат по умолчанию имеет точность больше, чем у
стандартных форматов binary32 и binary64.
С одной стороны, это означает, что вычисления
производятся точнее, чем с этими форматами.
С другой стороны, программа, которая работала с x87
может перестать возвращать корректный результат на
архитектурах, использующих стандартные форматы.
Для повышения предсказуемости x87 позволяет
уменьшить используемую длину поля мантиссы до 23 или
52 бит, что соответствует binary32 и binary64.
Впрочем, длина поля порядка остаётся неизменной, а
значит, совместимость достигается не полная.
Н.Новгород, 2012 г.
Параллельные численные методы.
55 из 83
x87 – округление и исключения



x87 позволяет выбрать один из четырёх стандартных
способов округления — к ближайшему (чётному в случае
ничьи), вниз, вверх и к нулю.
x87 поддерживает 5 стандартных исключений, а также
шестое, которое генерируется, если на вход операции
поступает субнормальное число.
Каждое исключение может быть маскировано
(выполняется стандартная обработка по умолчанию) и
немаскировано (в этом случае генерируется
процессорное исключение). Обработка по умолчанию
устанавливает соответствующий исключению флаг в
статусном регистре FSW.
Н.Новгород, 2012 г.
Параллельные численные методы.
56 из 83
3DNow!




3DNow! — хронологически второй способ осуществлять
операции с плавающей запятой.
Работает с 64-битными регистрами mmx0-mmx7, которые
вмещают в себя два числа в формате binary32.
Эти регистры перекрывают x87-регистры fpr0-fpr7,
поэтому нельзя одновременно использовать x87 и
3DNow!
3DNow! был реализован только на процессорах AMD и
мало популярен; AMD в настоящий момент советует
использовать вместо него SSE.
Н.Новгород, 2012 г.
Параллельные численные методы.
57 из 83
SSE

SSE (Streaming SIMD Extensions), SSE2, SSE3, SSSE3,
SSE4 — семейство расширений x86/x86-64 для
поддержки векторных операций.
 Предоставляет 16 128-битных регистров XMM0-XMM15.
 Каждый может содержать 2 значения формата binary64
или 4 — формата binary32 (а также целые числа в ряде
форматов).
 Инструкции позволяют работать как со всеми значениями
регистра, так и с одним.
 В отличие от x87, поддерживаются только обязательные
операции.
Н.Новгород, 2012 г.
Параллельные численные методы.
58 из 83
SSE и x87
SSE можно использовать как замену x87.
 Компиляторы под x86-64 часто так и делают, поскольку
SSE и SSE2 поддерживаются во всех процессорах x86-64.
 В отличие от x87, SSE работает со стандартными
форматами, повышая предсказуемость.
 SSE поддерживает те же четыре режима округления и те
же шесть исключений, что и x87.
 Кроме того, поддерживаются опции, позволяющие
отключить поддержку субнормальных чисел. Как правило,
операции с субнормальными числами выполняются
медленнее, чем над нормальными и нулями, и иногда без
них можно обойтись.

Н.Новгород, 2012 г.
Параллельные численные методы.
59 из 83
x86-64 – будущее

(На момент написания) Intel и AMD внедряют в свои
процессоры дополнительные расширения для SSE:
– AVX (Advanced Vector Extensions):
• новые 256-битные регистры YMM0-YMM15, перекрывающие
XMM-регистры;
• инструкции для работы с ними;
– F16C — конвертирование значений в/из формата
binary16. Операции для этого формата всё ещё не
поддерживаются.
– FMA3, FMA4 — операция fusedMultiplyAdd. Раньше эта
операция не была реализована аппаратно, так как
появилась только во втором издании IEEE 754.
Реализации Intel и AMD похожи, но несовместимы.
Н.Новгород, 2012 г.
Параллельные численные методы.
60 из 83
C
C — один из самых популярных языков для написания
вычислительных программ.
 Определяется стандартом ISO/IEC:
– ISO/IEC 9899:1990 (он же С90 или С89)
– ISO/IEC 9899:1999 (он же C99)
 С90 реализован повсеместно, С99 не очень.
 Многие из нововведений C99 имеют отношение к
арифметике с плавающей запятой.

Н.Новгород, 2012 г.
Параллельные численные методы.
61 из 83
C и IEEE 754



Cтандарт C не требует, чтобы действительные типы и
операции с ними удовлетворяли IEEE 754. Для
реализаций, где это так (а обычно это так), стандарт
определяет набор дополнительных требований.
На момент публикации C99 существовало только первое
издание IEEE 754, поэтому часть операций из второго
издания в C отсутствует.
Конкретные реализации C часто добавляют свои
расширения, которые могут иметь отношение к
арифметике с плавающей запятой.
Н.Новгород, 2012 г.
Параллельные численные методы.
62 из 83
С – типы

C предоставляет три так называемых вещественных типа
с плавающей запятой:
– float — binary32;
– double — binary64;
– long double — может быть эквивалентен binary64 или
быть шире;
• Например, 80-битный тип x87.
Н.Новгород, 2012 г.
Параллельные численные методы.
63 из 83
C – константы

Способы задания вещественных констант:
– В десятичном виде:
• 1.5
2
• 1.5e2  1.5 10
– В шестнадцатеричном видеC99:
3
• 0x1.ab3p-3  1.ab316  2
• Можно точно и компактно записать любое представимое число.
Тип константы по умолчанию — double. Для float
используется суффикс f/F; для long double — l/L.
 Для специальных значений есть макросы в <math.h>:
HUGE_VAL (+∞), INFINITYC99 (+∞) и NANC99 (qNaN).
Стандарт не требует поддерживать sNaN.

Н.Новгород, 2012 г.
Параллельные численные методы.
64 из 83
C – функции
Обязательные операции IEEE 754 реализуются
операторами языка, а также функциями и макросами из
стандартной библиотеки:
– <math.h> — математические операции;
– <stdio.h>, <stdlib.h> — преобразования в/из строк;
– <fenv.h> — манипуляции окружением;
 В C99 почти все такие функции продублированы для всех
трёх вещественных типов, например fabsf (float) – fabs
(double) – fabsl (long double).
 Часть рекомендуемых операций доступна в виде функций
из <math.h>. C, в отличие от IEEE 754, не требует считать
эти функции с максимально возможной точностью.

Н.Новгород, 2012 г.
Параллельные численные методы.
65 из 83
C – окружение



Текущий режим округления можно установить/определить
с помощью функций <fenv.h> fesetroundC99 и fegetroundC99
(кроме режима округления к нулю в случае ничьи,
который не поддерживается).
Для исключений стандартом поддерживается только
обработка по умолчанию (с флагами исключений можно
работать с помощью функций из <fenv.h>), но
предполагается, что реализации могут добавлять свои
способы обработки.
Программа, которая обращается к функциям из <fenv.h>
должна включать директиву #pragma STDC
FENV_ACCESS ON C99, в противном случае поведение
программы не определено.
Н.Новгород, 2012 г.
Параллельные численные методы.
66 из 83
C – промежуточные значения…



C позволяет производить вычисления с плавающей
точкой в формате большей точности, чем тип операндов.
Результат должен приводиться к конкретному типу только
при записи в переменную этого типа.
Цель этого разрешения в том, чтобы реализации могли
использовать самый эффективный способ выполнения
операций, дающий заданную или лучшую точность.
Например, компилятору можно использовать для
промежуточных результатов расширенный тип x87, не
выгружая каждый промежуточный результат в память для
приведения типа.
Н.Новгород, 2012 г.
Параллельные численные методы.
67 из 83
C – промежуточные значения…

Макрос <float.h> FLT_EVAL_METHODC99 указывает, в
каком формате представляются промежуточные
значения:
– 0 — в том же, что и аргументы;
– 1 — double для аргументов float и double; long double
для long double;
– 2 — long double;
– другое значение — какой-то другой вариант.
Н.Новгород, 2012 г.
Параллельные численные методы.
68 из 83
C – промежуточные значения
Таким образом, значения двух выражений могут не
совпадать, даже если они эквивалентны:
 float f = 1.0f / 3.0f;
– Результат деления записывается в переменную,
значит, округляется до типа binary32.
 bool b = f == 1.0f / 3.0f;
– Результат деления используется только как
промежуточный результат и может находиться в
формате, зависящем от реализации.
– b может быть как true, так и false.

Н.Новгород, 2012 г.
Параллельные численные методы.
69 из 83
С – сжатие выражений




С разрешает реализациям посчитать сложное выражение
как одну операцию, то есть вычислить его математически
точное значение и один раз округлить его для
представления в целевом формате.
Например, заменить последовательность из умножения и
сложения на операцию fusedMultiplyAdd.
Можно запретить сжимать выражения с помощью
директивы #pragma STDC FP_CONTRACT OFFC99.
В отсутствие этой директивы компилятор не обязан
сжимать все выражения, которые способен. Если
корректность результата зависит от использования
сложной операции, её нужно использовать явно (в
примере — функцией fmaC99).
Н.Новгород, 2012 г.
Параллельные численные методы.
70 из 83
С – оптимизации



Результат работы программы могут изменить возможные
оптимизации.
Или нет… C разрешает только преобразования
программы, не влияющие на её поведение.
– x * 0.5 ≡ x / 2.0
– x + 0 ≢ x (если x равен -0, x + 0 равно +0)
– x == x ≢ true (NaN не равен самому себе)
– (a + b) + c ≢ a + (b + c)
Но компиляторы для обеспечения скорости работы могут
предоставлять режимы агрессивной оптимизации,
игнорирующие эти ограничения. Иногда даже по
умолчанию.
Н.Новгород, 2012 г.
Параллельные численные методы.
71 из 83
Компиляторы

Мы рассмотрим поддержку арифметики с плавающей
запятой в двух популярных компиляторах:
– Компилятор Microsoft (MC), который входит в состав
Microsoft Visual Studio 2008.
• Создаёт программы под Windows для архитектур x86 и x86-64
(а также IA-64).
• Поддерживает C90, но некоторые расширения повторяют
часть функциональности C99.
– Компилятор Intel (IC), который входит в состав Intel
Composer XE 2011.
• Создаёт программы под Windows, Linux, Mac OS X для тех же
архитектур (мы рассмотрим Windows-версию, которая
совместима с MC).
• Поддерживает большую часть C99.
Н.Новгород, 2012 г.
Параллельные численные методы.
72 из 83
Компиляторы – наборы инструкций
MC поддерживает x87, SSE и SSE2.
– При компиляции под x86 используется только x87.
SSE/SSE2 можно включить с помощью опции /arch.
– При компиляции под x86-64 SSE и SSE2 включены
сразу и не выключаются.
 IC также поддерживает SSE3, SSSE3, SSE4.1, SSE4.2 и
AVX.
– По умолчанию включены SSE и SSE2. Остальные
наборы включаются опциями /arch и /Qx.
 Опции разрешают использовать конкретный набор
команд, а не заставляют.

Н.Новгород, 2012 г.
Параллельные численные методы.
73 из 83
Компиляторы – векторизация…



В отличие от MC, IC умеет автоматически применять
векторные инструкции SSE, чем зачастую обеспечивает
скомпилированным программам большую
производительность, чем MC.
Если вы используете MC, или вам кажется, что вы можете
использовать векторные инструкции лучше, чем это
делает IC, но при этом вы не хотите писать код на
ассемблере, то вы можете векторизовать свой код
вручную с помощью интринсик (intrinsics).
Интринсики — это типы данных и функции,
предоставляемые рассматриваемыми компиляторами,
которые напрямую, или почти напрямую, соответствуют
регистрам и инструкциям из семейства SSE.
Н.Новгород, 2012 г.
Параллельные численные методы.
74 из 83
Компиляторы – векторизация

Например, следующая функция возвращает сумму
квадратов элементов массива:
#include <xmmintrin.h>
float sumsquare_intrinsics(const float * a, int n)
{
__m128 sum, element;
int i;
float result[4];
sum = _mm_setzero_ps();
for (i = 0; i < n; i += 4)
{
element = _mm_load_ps(a + i);
sum = _mm_add_ps(sum,
_mm_mul_ps(element, element));
}
_mm_store_ps(result, sum);
return result[0] + result[1] + result[2] + result[3];
}
Н.Новгород, 2012 г.
Параллельные численные методы.
75 из 83
Компиляторы – режимы


В обоих компиляторах есть опция /fp, которая позволяет
менять семантику работы с плавающей запятой.
Значения этой опции делятся на три группы, внутри
каждой из которых можно выбрать ровно один из
вариантов:
– precise, fast, strict;
– source, double, extended (только в IC);
– except, except-;
Последнюю группу мы рассмотрим в разделе об
исключениях.
Н.Новгород, 2012 г.
Параллельные численные методы.
76 из 83
Компиляторы – управление оптимизацией…


Группа precise, fast, strict управляет тем, какие
оптимизации разрешено выполнять компилятору.
/fp:precise означает, что компилятору разрешается
выполнять только оптимизации, не изменяющие
результат вычислений. Это означает, что выражения
будут выполняться «как написано», и значит, программист
может пользоваться свойствами арифметики с
плавающей запятой.
Н.Новгород, 2012 г.
Параллельные численные методы.
77 из 83
Компиляторы – управление оптимизацией…
/fp:fast даёт компилятору разрешение оптимизировать код
с использованием математических свойств операций.
 С одной стороны, компилятору даётся большая свобода
при оптимизации, и итоговый код может получиться
быстрее.
 С другой стороны, компилятор может вносить ошибки,
связанные с несоблюдением семантики операций с
плавающей запятой.

float error(float a, float b)
{
return (a + b) - b - a;
}
Н.Новгород, 2012 г.
Параллельные численные методы.
float error(float a, float b)
{
return 0;
}
78 из 83
Компиляторы – управление оптимизацией





Автоматическая векторизация может производиться
только с /fp:fast, так как она меняет порядок операций, а
значит, и результат.
MC по умолчанию использует /fp:precise, IC — /fp:fast.
Третий вариант из этой группы, /fp:strict, эквивалентен
/fp:precise, но с отключенной директивой fp_contract и
включенной — fenv_access. Кроме того, /fp:strict также
устанавливает /fp:except.
fp_contract — аналог STDC FP_CONTRACT из C99,
разрешает/запрещает сжатие выражений.
fenv_access — аналог STDC FENV_ACCESS,
разрешает/запрещает доступ к окружению.
Н.Новгород, 2012 г.
Параллельные численные методы.
79 из 83
Компиляторы — промежуточные значения…
Группа /fp:source, double и extended определяет точность,
с которой считаются промежуточные результаты.
– source — формат результатов операций совпадает с
форматом аргументов операций.
– double — операции вычисляются в формате binary64.
– extended — операции вычисляются в расширенном 80битном формате x87.
 По умолчанию для x86 используется /fp:double, для x86-64
/fp:source.
 Заметим, что тип long double в обоих компиляторах
синонимичен double.
 Эта опция имеет смысл только в режиме /fp:strict.

Н.Новгород, 2012 г.
Параллельные численные методы.
80 из 83
Компиляторы — промежуточные значения…



Последствия выбора того или иного варианта зависят от
используемого набора команд.
/fp:extended форсирует использование x87 (в SSE нет
такого формата).
При использовании /fp:double или /fp:source с типом
double и набором инструкций x87 вычисления проводятся
не со стандартным форматом binary64, а с 80-битным
форматом x87, мантисса которого урезана до 53 бит. Это
означает, что используется более широкий диапазон
порядков, чем в binary64.
Н.Новгород, 2012 г.
Параллельные численные методы.
81 из 83
Компиляторы — промежуточные значения


Самая неудачная комбинация — это /fp:source при
использовании x87 и типа float. Регистры при этом
настроены на 53-битную мантиссу (на случай выражений
типа double). для обеспечения точности float результат
каждой операции должен быть выгружен из регистра в
память и загружен обратно. Теряется как точность, так и
производительность.
При использовании /fp:double и extended формат
промежуточных значений может не совпадать с
форматом конечных. Однако, компилятор обязан
привести промежуточное значение к конечному типу. Этих
преобразований может быть достаточно много (и они
могут замедлять работу программы), если выражений
вычисляется много, а сами они короткие.
Н.Новгород, 2012 г.
Параллельные численные методы.
82 из 83
Компиляторы – окружение…



Окружение арифметики с плавающей запятой включает в
себя следующие настройки:
– включена ли замена субнормальных чисел нулями;
– включена ли обработка исключений по умолчанию;
– текущий режим округления;
– текущая используемая ширина поля мантиссы;
Это те настройки, которые позволяют менять x87 и SSE.
Кроме того, в окружение входят флаги исключений.
Окружением можно манипулировать функцией <float.h>
_controlfp_s. Она меняет параметры одновременно x87 и
SSE, но, естественно, она не может задать те параметры,
которых кто-то из них не поддерживает (т.е. ширину
мантиссы для SSE).
Н.Новгород, 2012 г.
Параллельные численные методы.
83 из 83
Компиляторы – окружение

Если в программе читается или изменяется окружение,
она должна быть скомпилирована с директивой #pragma
fenv_access (on).
void something();
float square, cube;
square = x * x;
something();
cube = x * x * x;
printf("%f %f\n", square, cube);

Если не указать директиву, компилятор может
использовать square при вычислении cube, хотя вызов
something() мог изменить режим округления.
Н.Новгород, 2012 г.
Параллельные численные методы.
84 из 83
Компиляторы – исключения…

Изначально все исключения обрабатываются по
умолчанию — при их срабатывании устанавливается
соответствующий флаг. Эти флаги можно прочитать с
помощью функций <float.h> _statusfp и _clearfp (последняя
очищает все флаги после получения их значения).
float a[] = { 1e30f };
float result;
_clearfp();
result = sumsquare(a, 1);
printf("Result: %f\n", result);
if (_statusfp() & _SW_OVERFLOW)
puts("Overflow!");
Н.Новгород, 2012 г.
Параллельные численные методы.
85 из 83
Компиляторы – исключения…



Чтобы обработать исключение прямо в момент
возникновения, нужно сделать три вещи:
– Указать ключ компиляции /fp:except. Этот ключ
гарантирует, что исключение генерируется сразу после
того, как возникла исключительная ситуация. /fp:except
подразумевается в случае /fp:strict, и не совместим с
/fp:fast.
Отключить обработку по умолчанию для нужного
исключения с помощью _controlfp_s. Предварительно
стоит очистить соответствующий флаг, чтобы исключение
не возникло сразу же.
Обработать исключение самому с помощью предложения
__try.
Н.Новгород, 2012 г.
Параллельные численные методы.
86 из 83
Компиляторы – исключения…

Пример:
float a[] = { 1e30f };
float result;
unsigned old_control;
_clearfp();
_controlfp_s(&old_control, ~_EM_OVERFLOW, _MCW_EM);
__try
{
result = sumsquare(a, 1);
printf("Result: %f\n", result);
}
__except(1)
{
puts("Overflow!");
}
Н.Новгород, 2012 г.
Параллельные численные методы.
87 из 83
Компиляторы – исключения




Предложение __try … __except является расширением,
реализованным в MC и IC.
Это не try … catch из C++; __try работает как в C, так и в
C++.
__try работает независимо от try, и отличается
синтаксисом: в части __except указывается не тип, а
выражение, от результата которого зависит поведение
программы. См. документацию Microsoft.
Программисты на C++, которые уже используют
исключения C++, могут использовать трансляцию
исключений с плавающей запятой в исключения C++ с
помощью пользовательской функции-транслятора. См.
функцию _set_se_translator.
Н.Новгород, 2012 г.
Параллельные численные методы.
88 из 83
Компиляторы – элементарные функции


Оба компилятора реализуют полный набор элементарных
функций из заголовка <math.h> C90; в IC также входит
альтернативный заголовок <mathimf.h>, который
позволяет использовать и функции из C99.
Если опции разрешают векторизацию, IC может заменить
вызовы элементарных функций в цикле на реализации,
оперирующие непосредственно с SSE-регистрами, из
встроенной библиотеки SVML (Short Vector Math Library).
Если программисту не нравится качество векторизации,
он может использовать функции SVML вручную — они
используются аналогично простым SSE-интринсикам.
Н.Новгород, 2012 г.
Параллельные численные методы.
89 из 83
VML




Функции из SVML работают с SSE-регистрами, которые
вмещают небольшое число значений.
Если программа производит операции над большим
числом элементов, то ускорить её производительность
можно с помощью библиотеки VML (Vector Mathematical
Functions Library), которая входит в Intel Composer.
VML позволяет эффективно производить как простые
арифметические операции, так и расчёты элементарных
функций над массивами большой длины.
Кроме того, VML предлагает несколько режимов
вычислений, которые позволяют программисту выбрать
между точностью вычислений и их скоростью.
Н.Новгород, 2012 г.
Параллельные численные методы.
90 из 83
Литература…
Muller J.M., et al. Handbook of floating-point arithmetic. –
Boston: Birkhäuser, 2010.
2. Goldberg D. What every computer scientist should know
about floating-point arithmetic. // ACM Computing Surveys,
V. 23, N. 1, 1991.
3. IEEE Computer Society. IEEE Standard for Floating-Point
Arithmetic. IEEE Standard 754-2008.
4. International Organization for Standardization, International
Electrotechnical Commission. ISO/IEC 9899:1999.
Programming languages — C.
1.
Н.Новгород, 2012 г.
Параллельные численные методы.
91 из 83
Литература
5. Intel® 64 and IA-32 Architectures Software Developer
Manuals.
[http://www.intel.com/content/www/us/en/processors/architec
tures-software-developer-manuals.html].
6. Microsoft Visual C++ Floating-Point Optimization.
[http://msdn.microsoft.com/enus/library/aa289157(v=vs.71).aspx].
Курс «Параллельные численные методы»:
http://hpcc.unn.ru/?doc=491
Н.Новгород, 2012 г.
Параллельные численные методы.
92 из 83
Авторский коллектив


Бастраков Сергей Иванович,
лаборант НИЛ кафедры Математического обеспечения ЭВМ
факультета ВМК ННГУ.
sergey.bastrakov@gmail.com
Донченко Роман Владимирович,
лаборант НИЛ кафедры Математического обеспечения ЭВМ
факультета ВМК ННГУ.
ss.donchenko@itlab.unn.ru
Н.Новгород, 2012 г.
Параллельные численные методы.
93 из 83