Учитель математики МОУ «Гимназия № 4» Бродецкая Т. А, г.... применять изученные свойства для построения графиков чётной и Цель урока:

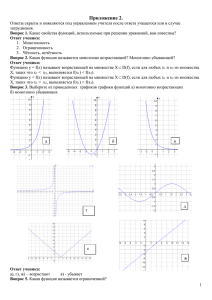
Учитель математики МОУ «Гимназия № 4» Бродецкая Т. А, г. Электросталь.
Тема урока: Чётные и нечётные функции.
Свойство графиков чётной и нечётной функции.
(9 класс, второй урок по теме).
Цель урока:
Рассмотреть свойство графиков чётной и нечётной функции и научиться
применять изученные свойства для построения графиков чётной и
нечётной функции.
Форма урока: лекция; практикум.
Методы:
наглядно – иллюстративный; медиа – лекция; проверочная работа.
Средства:
компьютер; обучающий диск «Уроки алгебры Кирилла и Мефодия. 9
класс». Виртуальная школа Кирилла и Мефодия [4]; интерактивная доска;
дидактический материал для проверки домашней работы (карточки);
дидактический материал для проведения проверочной работы (тест);
Используемые технологии:
- информационно – компьютерная технология с использованием электронного учебника;
- информационно – компьютерная технология с использованием интерактивной доски;
Ход урока: 1. Организационный момент.
2. Актуализация целей урока.
Цель нашего урока - рассмотреть свойство графиков чётной и нечётной функций и
научиться применять изученные свойства при построении графиков.
В конце урока - небольшая проверочная работа по теме «Чётные и нечётные функции».
3. Проверка домашнего задания и повторение вопросов теории.
1) 1 ученик – сформулировать определение чётной и нечётной функций. Записать на
доске необходимые равенства. (Готовится у доски).
2) 2 ученика решают задания по карточкам из домашней работы: № 486 (б) и № 484 (г)
(готовят на доске для проверки).
Устная работа.
1. Дайте определения следующим понятиям: а) Функция.
б) Область определения функции. Найти область определения
данных функций. Будет ли она симметрична относительно нуля?
у = х 3,
у = 8/х,
у = √х.
Что означает высказывание «область определения функции симметрична относительно
нуля»?
в) Область значений функции.
г) Нули функции.
д) Возрастание, убывание функции.
е) Чётность, нечётность (формулирует ученик, который
готовился у доски).
2. Является ли функция чётной, нечётной или ни чётной, ни нечётной?
а) у (х) = х5 ;
б) р (х) = х12 ;
в) f (х) = 3 х + 1,
г) у = √х.
3. Может ли быть чётной или нечётной функция, областью определения которой является:
а) промежуток
[ - 2; 5 ] ;
б) промежуток
( - 7; 7 );
в) объединение промежутков
[ - 10; - 2 ] U [ 2; 10 ] .
4. а) Функция f – чётная, f (3) = 25. Найти f (- 3).
б) Функция f – нечётная, f (- 8) = 71. Найти f (8).
1
4. Изучение нового материала.
Особое место среди функций занимают чётные и нечётные функции. Их графики удобно
строить, зная свойство их графиков.
Работа с учебником [1]. С помощью рис. 52 учебника из п.21 учитель вместе с классом
выясняет свойство графика чётной функции и формулирует его.
Доказательство данного свойства рассматривается с помощью медиа - лекции. ([4] Диск
«Виртуальная школа Кирилла и Мефодия. «Уроки алгебры Кирилла и Мефодия. 9
класс». Урок 13 «Чётные и нечётные функции»)
Обращается внимание учащихся
на то, как практически строить симметричный
относительно оси ординат график.
Работа устно:
На
одном из следующих чертежей <Рисунок 1> изображён график чётной функции.
Укажите этот чертёж. (Слайд на интерактивной доске).
<Рисунок 1>
Далее рассматривается свойство графика нечётной функции.
Работа с учебником [1]. С помощью рис. 53 учебника из п.21 учитель вместе с
классом выясняет свойство графика нечётной функции и формулирует его.
Работа устно:
На одном из следующих чертежей <Рисунок 2> изображён график нечётной функции.
Укажите этот чертёж. (Слайд на интерактивной доске).
<Рисунок 2>
2
Обращается внимание учащихся, что с примерами чётных и нечётных функций они уже
встречались в курсе алгебры. Одно из домашних заданий на следующий урок будет:
вспомнить изученные функции, какие из них являются чётными, какие – нечётными.
5. Закрепление изученного. Работа с учебником и интерактивной доской.
№ 487. Учащиеся выполняют самостоятельно в тетрадях, учитель фронтально проверяет.
Затем 2 учащихся выполняют на интерактивной доске задание для проверки, используя
маркеры разных цветов. При проверке учесть: D(f) = [ -3; 3].
№ 644 (а). Обсуждение подходов к выполнению задания:
1) построить график для х ≥ 0. Графиком будет являться луч с началом в точке с
абсциссой х = 0.
2) достроить график симметрично оси ординат. Начало луча – точка (0;-1) будет
симметрична сама себе. Точка (х;у) будет
симметрична точке (-х;у).
6. Проверочная работа (тест). (8 минут).
Работа на карточках. Пояснения к работе:
Часть заданий в виде теста. В заданиях 1, 2 необходимо выбрать график функции,
удовлетворяющий определённому условию.
Необходимо обвести номер графика и
поставить крестик в нужной клеточке таблицы после заданий. Будьте внимательны! В
заданиях 1 и 2 только один правильный ответ!
В 3 задании необходимо определить вид функции, пользуясь определением чётной и
нечётной функции. В 4 задании – достроить график функции, которая является либо чётной,
либо нечётной.
Во время выполнения проверочной работы учащимися учитель фронтально проверяет
домашнюю работу.
После сдачи карточек проверка работы с помощью интерактивной доски. (Слайды
заготовлены заранее).
Оценки за работу сообщаются учащимся на следующем уроке.
Текст проверочной работы приведён после пункта «Задание на дом».
7. Подведение итогов урока.
Повторение изученных свойств, выставление оценок.
8. Задание на дом.
п. 21, № 489, 644 (б), 645 (б). Дополнительное задание: выписать
известные чётные и нечётные функции, построить их графики.
3
Проверочная работа. 1 вариант.
На рисунке 3 укажите график чётной функции.
<Рисунок 3>
1.
2.
На рисунке 4 укажите график нечётной функции?
<Рисунок 4>
3. Определить, является ли функция чётной или нечётной.
а) f (x) = x8 – 3 x4. Решение:_____________________________________________________
______________________________________________________________________________
______________________________________________________________________________
б) f (x) = 12/х.
Решение:______________________________________________________
______________________________________________________________________________
______________________________________________________________________________
4. Достроить график функции f (x) на промежутке (- ∞; 0), зная, что f (x) – нечётная
функция и на промежутке [0 ; +∞) её график имеет вид, изображённой на рисунке 5:
<Рисунок 5>
Таблица ответов для заданий №1 и №2. Поставь крестик в клетке, содержащей верный
ответ. Будьте внимательны! В заданиях только один правильный ответ!
Варианты
ответа
1)
2)
3)
4)
Задание №1
Задание №2
Фамилия _______________________________________________________________________
4
Проверочная работа. 2 вариант.
На рисунке 6 укажите график чётной функции?
<Рисунок 6>
1.
2.
На рисунке 7 укажите график нечётной функции?
<Рисунок 7>
3. Определить, является ли функция чётной или нечётной.
а) f (x) = x7 – 2 x3. Решение:_____________________________________________________
______________________________________________________________________________
______________________________________________________________________________
б) f (x) = 6 /х.
Решение:______________________________________________________
______________________________________________________________________________
______________________________________________________________________________
4. Достроить график функции f (x) на промежутке (- ∞; 0), зная, что f (x) – чётная
функция и на промежутке [0 ; +∞) её график имеет вид, изображённый на рисунке 5:
<Рисунок 5>
Таблица ответов для заданий №1 и №2. Поставьте крестик в клетке, содержащей верный
ответ. Будьте внимательны! В заданиях только один правильный ответ!
Варианты
ответа
1)
2)
3)
4)
Задание №1
Задание №2
Фамилия _______________________________________________________________________
5
Используемый учебно-методический комплект:
1. Алгебра. Учебник для 9 класса общеобразовательных учреждений. Под редакцией С. А.
Теляковского. Москва. «Просвещение» 2004 г.
2. Дидактические материалы по алгебре. 9 класс. Ю. Н. Макарычев, Н. Г. Миндюк, Л. М.
Короткова. Москва. «Просвещение» 2005 г.
3. ФИПИ. ЕГЭ 2007 – 2008. Математика. «Реальные варианты».
4. Диск «Виртуальная школа Кирилла и Мефодия». «Уроки алгебры Кирилла и Мефодия.
9 класс».
6