Лекция №3-4 Динамика частицы Закон сохранения импульса 22/02/2014

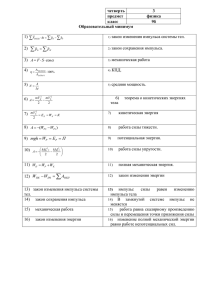
Лекция №3-4
Динамика частицы
Закон сохранения импульса
Алексей Викторович
Гуденко
22/02/2014
План лекции






Инерциальные системы отсчёта (ИСО)
Законы Ньютона.
Вес тела, невесомость.
Закон сохранения импульса. Импульс
силы
Теорема о движении центра масс.
Движение тел с переменной массой.
Реактивное движение. Формула
Циолковского.
Демонстрации 1




Воздушная дорога – свободные тела.
Массы тел.
Наклонная плотность с магнитным
(вязким) торможением
Наклонная плоскость с сухим трением,
критический угол.
Диамагнитная левитация –
невесомость???
Демонстрации 2





Воздушная дорога. Теорема о движении
центра масс. Закон сохранения импульса.
Стакан с водой на листе бумаги
Гиря на нитке
Сосновая планка на бумажных кольцах
Эфирная пушка
Динамика




Динамика – это раздел механики, изучающий законы
взаимодействия тел.
Сила – мера интенсивности взаимодействия тел,
проявляющаяся в изменении их количества движения.
В основе классической динамики лежат три закона
Ньютона.
1. Закон инерции, определение инерциальной системы
отсчёта (ИСО).
2. Уравнение движения материальной точки: в ИСО
a = F/m
3. Сила действия равна силе противодействия
F12 = - F21
Ньютоновская, или классическая нерелятивистская механика – это механика
малых (по сравнению со скоростью света) скоростей и больших (по сравнению с
массами атомов) масс.
Инерциальная система отсчёта (ИСО)


ИСО – система отсчёта, связанная со свободным телом.
Свободное тело – это тело, настолько удалённое от всех
других тел, что не подвержено действию внешних сил.

Как отличить ИСО от неИСО?
ключевой эксперимент: в ИСО свободное тело движется с
постоянной скоростью (по инерции).

Инерциальных СО - сколько угодно. Все они движутся
относительно друг друга равномерно-поступательно.

Чем хороши ИСО? В ИСО явления природы выглядят
наиболее просто.
Принцип относительности Галилея

Принцип относительности: механические явления
протекают одинаково во всех инерциальных СО  законы
механики одинаковы во всех ИСО
 Все ИСО по своим механическим свойствам эквивалентны.
Не существует выделенной ИСО.


Уравнения динамики инвариантны
по отношению к преобразованию
координат Галилея
Преобразование Галилея (K′ движется вдоль оси OX):
x = x′ + v0t; y = y′; z = z′; t = t′
Галилео Галилей (1564 –1642)
итальянский физик, механик и
астроном.
Принцип относительности: «Дайте движение кораблю, и притом с какой
угодно скоростью; тогда (если только движение его будет равномерным, а не
колеблющимся туда и сюда) вы не заметите ни малейшей разницы»
Закон инерции: «…если бы все сопротивления были уничтожены, то его (тела)
движение было бы вечно равномерным, если бы плоскость простиралась в
бесконечность» («неистребимо запечатлённое движение»).
В 1992 папа Иоанн Павел II объявил решение суда
инквизиции ошибочным и реабилитировал Галилея.
Примеры инерциальных систем
отсчёта


Геоцентрическая СО – система связанная с Землёй –
приблизительно инерциальная СО: инерциальность
«портит» ускорение, возникающее из-за с суточного
вращения:
1.
a = ω2R = 0,34 м/с2 1 кг на экваторе «легче», чем 1 кг
на полюсе на 0,34 г.
2.
При падении с высоты 100 м камень отклоняется к
востоку на ~ 1 см (на экваторе).
3.
Маятник Фуко: в наших широтах плоскость качаний
поворачивается на ~ 100 за час.
4.
Звёзды (свободные тела) вращаются по окружностям,
а значит с центростремительным ускорением 
Гелиоцентрическая СО (система Коперника): начало – в
центре Солнца, оси – на далёкие звёзды.
Маятник Фуко (1851 г.)

Задача Капицы:
Астрономические наблюдения показывают, что на
планете Венера полная облачность, так что
«жители» Венеры лишены возможности
наблюдать небесные светила. Опишите, каким
методом они могли бы точно измерить длину своих
суток.

маятник Фуко Московского планетария:
длина нити 16 метров,
массой шара — 50 килограммов
Первый закон Ньютона – закон
инерции = def ИСО

Системы отсчёта (СО), в которых свободное
тело движется равномерно, называются
инерциальными СО системы называются
инерциальными.
Второй закон Ньютона

В инерциальной системе отсчёта скорость
изменения импульса тела равна действующей
на тело силе:
dp/dt = F 
mdv/dt = F 
ma = F 
md2r/dt2 = F – уравнение движения

Состояние материальной точки однозначно
определяется начальными условиями и
уравнением движения.
Третий закон Ньютона


Силы, с которыми две материальные
точки действуют друг на друга, всегда
равны по величине и направлены в
противоположные стороны вдоль прямой,
соединяющий эти точки: F12 = - F21
Силы взаимодействия всегда возникают
парами; обе силы приложены к разным
точкам (телам) и являются силами одной
природы.
Фундаментальные взаимодействия
Фундаментальные взаимодействия:
1) гравитационное;
2) электромагнитное;
3) сильное или ядерное (обеспечивающее связь
частиц в ядре);
4) слабое (ответственное за многие процессы
распада элементарных частиц)
Силы в механике
1.
2.
3.
4.
5.
Однородная сила тяжести (гравитационная природа):
F = mg, g = GM/R2 = 9,8 Н/кг = 9,8 м/с2 – ускорение
свободного падения вблизи поверхности Земли.
Упругая сила, пропорциональная величине деформации x
(закон Гука):
Fупр = - kx = - k(l – l0), k – коэффициент жёсткости.
Сила трения скольжения:
F = μN, μ – коэффициент трения, зависящий от природы
соприкасающихся поверхностей. F направлена вдоль
соприкасающихся поверхностей против скорости.
Силы вязкого трения:
F = - kv, k – определяется геометрическими размерами
тела и вязкостью среды
Сила лобового сопротивления F = βSv2
Применение законов динамики





Вес тела в лифте. Невесомость. Перегрузка.
Автомобиль на выпуклом (вогнутом) мосту. «Мёртвая
петля». Спутник на орбите.
Наклонная плоскость с трением. Критический угол.
Трение покоя, или как удержать тонну.
Верёвка, навитая на столб, или как удержать 1 т груза
(2.56): μ = 1/π; T = 10000 H.
Наклонная плоскость с магнитным (вязким)
торможением.
Вес тела. Невесомость. Перегрузка.








Вес тела – это сила, с которой тело вследствие
притяжения к Земле действует на неподвижную
относительно тела опору или подвес.
На рисунке - вес тела P = - N
Ускорение вверх: mg + N = ma  - mg + N = ma 
N = m(g + a)  P = N = m(g + a)
Ускорение вниз: mg + N = ma  - mg + N = - ma 
N = m(g - a)  P = N = m(g – a)
P = m(g – a)
Перегрузка: k = P/mg
Невесомость возникает, если тело движется под
действием только силы тяжести: a = g  P = 0
Искусственная невесомость:
свободное падение, полёт по баллистической
траектории, магнитная левитация
Y
g
a
N
mg
0
P
Лауреаты Нобелевской премии по физике
2010 года – выпускники Физтеха

Нидерландский физик Андрей Гейм (МФТИ, ФОПФ, 1982 г.) и
британский физик Костя Новосёлов (МФТИ, ФФКЭ, 1997 г.)
Нобелевская премия присуждена за открытие и исследование графена –
мономолекулярного слоя графита с уникальными электронными,
механическими и оптическими свойствами
Магнитная микрогравитация.
Фотографии из статьи:
Geim A. Everyone`s Magnetism, Physics Today, September 1998.
Магнитная левитация живого организма.
Андрей Гейм.
Шнобелевская  премия (2000 г.)

Фотография из статьи:
Geim A. Everyone`s
Magnetism, Physics
Today, September 1998.
Левитирующая в
магнитном поле лягушка
Левитация карандашного грифеля

Грифель диаметром d = 0,5 мм из
автоматического карандаша левитирует над
сильным постоянным магнитом
Импульс частицы p = mv
Изменение импульса = импульсу силы:
dP = Fdt

P = mv – импульс частицы
dp = Fdt  Δp = ∫Fdt - приращение импульса частицы равно
импульсу силы
Импульс, приобретаемый телом, определяется силой и
временем её действия ΔP = ∫Fdt = Fср Δt
Демонстрации
 Стакан с водой на листе бумаги
 Гиря на нитке
 Сосновая планка на бумажных кольцах
Импульс системы частиц P = Σpi



импульс системы частиц P = Σpi
dP/dt = Σdpi/dt = ΣFiвнутр + ΣFiвнешн = ΣFiвнешн = Fвнешн
Производная импульса системы частиц по времени
равна векторной сумме всех внешних сил,
действующих на частицы системы.
Изменение импульса системы равна импульсу
результирующей всех внешних сил:
ΔP = ∫ Fвнешнdt
Закон сохранения импульса


Замкнутая или изолированная система
тел – система тел, взаимодействующих
только друг с другом, и не
взаимодействующих с другими телами.
Импульс замкнутой системы тел остаётся
постоянным при любых взаимодействиях
тел этой системы между собой.
Закон сохранения импульса:
опыт на воздушной дороге


Ключевой опыт: при столкновении двух тел
|Δv1|/|Δv2| = m2/m1 – не зависит способа
взаимодействия и интенсивности
взаимодействия m1 Δv1 = - m2 Δv2  m1v1 + m2v2 =
m1v′1 + m2v′2
Закон сохранения импульса: полный импульс
замкнутой системы двух взаимодействующих
частиц сохраняется:
P = P1 + P2 = const
Центр масс системы. Терема о
движении центра масс



Центра масс:
rc = (m1r1 + m2r2 + …+mnrn)/(m1 + m2 + …+mn) rc = Σmiri/m;
m = Σmi – масса системы
Скорость Центра масс:
vc = Σmivi/m = P/m
Импульс системы: P = Σmivi = mvc – импульс системы
равен произведению массы системы на скорость её
центра масс 
mdvc/dt = Fвнешн

Теорема о движении Центра масс:
Центр масс системы движется как материальная точка,
масса которой равна суммарной массе всей системы, а
действующая сила – сумме внешних сил
Центр масс замкнутой системы



Центр масс замкнутой системы частиц
движется равномерно и прямолинейно.
Инерциальная СО, связанная с центром
масс замкнутой системы называется
системой центра инерции, или
С-системой.
В С-системе полный импульс системы
равен нулю
Теорема о движении центра масс.
Примеры и демонстрации

Воздушная дорога (демонстрация):
1.
2.



взаимодействие тележки с двойной тележкой,
соединённой пружинкой.
Колебания двойной тележки.
Центр масс разорвавшегося на множество
осколков снаряда продолжает двигаться по
параболической траектории.
Муха в пробирке.
Задача о рыбаке и лодке.
Муха в пробирке (№ 3.4)




Массы мухи и пробирки одинаковы
M=m
Длина пробирки L
Время падения пробирки t = ?
Решение:
(M + m)dVc/dt = (M + m)g 
dVc/dt = g 
Vc = gt 
S = ½L = gt2/2 
t = (L/g)1/2
g
C1
L/2
C2
Движение тел с переменной массой.
Реактивное движение



Закон сохранения (изменения) импульса:
(m + dm)(v + dv) + vгазdmгаз - mv = Fdt
dmгаз = -dm; vгаз = v + u 
mdv/dt = u dm/dt + F = -μu + F
основное уравнение динамики точки с
переменной массой или уравнение
Мещерского.
Fр = -μu – реактивная сила
Формула Циолковского



F = 0  mdv/dt = - u dm/dt 
v = uln(m0/m), или m0/m = ev/u – формула
Циолковского
В поле тяжести: v = uln(m0/m) – gt
dv/dt = 0 (ракета зависла):
Fр = mg  m = m0e-gt/u  μ = (m0g/u) e-gt/u
Константин Эдуардович Циолковский (1857 – 1935) –
основоположник современной космонавтики
Константин Эдуардович
Циолковский - русский и советский
учёный-самоучка, исследователь,
школьный учитель. Основоположник
современной космонавтики.
Обосновал
вывод уравнения реактивного
движения, пришёл к выводу о
необходимости использования
«ракетных поездов» — прототипов
многоступенчатых ракет.
Автор работ по аэродинамике,
воздухоплаванию и другим наукам.
Расчёт запаса топлива для разгона до
первой (второй) космической скорости




VI = (gR)1/2 = 7,9 км/с
VII = (2gR)1/2 = 11,2
км/с
U ~ 2 км/с – скорость
истечения газов
VI: m0/m = ev/u ~ 52 
m/m0 ~ 2%
VII: m0/m = ev/u ~ 270
 m/m0 ~ 0,4%