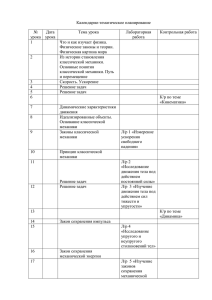
4. виды, содержание и объемы разделов дисциплины

2
1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ
Цель дисциплины состоит в изучении одного из основных разделов теоретической физики и формировании у студентов навыков научного мышления.
Задачи дисциплины – дать знания по вопросам:
 Место классической механики в современной физике и область ее применимости;
 Математические методы описания движения материальных точек;
 Вариационные принципы механики;
 Фундаментальные методы механики – Ньютона, Лагранжа, Гамильтона, ГамильтонаЯкоби;
2. МЕСТО ДИСЦИПЛИНЫ В СТРУКТУРЕ ООП
2.1. Междисциплинарные связи с обеспечивающими (предыдущими) дисциплинами
Для успешного освоения дисциплины необходимы знания, полученные из курсов математического анализа и дифференциальных уравнений. Желательно также знания механики
в объеме общего курса физики.
2.2. Междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
Курс теоретической механики играет важнейшую роль в подготовке специалистов физических специальностей. Знания, полученные из курса, необходимы для успешного освоения целого ряда дисциплин учебного плана, в частности, квантовой механики, статистической физики,
физики твердого тела и др.
3. ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОСВОЕНИЯ ДИСЦИПЛИНЫ
В результате освоения дисциплины студент должен:
Знать:
 основные понятия классической механики;
 уравнения, описывающие движение систем материальных точек;
 вариационные принципы классической механики;
 основные приближенные подходы, используемые в электродинамике;
Уметь:
 определять число степеней свободы механической системы;
 вводить обобщенные координаты;
 составлять функции Лагранжа и Гамильтона и получать из них уравнения движения;
 находить интегралы движения;
 определять частоты малых колебаний механической системы около положения
равновесия;
Владеть:
 навыком составления уравнений движения для обобщенных координат и импульсов;
 навыком решения задач механики и использования для этой цели требуемых математических приемов и методов;
 простейшими приемами решения обыкновенных дифференциальных уравнений
второго порядка, возникающими в задачах механики.
3
4. ВИДЫ, СОДЕРЖАНИЕ И ОБЪЕМЫ РАЗДЕЛОВ ДИСЦИПЛИНЫ
4.1
Содержание разделов дисциплины
4.1.1. Механика Ньютона.
Основные понятия классической механики. Инерциальные системы отсчета. Принцип
относительности Галилея. Законы Ньютона и силы взаимодействия между материальными
точками. Методы составления и решения уравнений Ньютона в криволинейных координатах.
4.1.2 Метод Лагранжа.
Задача динамики несвободной системы и понятие о связях. Типы связей. ПринципД’Аламбера. Уравнения Лагранжа первого рода. Обобщенные координаты, скорости и
силы. Уравнения Лагранжа второго рода. Диссипативная функция Рэлея. Общие свойства
функции Лагранжа. Примеры составления лагранжианов и уравнений движения.
4.1.3 Метод Гамильтона.
Функция Гамильтона и канонические уравнения. Связь лагранжиана и функции Гамильтона. Уравнения Рауса. Скобки Пуассона и их свойства. Канонические преобразования.
Фазовое пространство и теорема Лиувилля.
4.1.4 Интегралы движения.
Циклические переменные и интегралы движения. Общие условия сохранения физической величины в механике. Закон сохранения энергии. Закон сохранения импульса. Закон
сохранения момента импульса (углового момента). Преобразования сохраняющихся величин. Центр инерции.
4.1.5 Метод Гамильтона-Якоби.
Действие как функция времени и координат механической системы. Уравнение Гамильтона-Якоби. Его решение методом разделения переменных. Укороченное действие.
4.1.6 Вариационные принципы механики.
Основные понятия вариационного исчисления. Функционал действия. Принцип Гамильтона. Уравнения Лагранжа как уравнения экстремалей для функционала действия. Вывод канонических уравнений из принципа наименьшего действия. Роль принципа наименьшего действия в физике.
4.1.7 Задачи классической механики.
Анализ одномерного движения в поле потенциальной силы. Задача двух взаимодействующих тел. Движение частицы в центральном поле. Движение в гравитационном (или кулоновском) поле. Законы Кеплера.
4.1.8 Малые колебания.
Свободные одномерные колебания. Свободные колебания системы с несколькими
степенями свободы. Вынужденные одномерные колебания. Вынужденные колебания при
наличии трения.
4.1.9Движение твердого тела.
Угловая скорость. Тензор инерции. Момент импульса и уравнения движения твердого
тела. Углы Эйлера. Динамические уравнения Эйлера. Движение волчка.
4
Разделы дисциплины и виды занятий
Перечень разделов дисциплины с указанием трудоемкости их освоения в часах, видов учебной работы и промежуточной аттестации с учетом существующих форм освоения
приведен в табл. 4.2.1., 4.2.2.
4.2
Таблица 4.2.1.
Распределение аудиторной нагрузки и контрольных мероприятий
для изучаемой дисциплины по разделам
4.1.1
4.1.2
4.1.3
4.1.4
4.1.5
4.1.6
4.1.7
4.1.8
4.1.9
Механика Ньютона.
Метод Лагранжа.
Метод Гамильтона.
Интегралы движения.
Метод ГамильтонаЯкоби.
Вариационные
принципы механики.
Задачи классической
механики.
Малые колебания.
Движение твердого
тела.
4
8
8
4
11
8
3
4
8
6
2
4
6
4
2
4
6
4
2
4
4
4
4
10
8
2
4
9
5
4
4
6
4
2
Всего:
68
51
17
0
0
0
0
0
0
0
0
Домашние работы
Контрольные работы
Коллоквиумы
Рефераты
Расчетные работы
Графические работы
Расчетнографические работы
Курсовые работы
Курсовые проекты
Лабораторные
работы (ЛР)
Практические
занятия (ПЗ)
Лекции (Л)
Наименование раздела
Всего часов
Семестр изучения
Номер раздела
Раздел дисциплины
Общая трудоемкость дисциплины по учебному плану (час.): 102
Аудиторная
Число контрольных мероприятий
нагрузка (час.)
0
Всего
4
Экзамен
Лаборат.
Работы
Зачет
Аудиторная нагрузка
(час.)
Практич.
Занятия
Промежут.
аттест.
Лекции
Семестр
изучения
Таблица 4.2.2.
Распределение аудиторной нагрузки и объема самостоятельной работы
по семестрам изучения дисциплины
Объем
СРС
(час.)
+
51
17
0
68
34,0
9,3
0
0
0
0
0,0
0,0
0
0
0
0
0,0
0,0
51
17
0
68
34,0
9,3
Всего:
Резерв
на СРС
(час.)
5. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ И САМОСТОЯТЕЛЬНАЯ РАБОТА
5.1.
Лабораторный практикум
не предусмотрен
5
0
5.2.
Практические занятия
Примерные темы практических занятий с указанием разделов дисциплины, к которым
они относятся, приведены в табл. 5.2.
Таблица 5.2
Распределение практических занятий по разделам изучаемой дисциплины
Номер Номер
раздела занятия
5.3.
4.1.2
1-2
4.1.3
4.1.4
4.1.5
4.1.7
3
4
5
6
4.1.8
7
4.1.8
4.1.8
8
9
Тема занятия
Конструирование лагранжианов и составление
уравнений движения
Канонические уравнения
Нахождение сохраняющихся величин
Интегрирование уравнений Гамильтона-Якоби
Одномерное движение
Нормальные координаты и частоты малых колебаний
Вынужденные колебания и резонанс
Колебания физического маятника
Всего:
Время на
проведение
занятия (час.)
3
2
2
2
2
2
2
2
17
Перечень тем рефератов
не предусмотрен
5.4
Перечень тем домашних работ
не предусмотрен
5.5
Перечень тем контрольных работ
не предусмотрен
5.6
Перечень тем расчетных работ
не предусмотрен
5.7
Перечень тем расчетно-графических работ
не предусмотрен
5.8
Тематика коллоквиумов
не предусмотрен
6. ТЕМАТИКА КУРСОВОГО ПРОЕКТИРОВАНИЯ
не предусмотрено
7. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
7.1
Рекомендуемая литература
7.1.1 Основная литература
1. Ольховский И. И. Курс теоретической механики для физиков. – М.: Лань, 2009.
6
2. Барановский В.Н., Левина Г.А. Теоретическаямеханика. Учебноепособие – М.: Лань,
2008.
3. Н.Н. Бухгольц. Основной курс теоретической механики, ч.1,2. М.: Лань, 2009.
4. Н.Н. Никитин. Курс теоретическоймеханики. – М.: Лань, 2010.
5. Журавлев В.Ф. Основы теоретической механики. – М.:Физматлит, 2010.
6. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика.т. I. Механика– М.:Физматлит,
2004.
7.1.2 Дополнительная литература
1. М.А. Айзерман. Классическая механика. М.:Физматлит, 2005
2. Андронов А.А., Витт С.Э., Хайкин Теория колебаний. 3-е изд. – М. Наука, 1981.
3. Арнольд В.И. Математические методы классической механики. – М. Наука,1974.
4. Коткин Г.Л. Сербо В.Г. Сборник задач по классической механике. – М. Наука, 1969.
5. Парс Л.А. Аналитическая механика. – М. Наука, 1971.
7.1.3 Методические разработки кафедры
1. А.Б. Борисов, Л.Г. Скорняков. Методическое пособие «Ньютонова механика», УГТУУПИ, 2008
2. А.Б. Борисов, Л.Г. Скорняков. Методическое пособие «Лагранжева механика», УГТУУПИ, 2008
3. Л.Н. Новиков. Методическое пособие «Колебания и волны», УГТУ-УПИ, 2006
Программное обеспечение
7.2
не требуется
Базы данных, информационно-справочные и поисковые системы
7.3
http://study.ustu.ru
8. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Общие требования
8.1
Лекционный материал может изучаться в обычной аудитории, оборудованной доской
для записей. Также может быть полезным наличие проектора, соединенного с персональным
компьютером для демонстрирования электронной версии курса на настенном экране.
8.2
Сведения об оснащенности дисциплины специализированным и лабораторным
оборудованием
специализированное оборудование не требуется
9. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
Рекомендации для преподавателя
9.1



глубокое освоение теоретических аспектов тематики курса, ознакомление, переработку литературных источников; составление списка литературы, обязательной для изучения и дополнительной литературы; проведение собственных исследований в этой
области;
разработку методики изложения курса: структуры и последовательности изложения
материала; составление тестовых заданий, контрольных вопросов;
разработку методики проведения и совершенствование тематики практических занятий;
7


Рекомендации для студента
9.2


9.3
разработка методики самостоятельной работы студентов;
постоянную корректировку структуры, содержания курса.
посещение лекций ведущего преподавателя; лекции – основное методическое руководство при изучении дисциплины, оптимальным образом структурированное и скорректированное на современный материал; в лекции глубоко и подробно, аргументировано и методологически строго рассматриваются главные проблемы темы; в лекции
даются необходимые разные подходы к исследуемым проблемам;
обязательная работа с рекомендованной литературой; без самостоятельной работы
невозможно успешное усвоение новых знаний.
Перечень контрольных вопросов для подготовки к текущей аттестации по дисциплине
Какие переменные задают фазовое пространство в гамильтоновой формулировке механики?
Какие переменные задают конфигурационное пространство в лагранжевой формулировке
механики?
Сколько степеней свободы имеет система, состоящая из N частиц, в которой две частицы
соединены жестким стержнем?
Сколько степеней свободы имеет система N частиц, на которую не наложены связи?
Сколько постоянных интегрирования содержится в решении уравнений движения, описывающих динамику системы из N частиц без связей?
Чему равно число независимых интегралов движения в замкнутой механической системе
из N частиц без связей?
Как формулируется принцип Гамильтона?
Какие симметрии пространства и времени классической механики приводят к выполнению
закона сохранения импульса?
Какие симметрии пространства и времени классической механики приводят к выполнению
закона сохранения энергии?
Какие симметрии пространства и времени классической механики приводят к выполнению
закона сохранения момента импульса?
Принцип экстремального действия можно представить так:
Уравнения Лагранжа для системы частиц в случае действия потенциальных сил имеют
вид:
Уравнения Лагранжа для системы частиц при наличии диссипативных сил имеют вид:
Уравнения Лагранжа для системы невзаимодействующих частиц имеют вид:
Какие динамические характеристики частиц задают состояние механической системы в
лагранжевой формулировке механики?
Что необходимо задать для определения сохраняющихся величин в механических системах?
Уравнения Гамильтона имеют вид:
Какие преобразования называются каноническими?
Функция Гамильтона одномерного гармонического осциллятора имеет вид:
Функция Гамильтона пространственного гармонического осциллятора имеет вид:
Функция Гамильтона однородного поля тяжести имеет вид:
8
9.4
Перечень ключевых слов дисциплины
Таблица 9.4.
Ключевые слова
Номер
раздела
Наименование
раздела
4.1.1
Механика Ньютона.
4.1.2
Метод Лагранжа.
4.1.3
Метод Гамильтона.
4.1.4
Интегралы движения.
Метод ГамильтонаЯкоби.
Вариационные принципы механики.
Задачи классической
механики.
4.1.5
4.1.6
4.1.7
4.1.8
4.1.9
Малые колебания.
Движение твердого
тела.
Ключевые слова раздела
Инерциальные системы отсчета; уравнения
Ньютона
Связи; обобщенные координаты; функция
Лагранжа
Функция Гамильтона; канонические уравнения; скобки Пуассона
Циклические переменные
Канонические преобразования; производящая
функция; действие
Принцип наименьшего действия
Разделение переменных; одномерное движение; задача Кеплера
Условия равновесия; нормальные координаты
Углы Эйлера; тензор инерции; симметричный волчок
10. ЛИСТ РЕГИСТРАЦИИ ИЗМЕНЕНИЙ
Номер
изменения
Номер пункта
ИзмеНового
ненного
Изъятого
Дата
Подпись ответственВсего листов
внесения
ного за внесение
в документе
изменения
изменений
9
Содержание
1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ
2. МЕСТО ДИСЦИПЛИНЫ В СТРУКТУРЕ ООП
3. ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОСВОЕНИЯ
ДИСЦИПЛИНЫ
4. ВИДЫ, СОДЕРЖАНИЕ И ОБЪЕМЫ РАЗДЕЛОВ
ДИСЦИПЛИНЫ
5. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ И
САМОСТОЯТЕЛЬНАЯ РАБОТА
6. ТЕМАТИКА КУРСОВОГО ПРОЕКТИРОВАНИЯ
7. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
8. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ
ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
9. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО
ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
10. ЛИСТ РЕГИСТРАЦИИ ИЗМЕНЕНИЙ
10
3
3
3
4
5
6
6
7
7
9