Пермский государственный технический университет
реклама

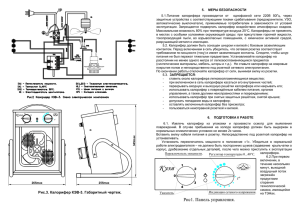
Пермский государственный технический университет. Кафедра теплотехники. Курсовая работа по теме: Теплообменные аппараты Выполнил: студент гр. ТВз-05 Пуговкин А В Проверил: Лошманов Игорь Петрович 2008 Содержание: Вспомогательные расчеты, выбор типа калорифера. Средний логарифмический температурный напор. Теплофизические свойства теплоносителей. Коэффициент оребрения. Определение коэффициентов теплоотдачи. Определение коэффициентов теплопередачи. Вычисление поверхности нагрева, компоновка теплообменного аппарата (ТОА). 8. Проверочный расчет ТОА. 9. График температурного поля ТОА. 10. Список литературы 1. 2. 3. 4. 5. 6. 7. 4 5 6 6 7 9 9 9 11 12 1. Вспомогательные расчеты, выбор типа калорифера. По характеристикам калориферов (задание на курсовую работу) предварительно выберем калориферы: КФМ – 4…6; КФС – 4…11; КФБ – 4…11. 3 Определяем площадь проходного сечения обеспечивающую проход воздуха со скоростью 2 18,079 м с (задание на курсовую работу). f2 G2 , м2 2 G2 11921 кг ч . – расход воздуха; – плотность воздуха, кг м 3 . – вычисляем по средней температуре из методички. Среднюю температуру воздуха определим как среднеарифметическое его температур на вводе и на выходе: t 2' t 2'' 13 27 t2 20 C 2 2 3 1,205 кг м . 11921 f2 0,152 м 2 3600 18,079 1,205 По данному проходному сечению выбираем калориферы: КФМ – 3; КФС – 3; КФБ – 3. Рекомендации: Калорифер малой серии КФМ рекомендуется брать с расходом воздуха до 10000 кг ч , калорифер средней серии КФС – 10000 - 20000 кг ч , калорифер большей серии КФБ – 20000 - 40000 кг ч . Учитывая, что по механическим потерям, расход воздуха может иметь пятикратный запас, для расхода менее 10000 кг ч выбираем калориферы серии КФМ, более 10000 кг ч – КФС. По данным рекомендациям выбираем калорифер КФС – 3. По рекомендации преподавателя выбираем калорифер КФМ – 3 проходным сечением по воздуху 0,154 м 2 . Уточняем скорость воздуха через калорифер с выбранным проходным сечением 0,154 м 2 . G2 11921 17,844 м с f 0.154 1.205 3600 18,079 17,844 100 1,3% – погрешность в пределах нормы. 18,079 2 Определяем расход воды в калорифере. G1 1 f1 , кг ч . Принимая что средняя температура горячего теплоносителя равна 75-80 С , принимаем плотность воды 960 кг м 3 . 1 – скорость воды в калорифере (задание на курсовую работу). f1 – площадь всех трубок проходного сечения калорифера КФМ – 3. Определение площади сечения трубок КФМ-3 d вн2 3,14 0,018 2 f1 16 16 0,0041 м 2 . 4 4 G1 0.096 0.0041 960 3600 1360,282 кг ч . 4 '' Определяем температуру воды на выходе из калорифера t 1 . Температуру горячего теплоносителя определим из уравнения теплового баланса при условии отсутствия тепловых потерь и фазовых переходов Q1=Q2=Q Q1 W1 t1' t1'' , Вт. t1'' t1' Q , С W1 W1 c1 G1 , Вт / С При расчетах Q определяем по параметрам воздуха: 11921 27 13 0.24 41863600 46574,552 Вт Q c 2 G2 t 2'' t 2' Дж . кг град 46574,552 3600 t1'' 98 68,5 С . 4186 1360,282 своды= 4186 Среднюю температуру горячего теплоносителя определим как среднеарифметическое его температур на вводе и на выходе: t1 t1' t1'' 98 68,5 83,25 C . 2 2 2. Средний логарифмический температурный напор. Сначала определим среднелогарифмический температурный перепад как для чисто противоточных аппаратов: t пр t1' t 2' t1'' t 2'' t ' t '' (98 27) (68,5 13) 62,9 С ' ' ' 98 27 t t t ln ln '' ln 1'' 2'' 68,5 13 t t1 t 2 Далее вычисляем вспомогательные величины P и R: t 2'' t 2' 27 13 P ' ' 0,16 t1 t 2 98 13 t1' t1'' 98 68,5 R '' ' 2,1 27 13 t2 t2 По этим данным из вспомогательного графика (прил. I «Методические указания к курсовой работе»), находим поправку t . t f ( P, R) 0,98 Средний температурный напор для перекрестного тока t ср t пр t 62,9 0,98 61,64 С . 3. Теплофизические свойства теплоносителей. Теплофизические свойства теплоносителей определяются при их средних температурах методом интерполяции. 5 Теплофизические свойства воды. При t1 t1 t1 98 68,5 83,25 °С 2 2 t 80C; 0,675 Вт м2 ; 0,365 10 6 ; Pr 2,21; 6,32 10 4 К 1 мK с 2 Вт 6 м t 90C; 0,680 ; 0,326 10 ; Pr 1,95; 6,95 10 4 К 1 мK с Коэффициент теплопроводности: 1 (83,25) 0,675 0,675 0,68 Вт 3,25 0,677 10 мK Кинематическая вязкость: 2 0,365 0,326 6 6 м 1 (83,25) (0,365 3,25) 10 0,3523 10 10 с Число Прандтля: Pr1 (83,25) 2,21 2,21 1,95 3,25 2,13 10 Число Грасгофа: (83,25) 6,32 6,32 6,95 3,25) 10 4 6,52 10 4 10 Теплофизические свойства воздуха. t 2 t 2 13 27 20C 2 2 2 2 Вт 6 м t 2 20C; 2 2,59 10 ; 2 15,06 10 ; Pr 0,703 мK с При t 2 4. Коэффициент оребрения. Отношение F рс Fс F р Fn Fс F р с Fс называется коэффициентом оребрения. , где Fр - площадь ребер; Fn - площадь стенок трубок в промежутках между ребрами; Fс - площадь внутренней гладкой поверхности трубок. nтр d н Fр 2 l 2 l1 4 4 3,14 0,022 2 n р 2 0,084 0,116 180 2,96 м 2 , 4 где l 2 ,l1 - длина и ширина ребра; nтр - число труб в секции; d н - наружный диаметр трубок; 1 nр 1 180шт. - число ребер на 1 погонный метр трубы; 0,0055 0,0055м – шаг расположения ребер. 6 Fn d н d н n р nтр (3,14 0,022 3,14 0,022 0,0005 180) 4 0,251м 2 , где - толщина ребра. Fс d вн nтр 3,14 0,018 4 0,22608 м 2 , где d в н - внутренний диаметр трубок. Коэффициент оребрения F рс Fс 2,96 0,251 14,21 0,226 5. Определение коэффициентов теплоотдачи. 5.1 Найдем коэффициент теплоотдачи от воды к стенке 1 Nu1 1 19,74 0,677 Вт 742,44 2 d вн 0,018 м K 1 . При средней температуре воды t1 83,25С Выбранный по определяющей температуре стенки 20 83,25 51,63С 2 Prw (51,63) t 50C ; Pr 3,54 t 60C ; Pr 2,98 3,54 2,98 1,63 3,45 Prw (51,63) 3,54 10 tw Для выбора уравнения подобия теплоотдачи при движении жидкости внутри трубы необходимо найти число Рейнольдса: Re 1 W1 d вн 1 0,0,96 0,018 4904,91 0,3523 10 6 Поскольку 2 10 3 Re 10 4 , режим движения жидкости переходный. Для решения уравнения подобия находится значение комплекса К 0 комплекс, зависящий от числа Рейнольдса: К 0 f Re 4103 12,2 К 0 f Re 5103 16,5 К 0 f Re 4909,91 12,2 16,5 12,2 904,91 16,09 1000 Находим число Нуссельта: Nu1 К0 Pr Pr10, 43 1 Prw 0 , 25 16,09 2,13 0 , 43 2,13 3,45 0 , 25 19,74 5.2 Определяем коэффициент теплоотдачи от ребристой стенки к воздуху 2 . 7 2 Nu2 2 21,44 2,59 10 2 Вт 100,96 2 b 0,0055 м K Расчет числа Нуссельта в пучках с круглыми и квадратными ребрами, обтекаемыми поперечным потоком газа, произведем по формуле: Nu 2 0,096 Re 0, 72 2 d н b 0, 54 h b 0,14 , где b 0,0055 м - шаг ребер; d н 0,022 м - наружный диаметр трубы; h 0,018 м - высота ребра; Re 2 - число Рейнольдса b 17,844 0,0055 Re 2 (20) 2 6516,73 2 15,06 10 6 коэффициент теплопроводности 2 (20) 2,59 10 2 Вт , мK м2 , с при скорости движения воздуха 2 17,844 м с кинематическая вязкость 2 (20) 15,06 10 6 Nu2 0,096 6516,73 0, 72 0,022 0,0055 0, 54 0,018 0,0055 0,14 21,44 Определенный таким образом коэффициент теплоотдачи необходимо умножить на поправочный множитель, учитывающий неравномерность теплообмена по поверхности ребра: Fp 0 2 пр 2 Fn F pc , где F pc 1 Fр 4,44 м 2 - площадь ребристой поверхности, равная площади ребер; Fn 0,3774 м 2 - площадь стенок трубок в промежутках между ребрами; Fpc Fp Fn 4,44 0,3774 4,8174 м 2 ; 0 - разность между температурами поверхностей ребер и воздуха; 1 - разность между температурами основной поверхности трубы и воздуха. Отношение 0 0,6 следует принять одинаковым для всех типов 1 калориферов («Методические указания к курсовой работе»), тогда Fp 0 F n F pc 1 F pc 2,96 0,251 0,6 0,631 3,211 3 , 211 Поправочный множитель 0,631 получается одинаковым для всех типов калориферов. Приведенный коэффициент теплоотдачи 2 пр 100,96 0,631 63,71 Вт м2 K 8 6. Определение коэффициентов теплопередачи. Кр где 1 1 ст 1 ст F pc 1 Fc 2 пр 1 Вт 28,2 2 м K 0,002 3,211 1 1 742,44 45,4 0,226 63,71 0,022 0,018 0,002 м - толщина стенки трубок калорифера; 2 Вт 45,4 мK ст ст 7. Вычисление поверхности нагрева, компоновка теплообменного аппарата (ТОА). Расчетную поверхность нагрева определим из уравнения теплопередачи. Q К р Fп t ср Fп Q 46574 26,79 м 2 К р t ср 28,2 61,64 Площадь калорифера КФМ-3 – 8,5 м 2 . Следовательно, для реализации задания необходимо количество калориферов: m Fп 26,79 3,15 шт. S 8,5 Округлив это число до целого значения, получим, что калориферная установка должна состоять из 4 калориферов КФМ-3. Выводы: Калориферная установка состоит из 4 калориферов КФМ-3. Калорифер КФМ-3 состоит из 4 секций. Для приближения фактической площади нагрева к расчетной необходимо при монтаже калориферной установки отключить 3 секции. Поскольку площади проходных сечений по воде и по воздуху принимались в расчете для одного калорифера, то схема соединения и по воде, и по воздуху будет последовательной. Установленная поверхность нагрева калориферной установки оказалась больше расчетной, поэтому можно нагреть большее количество воздуха при тех же параметрах, либо нагреть воздух до более высокой температуры на выходе. 8. Проверочный расчет ТОА Аналитический расчет тепловых аппаратов с перекрестным током довольно сложен и базируется на работе, выполненной Нуссельтом в 1911 г. Для приближенных расчетов можно рекомендовать уравнения, в которых известными величинами являются поверхность аппарата F , коэффициент теплопередачи K , условные эквиваленты W1 и W2 и начальные температуры t1' и t 2' . Требуется найти конечные температуры t1'' , t 2'' и количество теплоты Q . Количество теплоты, отдаваемое горячим теплоносителем, составляет Q W1 t1' t1'' , 9 откуда конечная температура равна t1'' t1' Q , W1 Для холодного теплоносителя Q W2 t 2'' t 2' , откуда t 2'' t 2' Q . W2 Предположим, что температуры рабочих жидкостей меняются по линейному закону, тогда t ' t '' t ' t '' Q K F 1 1 2 2 . 2 2 Подставляя в это уравнение вместо t1'' и t 2'' их значения, получаем Q ' ' Q t 2' t 2' t1 t1 W1 W2 Q K F 2 2 K F t ' Q t ' Q , 2 1 2W 2W2 1 или Q Q Q t1' t 2' , KF 2W1 2W2 откуда t1' t 2' Q . 1 1 1 K F 2W1 2W2 Зная количество теплоты Q , можно определить по формулам конечные температуры t1'' и t 2'' . Имея данные: t1' 98C ; t 2' 13C ; K 28,2 Вт ; F 26,79 м 2 ; 2 м K 4186 1360,282 1581,71 Вт / С 3600 0,24 4186 11921 W2 c 2 G 2 3326,75 Вт / С 3600 W1 c1 G1 находим t1' t 2' 98 13 48743,46 Вт 1 1 1 1 1 1 K F 2W1 2W2 28,2 26,79 2 1581,71 2 3326,75 Q 48743,46 t1'' t1' 98 67,18С W1 1581,71 Q 48743,46 t 2'' t 2' 13 27,65С W2 3326,75 Q Определим погрешность температур: 10 68,5 67,18 100 1,93% 68,5 27 27,5 t 2'' 100 1,85% 27 t1'' Список Литературы 1. Методические указания к курсовой работе «Расчет теплообменных аппаратов», 1993г. 11 2. 3. 4. 5. Исаченко В.П. Теплопередача. Учебник для вузов. М., Энергия, 1975г. Михеев М.А. Основы теплопередачи. М., Госэнергоиздат, 1956г. Нащокин В.В. Техническая термодинамика и теплопередача. Учеб. Пособие для неэнергетических специальностей вузов. М., Высшая школа, 1975г. Лебедев П.Д. Теплообменные, сушильные и холодильные установки Учеб. Для студентов технических вузов. М., Энегрия, 1972г. 12