Вопросы для самоконтроля по теме: «Седиментационный

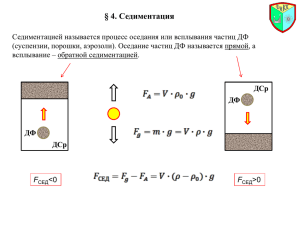
Вопросы для самоконтроля
низкодисперсных порошков»
по
теме:
«Седиментационный
анализ
1. Что такое седиментационная устойчивость коллоидных систем? В чем состоит
явление седиментации?
Седиментация (осаждение) — направленное движение частиц в поле действия
гравитации или центробежных сил вместе с жидкостью или газом.
Скорость седиментации зависит от массы, размера, формы и плотности вещества
частицы, а также от вязкости и плотности среды, а также от ускорения силы тяжести и
действующих на частиц центробежных сил.
В поле гравитационных сил седиментируют частицы грубодисперсных систем; в
поле центробежных сил возможна седиментация коллоидных частиц и макромолекул.
Седиментацию используют в промышленности при обогащении полезных
ископаемых, различных продуктов химической и нефтехимической технологии, при
водоочистке и др.
Седиментация в центрифугах и ультрацентрифугах, а также в гравитационном поле
лежит в основе седиментационного анализа.
Седиментационная устойчивость - это способность дисперсной системы сохранять
неизменным во времени распределение частиц по объему системы, т.е. способность
системы противостоять действию силы тяжести.
2. Какой закон лежит в основе седиментационного анализа?
В основе седиментационного анализа лежит закон Стокса, согласно которому
определяется сила вязкого сопротивления среды f, противодействующая осаждению
частиц.
Седиментационный анализ дисперсных систем основан на выше изложенном
уравнении, которое позволяет определить размеры частиц дисперсной фазы по скорости
их осаждения под действием силы тяжести. Уравнение применимо для определенных
размеров частиц с радиусами r= 10-7 – 10-4 м. Для осаждения частиц такого размера
применим закон Стокса. В дисперсных системах с более крупными частицами начинается
турбулизация жидкости из-за ускоренного движения частиц и уравнение Стокса
становится неприменимым.
3. Напишите уравнение седиментации для сферических частиц в поле земного
тяготения. От каких свойств среды зависит константа этого уравнения?
Это уравнение справедливо при условии сферической формы частиц и их
независимого движения друг от друга Поэтому дня седиментационного анализа
применяются сильно разбавленные системы, в которых можно пренебречь изменением
скорости движения частиц в результате их столкновения В большинстве рентных систем
частицы имеют неправильную форму. В этом случае по уравнению рассчитывается так
называемый эквивалентный радиус, то есть радиус частиц сферической формы,
оседающих с такой же скоростью.
Константа этого уравнения зависит от вязкость и плотности дисперсионной среды
и от скорости движения частицы.