Способы работы с обыкновенными дробями Основное свойство дроби Сравнение обыкновенных дробей

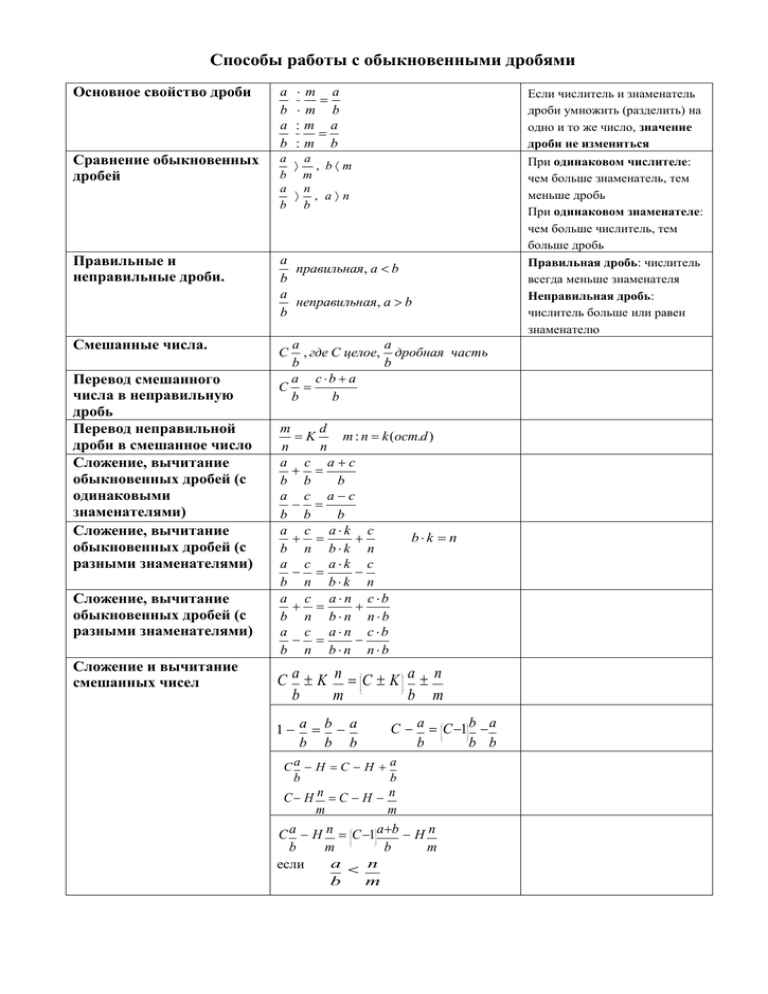
Способы работы с обыкновенными дробями
Основное свойство дроби
a
b
a
b
m a

m b
:m a

:m b
Если числитель и знаменатель
дроби умножить (разделить) на
одно и то же число, значение
дроби не измениться
Сравнение обыкновенных
дробей
a а
 , bm
b m
a n
 , an
b b
Правильные и
неправильные дроби.
a
правильная, а  b
b
a
неправильная, а  b
b
При одинаковом числителе:
чем больше знаменатель, тем
меньше дробь
При одинаковом знаменателе:
чем больше числитель, тем
больше дробь
Правильная дробь: числитель
всегда меньше знаменателя
Неправильная дробь:
числитель больше или равен
знаменателю
Смешанные числа.
Перевод смешанного
числа в неправильную
дробь
Перевод неправильной
дроби в смешанное число
Сложение, вычитание
обыкновенных дробей (с
одинаковыми
знаменателями)
Сложение, вычитание
обыкновенных дробей (с
разными знаменателями)
Сложение, вычитание
обыкновенных дробей (с
разными знаменателями)
Сложение и вычитание
смешанных чисел
a
а
, где С целое, дробная часть
b
b
a с b  a
С 
b
b
С
m
d
K
m : n  k (ост.d )
n
n
a с ac
 
b b
b
a с ac
 
b b
b
a с ak c
bk  n
 

b n bk n
a с ak c
 

b n bk n
a с a n c b
 

b n bn nb
a с a n c b
 

b n bn nb
СаK nCK a n
b
m
b m










C  a  C 1 b  a
b
b b
1 a  b  a
b b b





Сa  H  C  H  a
b
b
С H n  C  H  n
m
m
С a  H n  C 1 a b  H n
b
m
b
m
a  n
если
b
m














