Выполнила Мустафина Элина, гр. 09

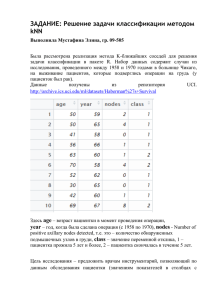
ЗАДАНИЕ: Средства оценки эффективности
методов бинарной классификации
Выполнила Мустафина Элина, гр. 09-505 (2)
Пусть перед нами поставлена задача классификации, которую мы будет решать 3-мя
методами:
1. методом KNN
2. методом naïve Bayes
3. методом Decision Tree
В качестве исходных данных были использованы данные из репозитория UCI.
http://archive.ics.uci.edu/ml/datasets/Haberman%27s+Survival
Набор данных содержит случаи из исследования, проведенного между 1958 и 1970 годами
в больнице Чикаго, на выживание пациентов, которые подверглись операции на грудь (у
пациенток был рак). Всего в выборке содержится информация о 305 пациентках.
В обучающей выборке содержатся данные о 157 пациентках, в тестовой – о 148
пациентках.
Рис.1. Исходные данные
Здесь age – возраст пациентки в момент проведения операции,
year – год, когда была сделана операция (с 1958 по 1970), nodes - Number of positive
axillary nodes detected, т.е. это – количество обнаруженных подмышечных узлов в груди,
class – значение переменной отклика, 1 – пациентка прожила 5 лет и более, 2 – пациентка
скончалась в течение 5 лет.
Цель исследования – предложить врачам инструментарий, позволяющий по данным
обследования пациентки (значениям показателей в столбцах с номерами 1 – 3)
спрогнозировать продолжительность жизни пациенток, перенесших операцию.
Таким образом, мы имеем задачу бинарной классификации, поскольку классов всего 2
(«1» и «2»).
Данная задача была решена 3-мя различными методами. Результаты были следующими:
kNN
Наивный Байес
Общее число ошибок = 18,2%
Общее число ошибок = 17,6%
Decision Tree
Общее число ошибок = 33%
Проанализируем полученные результаты:

(Survived, Survived) – содержит так называемые TN (True Negative) прогнозы, т.е.
те случаи, когда пациентка относится к классу Survived (т.е. проживших после
операции 5 и более лет), и метод правильно определил класс.



(Survived, Died) – содержит так называемые FN (False Negative) прогнозы, т.е. это
количество пациенток, которых метод отнес к прожившим 5 и более лет ошибочно,
т.е. на самом деле пациентки скончались в течение 5 лет.
(Died, Survived) – содержит так называемые FP (False Positive) прогнозы, т.е. это
количество пациенток, которых метод ошибочно отнес к умершим в течение 5 лет.
(Died, Died) – содержит так называемые TP (True Positive) прогнозы, т.е. это
количество пациенток, которых метод верно отнес к классу «Died», т.е. эти
пациентки действительно скончались в течение 5 лет после проведения операции.
Теперь нужно оценить эффективность каждого метода.
При анализе чаще оперируют не абсолютными показателями, а относительными – долями
(rates), выраженными в процентах:
Доля истинно - положительных примеров (True Positives Rate):
TPR=
𝐓𝐏
∗ 𝟏𝟎𝟎%
𝐓𝐏+𝐅𝐍
Доля ложно - положительных примеров (False Positives Rate):
FPR=
𝐅𝐏
∗ 𝟏𝟎𝟎%
𝐓𝐍+𝐅𝐏
Введем еще два определения: чувствительность и специфичность модели. Ими
определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) – это и есть доля истинно положительных случаев:
Se =TPR=
𝐓𝐏
𝐓𝐏+𝐅𝐍
∗ 𝟏𝟎𝟎%
Специфичность (Specificity) – доля истинно отрицательных случаев, которые были
правильно идентифицированы моделью:
Sp =
𝐓𝐍
𝐓𝐍+𝐅𝐏
Заметим, что FPR=100-Sp.
Попытаемся разобраться в этих определениях.
∗ 𝟏𝟎𝟎%
Модель с высокой чувствительностью часто дает истинный результат при наличии
положительного исхода (обнаруживает положительные примеры). Наоборот, модель с
высокой специфичностью чаще дает истинный результат при наличии отрицательного
исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины –
задачи диагностики заболевания, где модель классификации пациентов на больных и
здоровых называется диагностическим тестом, то получится следующее:

Чувствительный диагностический тест проявляется в гипердиагностике – максимальном
предотвращении пропуска больных;

Специфичный диагностический тест диагностирует только доподлинно больных. Это
важно в случае, когда, например, лечение больного связано с серьезными побочными
эффектами и гипердиагностика пациентов нежелательна.
Определим меру точности (P, precision) как:
Мера точности характеризует, сколько полученных от классификатора положительных
ответов являются правильными. Чем больше точность, тем меньше число ложных
попаданий.
Мера точности, однако, не дает представление о том, все ли правильные ответы вернул
классификатор. Для этого существует так называемая мера полноты (R, recall):
Мера полноты характеризует способность классификатора «угадывать» как можно
большее число положительных ответов из ожидаемых. Заметим, что ложноположительные ответы никак не влияют на эту метрику.
Precision и Recall дают довольно исчерпывающую характеристику классификатора,
причем «с разных углов». Обычно приходится все время балансировать между двумя
этими метриками. Если вы пытаетесь повысить Recall, делая классификатор более
«оптимистичным», это приводит к падению Precision из-за увеличения числа ложно положительных ответов. Если же вы пытаетесь сделать его более «пессимистичным»,
например, строже фильтруя результаты, то при росте Precision это вызовет одновременное
падение Recall из-за отбраковки какого-то числа правильных ответов. Поэтому удобно для
характеристики классификатора использовать одну величину, так называемую метрику F1:
ROC – кривая.
ROC – кривая -(англ. receiver operating characteristic, рабочая характеристика
приёмника) — график, позволяющий оценить качество бинарной классификации,
отображает соотношение между долей объектов от общего количества носителей
признака, верно классифицированных, как несущих признак, (англ. true positive rate, TPR,
называемой чувствительностью алгоритма классификации) и долей объектов от общего
количества объектов, не несущих признака, ошибочно классифицированных, как несущих
признак (англ. false positive rate, FPR, величина 1-FPR
называется специфичностью алгоритма классификации). Также известна как кривая
ошибок. Анализ классификаций с применением ROC-кривых называется ROC-анализом.
Количественную интерпретацию ROC даёт показатель AUC (англ. area under ROC
curve, площадь под ROC-кривой) — площадь, ограниченная ROC-кривой и осью доли
ложных положительных классификаций. Чем выше показатель AUC, тем качественнее
классификатор, при этом значение 0,5 демонстрирует непригодность выбранного метода
классификации (соответствует случайному гаданию).
Теперь построим ROC-кривые для наших данных.
Для этого будем использовать пакет «ROCR», который представляет собой пакет системы
R для оценки и визуализации качества классификации на два класса. Есть возможность
подсчета различных мер качества классификации и построения 2D графиков для
отдельных мер или для зависимости одной меры от другой.
Для использования средств данного пакета необходимы данные об истинных (labels) и
предсказанных каким-либо образом (predictions) метках классов выборки объектов.
Начнем с метода KNN:
Вызовем метод KNN:
Здесь при вызове метода KNN нужно указать параметр prob=TRUE для того, чтобы в
переменной data_test_pred_knn были не предсказанные номера классов для тестовой
выборки, а вероятности попадания в предсказанный класс.
data_test_pred_knn <- knn(train = data_train, test = data_test,cl =
data_train_class, k=12,prob=TRUE)
prob_knn <- attr(data_test_pred_knn, "prob")
Функция для создания объекта класса prediction из исходных данных.
pred_knn <- prediction(predictions =
prob_knn,
labels = data_test_class)
Здесь predictions - вектор, матрица, список или фрейм, содержащий предсказанные
значения переменной отклика для объектов тестовой выборки, labels - вектор, матрица,
список или фрейм, содержащий истинные значения переменной отклика для объектов
тестовой выборки.
Функция для создания объекта класса performance из объекта класса prediction.
Объекты этого класса предназначены для хранения результатов оценки качества
классификации в форме предназначенной для построения графика.
perf_knn <- performance(pred_knn, measure = "fpr", x.measure = "tpr")
Здесь pred_knn - объект класса prediction., measure - мера качества, используемая для оси у
(в нашем случае это true positive rates) , x.measure - мера качества, используемая для оси х
(в нашем случае это false positive rates).
Функция для визуализации объекта класса performance.
plot(perf_knn, main = "ROC curve",
col = "red", lwd = 3)
abline(a = 0, b = 1, lwd = 2, lty = 2)
В результате получили:
Теперь проделаем то же самое для метода Байеса и метода деревьев решений. Затем
сравним результаты:
Для метода наивного Байеса:
data_classifier <- naiveBayes(data_train, data_train_class)
data_test_pred <- predict(data_classifier, data_test,type="raw")
pred_nb <- prediction(predictions =
data_test_pred[,2],
labels = data_test_class)
perf_nb <- performance(pred, measure = "tpr", x.measure = "fpr")
plot(perf_nb, main = "ROC curve for naive Bayes",
col = "blue", lwd = 3)
abline(a = 0, b = 1, lwd = 2, lty = 2)
Результат:
Для метода деревьев решений:
data_model<-C5.0(data_train,data_train_class)
data_test_pred_trees<-predict(data_model,data_test,type="prob")
pred_tr <- prediction(predictions =
data_test_pred_trees[,2],
labels = data_test_class)
perf_tr <- performance(pred_tr, measure = "tpr", x.measure = "fpr")
plot(perf_tr, main = "ROC curve for Decision Tree",
col = "violet", lwd = 3)
abline(a = 0, b = 1, lwd = 2, lty = 2)
Результат:
Теперь совместим все кривые на одном графике:
Видно, что самый хороший результат показал метод KNN, а самый худший результат
показал метод деревьев решений, т.е. в нашем случае метод деревьев является
непригодным для классификации (соответствует случайному гаданию).
Теперь посмотрим, каково значение AUC для всех моделей:

Decision tree

KNN

naïve Bayes
Сравнивая показатели AUC для каждой модели, приходим к выводу, что лучшим методом
для решения конкретной задачи классификации является метод KNN.
В литературе иногда приводится следующая экспертная шкала для значений AUC, по
которой можно судить о качестве модели:
Интервал AUC
Качество модели
0.9-1.0
0.8-0.9
0.7-0.8
0.6-0.7
0.5-0.6
Отличное
Очень хорошее
Хорошее
Среднее
Неудовлетворительное