работу полностью

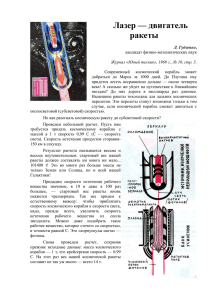
Научная основа полетов в космос (применение формулы Циолковского).
Выполнил: Арганаиди А.С., 11 класс, ГБОШИ РФМЛИ.
Научный руководитель: Кесаев В.И., доцент СОГУ.
Заслуга Циолковского не в формуле, а в том, что он первый увидел в ней возможность выхода человека в
мировое пространство.
Б.В. Раушенбах.
Предисловие.
Мысль о путешествиях на другие планеты, о странствии в межзвездных пустынях еще недавно
была только мечтой. Но сейчас нет уже сомнений, что, подобно тому, как авиация из заманчивой
грезы превратилась в повседневную действительность, так и в недалеком будущем осуществится
мысль о полетах в дальний космос.
Рождение космонавтики, как науки, произошло в 1987 году. В этом году была опубликована
магистерская диссертация И.В Мещерского, содержащая фундаментальное уравнение динамики
тел переменной массы. Уравнение Мещерского дало космонавтике «вторую жизнь»: теперь в
распоряжении ракетостроителей появились точные формулы, которые позволяли создавать ракеты,
основываясь не на опыте предыдущих наблюдении, а на точных математических расчетах.
Но наибольшую известность в космонавтики получило не уравнение Мещерского, а
уравнение Циолковского. Оно представляет собой частный случай уравнения Мещерского.
К. Э. Циолковского можно назвать отцом космонавтики. Он был первым, кто увидел в ракете
средство для покорения человеком космоса. До Циолковского на ракету смотрели как на игрушку
для развлечений или как на один из видов оружия. Заслуга К. Э. Циолковского состоит в том, что
он теоретически обосновал возможность покорения космоса при помощи ракет, вывел формулу
скорости движения ракеты, указал на критерии выбора топлива для ракет, дал первые
схематические чертежи космических кораблей, привёл первые расчеты движения ракет в поле
тяготения Земли и впервые указал на целесообразность создания на орбитах вокруг Земли
промежуточных станций для полётов на другие тела Солнечной системы.
Цели и задачи данной работы:
1. Получить нерелятивистское уравнение реактивного движения.
2. Получить уравнение реактивного движения в гравитационном поле.
3. Получить релятивистское уравнение реактивного движения.
4. Вычислить коэффициент полезного действия ракеты.
5. Изучить принцип работы фотонного двигателя. Получить уравнение, описывающее
движение фотонной ракеты.
Реактивное движение.
Среди великих технических и научных достижений XX века одно из первых мест, несомненно,
принадлежит ракетам и теории реактивного движения. Годы второй мировой войны привели к
быстрому совершенствованию конструкций реактивных аппаратов. На полях сражений появились
пороховые ракеты, но уже на более калорийном бездымном тротил-пироксилиновом порохе
(«катюши»). Были созданы самолеты с воздушно-реактивными двигателями, беспилотные
самолеты с пульсирующими воздушно-реактивными двигателями (Фау-1) и баллистические
ракеты с дальностью полета до 300 км (Фау-2).
Схема
простейшего
жидкостного
реактивного
двигателя представлена на рисунке. Через форсунки
происходит подача жидкого горючего и окислителя в
камеру
горения.
Подача
компонентов
топлива
рассчитывается таким образом, чтобы обеспечить
полное сгорание. В камере сгорания происходит
воспламенение топлива, и продукты горения —
горячие газы — с большой скоростью выбрасываются
через сопло. Окислитель и горючее помещаются в
специальных баках, располагающихся на ракете или
самолете. Для подачи окислителя и горючего в камеру сгорания применяют турбонасосы.
Струя горячих газов, выбрасываемая из сопла реактивного двигателя, создает реактивную силу,
действующую на ракету в сторону, противоположную
скорости
частиц струи. Величина реактивной силы равняется произведению массы
отбрасываемых в одну секунду газов на относительную скорость (это будет показано ниже при
выводе уравнения Мещерского). Если скорость измерять в метрах в секунду, а массу секундного
расхода через вес частиц в килограммах,
разделенных
на
ускорение
силы
тяжести, то
реактивная сила будет получаться в килограммах. Возьмем, например, реактивный двигатель, в
котором каждую секунду сгорает 4,9 кг топлива. Пусть относительная скорость отбрасываемых
частиц (продуктов сгорания) будет 2000
м
, тогда реактивная сила, которую обозначим через Ф ,
с
будет равна
Ф
4,9
 2000  1000 кг.
9,8
У немецкой ракеты Фау-2 весовой секундный расход составляет в среднем 127,4 кг. Скорость
истечения продуктов сгорания из сопла двигателя равна 2000 м/сек. Реактивная сила в этом случае
равна
Ф
127,4
 2000  26000 кг.
9,8
Приведенные примеры показывают, что реактивная сила тем больше, чем больше секундный
расход топлива и чем больше относительная скорость отбрасывания частиц.
Уравнения Мещерского и Циолковского.
Уравнения движения тел с переменной массой являются следствиями законов Ньютона. Тем не
менее, они представляют большой интерес, главным образом, в связи с ракетной техникой.
Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество
(газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но
противоположно направленной силой, в свою очередь, действует на ракету и сообщает ей
ускорение в противоположном направлении. Если нет внешних сил, то ракета вместе с
выброшенным веществом является замкнутой системой. Импульс такой системы не может
меняться во времени. На этом положении и основана теория движения ракет.
Получим уравнение движения материальной точки с переменной массой на примере движения
ракеты, следуя изложению из [1]. Пусть m – масса ракеты в некоторый момент времени, а v – ее
скорость в тот же момент времени. Спустя время dt масса ракеты и ее скорость получат
приращения dm и dv, за счет того, что будет выброшена масса газов dmгаз со скоростью vгаз. Тогда
изменение суммарного импульса системы ракета плюс газы, на которую действует внешняя
постоянная сила F, будет равно
(m+dm)(𝑣⃗+d𝑣⃗)+ dmгаз 𝑣газ
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ – m𝑣
⃗⃗⃗⃗= 𝐹⃗ dt.
Учитывая, что dmгаз +dm=0 и 𝑢
⃗⃗= 𝑣газ
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗– 𝑣⃗ (𝑢
⃗⃗ – скорость истечения газов относительно ракеты),
раскрываем скобки, пренебрегаем слагаемым dmd𝑣⃗ и в итоге получаем:
⃗⃗
𝑑𝑣
𝑑𝑡
md𝑣⃗= 𝑢
⃗⃗dm+𝐹⃗ dt <=> m
= 𝑢
⃗⃗
𝑑𝑚
+𝐹⃗ .
𝑑𝑡
По форме это уравнение похоже на второй закон Ньютона. Однако масса ракеты m здесь
непостоянна из-за потери вещества. К внешней силе F добавляется дополнительное слагаемое
𝑢
⃗⃗
𝑑𝑚
𝑑𝑡
, называемое реактивной силой, с которой выброшенные газы действуют на ракету. Это есть
уравнение И.В. Мещерского.
Применим уравнение Мещерского для полета ракеты, когда на нее не действуют внешние силы,
т.е. F=0. Тогда мы получим:
⃗⃗
𝑑𝑣
m 𝑑𝑡 = 𝑢
⃗⃗
𝑑𝑚
𝑑𝑡
(1.1)
Пусть ракета движется прямолинейно в направлении, противоположном направлению движению
газов. Если принять направление полета за положительное, то уравнение 1.1 в скалярной форме
выглядит так:
𝑑𝑣
𝑑𝑚
𝑢
=–𝑚 .
Будем для простоты полагать, что скорость u является постоянной, тогда:
v =– u ∫
𝑑𝑚
𝑚
=– u 𝑙𝑛 𝑚 +C.
Значение постоянной C можно найти из следующих соображений: в начальный момент времени
скорость ракеты v=0, а ее масса m равна начальной массе m0, отсюда C= u ln m0. Значит,
v = u ln m0/m , или m=m0exp(-v/ u ).
Полученное уравнение есть формула Циолковского. Она получена для нерелятивистских
движений, т.е. для случаев, когда v и vотн очень малы по сравнению со скоростью света. Но ее
можно обобщить на случай движения со скоростями, близкими к скорости света.
Обозначим за v и m – масса покоя и скорость ракеты в произвольный момент времени, mгаз и vгаз
– те же величины для газов, образовавшихся из ракеты к этому моменту времени. Газы, уже
покинувшие ракету, на ее движение влияния не оказывают, поэтому можно будет принять mгаз=0.
Но газы образуются непрерывно, поэтому dmгаз≠0. Запишем законы сохранения импульса и
энергии:
⃗⃗
𝑚𝑣
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
𝑚газ 𝑣газ
+
𝑣
√1−( )2
𝑐
𝑉газ 2
)
𝑐
= const,
√1−(
𝑚
𝑚 газ
+
𝑣
√1−( )2
𝑐
𝑉газ 2
)
𝑐
= const.
√1− (
Дифференцируя 1-ое уравнение, учитывая 2-ое, и принимая в итоге mгаз=0, получим:
⃗⃗
𝑚𝑑𝑣
𝑣
√1−( )2
𝑐
+ (𝑣⃗- 𝑢
⃗⃗)
𝑑𝑚
𝑣
√1−( )2
=0. (1)
𝑐
По релятивистскому закону сложения скоростей получаем:
vгаз=
𝑣− 𝑢
𝑣 𝑢,
(2)
1— 2
𝑐
Исключая из уравнения 1 vгаз с помощью уравнения 2, получим:
𝑢 𝑑𝑚
.
𝑚
dv/(v2—c2)= 𝑐 2
Для простоты полагая скорость u постоянной и интегрируя, находим, что:
1+𝑎
m0/m = (1−𝑎)
𝑐/2𝑢
, (3)
𝑣
с
где a= .
Уравнение 3 есть релятивистская формула Циолковского. Разумеется, она должна содержать
нерелятивистскую формулу как предельный случай. Проверим это. Выражение
стремится к бесконечности, a – к нулю.
1+𝑎 𝑐/2𝑢
lim (1−𝑎)
𝑎→0
=
lim (1+𝑎)𝑐/2𝑢
𝑎→0
lim (1−𝑎)𝑐/2𝑢
𝑎→0
.
𝑐
2𝑢
будет
𝑣 2𝑢 𝑐/2𝑢
)
= 𝑐lim
2𝑢
→∞
lim (1 + 𝑎)𝑐/2𝑢 = 𝑐lim (1 + 𝑐
𝑎→0
→∞
2𝑢
𝑘 𝑥∗𝑘/𝑘
= lim (1 + 𝑥 )
𝑥→∞
2𝑢
𝑣 2𝑢 𝑐/2𝑢
)
= lim
2𝑢
𝑥→∞
(1 + 𝑐
𝑣 1 𝑥
(1 + 2𝑢 𝑥) =
= 𝑒 𝑘 = 𝑒 𝑣/2𝑢 .
Аналогично получаем, что:
lim (1 − 𝑎)𝑐/2𝑢 = 𝑒 −𝑣/2𝑢 .
𝑎→0
В итоге получаем:
1+𝑎 𝑐/2𝑢
lim (1−𝑎)
𝑎→0
= 𝑒 𝑣/𝑢
<=> m0/m=𝑒 𝑣/𝑢 ,
Что и требовалось доказать.
Уравнение реактивного движения в поле тяжести.
Используя уравнение Мещерского, попробуем описать движение ракеты в поле тяжести, т.е.
найдем связь между массой ракеты m(t), достигнутой ею скоростью v(t) и временем t согласно
изложению в [1]. Для простоты будем считать, что ракета движется вертикально вверх в поле
тяжести Земли, что скорость газовой струи относительно ракеты u является постоянной. Также,
пренебрежем сопротивлением воздуха и изменением ускорения свободного падения g с высотой.
Как было показано выше:
𝑑𝑣
m 𝑑𝑡 = -u
𝑑𝑚
–mg.
𝑑𝑡
(уравнение Мещерского в скалярной форме).
Переписывая это уравнение в виде
𝑑
m𝑑𝑡 (𝑣 + 𝑔𝑡)= -u
𝑑𝑚
𝑑𝑡
<=>
𝑑(𝑣+𝑔𝑡)
𝑑𝑚
𝑢
= -𝑚
Последнее уравнение имеет такой же вид, как и уравнение 1.1. Поэтому просто заменим (v+gt) за
неизвестное, заменяя им в уравнении 1.1 v. Тогда получим:
m0/m = exp(
𝑣+𝑔𝑡
𝑢
) (4)
Т.е.
v(t)= u ln(m0/m) – gt.
Попробуем теперь найти, какую массу газов μ(t) должна выбрасывать ракета, чтобы оставаться
неподвижной в поле тяжести Земли. Его легко найти из условия неподвижности ракеты (
𝑑𝑣
𝑑𝑡
= 0).
𝑑𝑚
Очевидно, величина μ равна – 𝑑𝑡 .
μ= –
𝑑𝑚 𝑚𝑔
= 𝑢 .=
𝑑𝑡
(m0g/u) exp(-gt/ u).
Полезное действие ракеты.
Подсчитаем, какую долю энергии горючего ракета переводит в полезную механическую работу.
Условимся называть коэффициентом полезного действия ракеты η отношение кинетической
энергии ракеты в конце разгона к кинетической энергии выброшенных газов. Положим начальная
и конечная массы ракеты соответственно m0 и m, время работы двигателей ракеты τ, массовый
расход топлива равен μ, скорость истечения газов относительно ракеты постоянна и равна u. Тогда
легко найти конечную скорость ракеты, используя формулу Циолковского. Зная, что
v = u ln m0/m,
Находим, что конечная кинетическая энергия ракеты равна
E1=
𝑚𝑢2
𝑀2
ln
.
2
𝑀0
Теперь посчитаем полную кинетическую энергию выброшенных газов в системе отсчета,
связанной с Землей. Она будет равна
E2=
𝑑[μt(v−u)2 ] 1
=2
𝑑𝑡
𝑑𝑣
μ(v − u)2 + μt(v-u) 𝑑𝑡 .
Как было показано выше,
𝑑𝑣 = –𝑢
𝑑𝑚
𝑚
𝑑𝑣
<=> 𝑑𝑡 =−
𝑢 𝑑𝑚
𝑚 𝑑𝑡
<=>
𝑑𝑚
𝑚 𝑑𝑣
=− 𝑢 𝑑𝑡
𝑑𝑡
.
Используя формулу Циолковского, получаем
𝑑𝑚
=
𝑑𝑡
𝑑𝑣
– m0 exp(-v/u) 𝑢𝑑𝑡= – μ.
Тогда
𝑑𝑣
𝑑𝑡
𝑢μ
= 𝑀0exp(v/u).
Учитывая это, получаем, что
τ 𝑑𝐸
E2= ∫0
𝑑𝑡
μ
τ
dt=− ∫0 (𝑣 − 𝑢)2 𝑑𝑡 +
2
μ2 u τ
∫ 𝑡(𝑣
𝑀0 0
− 𝑢)exp(𝑣/𝑢)𝑑𝑡.
Учтем то, что
v(t) = −𝑢 ln
𝑀0−μt
.
𝑀0
Тогда, избавляясь от значения v и после несложных преобразований, получим, что
E2=
𝑀0𝑢2
𝑀2
(ln 𝑀0
2
𝑀
+ 2 ln 𝑀0).
Находим отношение энергии ракеты к энергии газов:
𝑀
η=
𝑀 ln𝑀0
.
𝑀0 ln 𝑀 +2
𝑀0
Заметим, что это очень небольшой кпд. Например, используя полученное выражение, вычисли кпд
ракеты Союз-2.1в. Масса полезного груза для нее обычно – 2,8 тонны, а вся стартовая масса – 157
тонн. Подставляя эти значения в выражение для кпд, получим, что он приблизительно равен 3,5%.
Применение формулы Циолковского.
Из формулы Циолковского следует:
а). Скорость движения ракеты в конце работы двигателя (в конце активного участка полета) будет
тем больше, чем больше относительная скорость отбрасываемых частиц. Если относительная
скорость истечения удваивается, то и скорость ракеты возрастает в два раза.
б). Скорость ракеты в конце активного участка возрастает, если увеличивается отношение
начальной массы (веса) ракеты к массе (весу) ракеты в конце горения. Однако здесь зависимость
более сложная, она дается следующей теоремой Циолковского:
«Когда масса ракеты плюс масса взрывчатых веществ, имеющихся в реактивном приборе,
возрастает в геометрической прогрессии, то скорость ракеты увеличивается в прогрессии
арифметической».
Этот закон можно выразить двумя рядами чисел:
Относительная
масса (вес) 
M0
MS
Относительная
скорость ракеты
27=
2
22=4
23=8
24=16
25=32
26=64
128
1
2
3
4
5
6
7
Из теоремы и пояснений Циолковского видно, что «скорость ракеты далеко не пропорциональна массе, взрывчатого материала: она растет весьма медленно, но беспредельно».
Из формулы Циолковского следует весьма важный практический результат: для получения
возможно больших скоростей ракеты в конце работы двигателя нужно увеличивать относительные
скорости отбрасываемых частиц и увеличивать относительный запас топлива.
Простая формула Циолковского позволяет путем элементарных вычислений устанавливать
исполнимость того или другого задания. В самом деле, пусть, например, вы хотите создать
одноступенчатую ракету для полета на Марс. Вы располагаете двигателем, имеющим относительную скорость отброса частиц, равную 2500
тяготения Земли нужна скорость 11,2
м
. Тогда, зная, что для преодоления поля
с
км
, можно найти необходимый относительный запас
с
топлива в ракете. Из формулы Циолковского имеем
11,2  2,3  2500  lg
M0
,
MS
или
lg
M0
 1,948.
MS
По таблицам десятичных логарифмов находим, что
M0
 88,
MS
т. е. суммарный вес конструкции ракеты, двигателя, вспомогательных механизмов и приборов
управления должен составлять немногим больше 1% стартового веса. Такую ракету сделать
невозможно. Если бы удалось увеличить относительную скорость истечения до 4850
формулы Циолковского легко найти, что в этом случае
lg
а следовательно,
M0
 1,
MS
м
, то из
с
M0
 10,
MS
т.е. вес ракеты без топлива должен составлять 10% ее стартового веса. Такую ракету можно
создать.
Формула Циолковского позволяет рассчитать запас топлива, необходимый для сообщения
ракете скорости v. Как видно, отношение начальной массы m0 к конечной массе ракеты равно
exp(v/u ). В таблице 1 приведены отношения начальной массы ракеты m0 к ее конечной массе m,
полученные с помощью нерелятивистской формулы (ее можно применять, например, для
движения ракет на химическом топливе).
Таблица 1.
v/ u
m0/m
v/ u
m0/m
v/ u
m0/m
v/ u
m0/m
1
2,72
4
54,6
7
1100
10
22000
2
7,39
5
148
8
2980
11
59900
3
20,1
6
403
9
8100
12
163000
Скорость истечения газов у современных ракет на химическом топливе составляет примерно 3–
4 км/с. Для сообщения ракете первой космической скорости, равной 8 км/с, отношение m0/m будет
равно
7,39 при скорости истечения газов 4 км/с. При скорости истечения 2 км/с это отношения
равно 54,6. Т.е. практически вся начальная масса ракеты приходится на топливо. Но и при
отношении m0/m, равном 7,39, масса топлива в несколько раз превосходит массу самой ракеты.
Технические трудности, связанные с достижением космических скоростей, решаются с помощью
многоступенчатых ракет, идея создания которых принадлежит Циолковскому.
Для межзвездных полетов космических кораблей ракеты на химическом топливе абсолютно
непригодны. Ближайшие к нам звезды находятся на расстоянии примерно 4 световых лет, поэтому
для межзвездной экспедиции приемлемой длительности необходимы скорости близкие к скорости
света. Формула Циолковского показывает, что для достижения таких скоростей, отношение m0/m
будет невообразимо большим:
Таблица2.
a=v/c
0,001
m0/m
a=v/c
m0/m
Релятивистская
Нерелятивистская
Релятивистская
Нерелятивистская
формула
формула
формула
формула
1,0690*1013
1,0686*1013
5,37*103327
1,62*103257
0,25
0,01
1,963*10130
1,942*10130
0,1
1,79*101307
7,64*101302
1/3
2,84*104515
8,81*104342
Результаты, приведенные в таблице, 2 наглядно показывают, как существенны релятивистские
эффекты. При скорости равной только 0,25c отношение m0/m≈5*103327 . На каждую полезную
тонну груза будет приходиться 5*103327 тонн топлива! Т.е. если полезная масса корабля всего лишь
1 кг, то масса топлива равна 5*103327 кг. Эта величина колоссальна, к примеру, масса нашей
галактики «всего-то» 3*1038.
Конечно, нет смысла говорить о движении фантастического корабля с массой, превышающей
массу нашей Метагалактики. Кроме того,
обычная теория движения ракет основана на
предположении, что импульс практически мгновенно передается ракете в целом. Это условие не
может выполняться для ракет очень больших размеров. Можно конечно придумать какой-нибудь
корабль, для которого оно выполняться будет, но, во всяком случае, примеры показывают, что
ракеты на химическом топливе к межзвездным полетам непригодны.
Для превращения ракеты в межзвездный корабль, нужно приблизить скорость струи к скорости
света. Так могло бы быть в фотонной ракете, для которой u=c, роль газовой струи для нее
выполняет световой пучок, излучаемый двигателем корабля. Реактивная сила в фотонной ракете
осуществлялась бы давлением света.
Принцип работы фотонного двигателя.
Для начала, поясним, что такое фотонный двигатель. Фотонный (или квантовый двигатель) есть
гипотетический двигатель, в котором бы источником энергии служило бы тело, излучающее свет.
Фотон, имея импульс, при истекании из двигателя создает реактивную силу. Теоретически,
фотонный двигатель может позволить развить скорости, близкие к скорости света. Однако
практическая разработка подобных двигателей дело отдаленного будущего.
Чаще всего обсуждаются и упоминаются в научно-фантастической литературе идеи создания
такого двигателя с использованием антивещества. Энтузиасты считают, что взаимодействие
вещества и антивещества позволяет перевести практически всю вступающую в реакции массу в
излучение.
Принцип работы фотонного двигателя следующий: в камеру подается вещество и антивещество.
В ходе аннигиляции появляются кванты света, которые направляются на стенку-зеркало, оказывая
на нее давление, вызывающее реактивную тягу.
На сегодняшний день идея фотонного двигателя далека от технического воплощения. Она
содержит ряд проблем, который пока что не удается решить даже теоретически.
Первая трудность, стоящая на пути осуществления классической фотонной ракеты – большая
относительная масса ракеты на старте. Для того, чтобы совершить полёт к другой звезде и
вернуться обратно, необходимо совершить четыре разгона (2 раза набирать скорость, и 2 раза
тормозить). Скорость, развиваемую в ходе полёта, можно оценить в 0,9 скорости света, тогда
стартовая масса превосходит конечную (по расчетам Зенгера) в 361 раз! Для современных ракет
это число порядка 30: для «Сатурна-5» - 3000 тонн/100 тонн=30, для «Протона» - 600 тонн/20
тонн=30.
Это
показывает,
насколько
будет
сложно
создать
подобную
ракету.
Вторая трудность связана с тем, что при реакции аннигиляции рождаются кванты излучения,
имеющие очень малую длину волны. При расчётах выясняется, что это будут гамма-кванты. Ещё
не
существует
способа
отражать
такие
кванты.
Наконец, существующие зеркала поглощают большую долю падающей на них энергии, поэтому
излучение двигателя просто испарит любое зеркало. Чтобы этого не произошло, пришлось бы
увеличивать диаметр зеркала, но тогда оно приобретёт гигантские размеры.
Для того, чтобы решить первую проблему, стоящую на пути создания фотонной ракеты,
Бурдаков и Данилов предложили использование внешней среды в качестве топлива. Идея
заключается в том, что теперь необходимо везти лишь половину горючего, т. е. антивещество,
которого нет в пространстве, находится на борту ракеты, а обычное вещество забирается
массозаборником из окружающей среды.
Для того, чтобы осуществлять сбор межзвёздного вещества, на 70% состоящего из водорода,
необходимо его ионизировать. Для этого предложено направлять вперед поток электромагнитного
излучения или электронов. Ионизованный водород собирается магнитным массозаборником,
представляющим собой конус диаметром 20 метров и длиной около 25, состоящий из витков
сверхпроводника. Современные материалы теряют сверхпроводимость при напряжённости
магнитного поля в массозаборнике. Поэтому предлагается использование металлического
водорода, или его сплава с лёгким металлом, охлаждаемого жидким гелием.
Решением второй и третьей проблем стала идея использования электронного зеркала. Суть в
том, что электронное зеркало можно сделать достаточно плотным, а удержание производить с
помощью магнитного поля.
Теперь, зная что, импульс излучения p связан с его энергией ε соотношением
p=cε, c – скорость света,
Посмотрим, как изменится формула Циолковского для фотонной ракеты.
Изменение энергии ракеты равно энергии образовавшегося излучения:
(m0 –
𝑚
√1−𝑎 2
) c2 = ε
Импульс ракеты равен импульсу излучения (по модулю):
𝑚𝑣
√1−𝑎2
= p.
Тогда,
(m0 –
𝑚
√1−𝑎2
) c2 –
𝑚𝑣𝑐
√1−𝑎2
= ε – cp=0.
Отсюда:
1+𝑎
mo/m = √1−𝑎 .
Легко заметить, что эту формулу легко получить, просто приняв в релятивистской формуле
Циолковского u= c.
Выводы:
В данной исследовательской работе получены релятивистская и нерелятивистская формулы
Циолковского для движения ракет в поле тяжести и в отсутствии его. Они имеют очень важное
практическое значение в космонавтике. При помощи этих уравнений можно решить многие
задачи, связанные с движением ракет.
На основании формулы Циолковского получено выражение для КПД ракеты. Показано, что он
имеет весьма небольшое значение для современных ракет на химическом топливе.
Так же показано, что для межзвездных полетов неприменимы ракеты на химическом топливе изза технических трудностей, связанных с большой массой необходимого топлива.
Изучен принцип работы фотонного двигателя, гипотетически способного позволить достичь
скоростей, близких к скорости света, и совершать межзвездные полеты. Получено уравнение,
описывающее движение фотонной ракеты.
Использованная литература:
1. Сивухин Д.В. Механика: Учебное пособие для вузов. – 3-е изд., 1989.
2. Бутиков Е.И., Быков А.А., Кондратьев А.С. Физика для поступающих в вузы: Учеб.
Пособие. – 3-е изд., 1991.
3. Журнал «Квант» 1990.
4. Бурдаков В.П., Данилов Ю.И. «Ракеты будущего» 1980.