ministerstvo_obrazovaniya_respubliki_belarus_
реклама

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«Белорусский государственный университет информатики
и радиоэлектроники»
Индивидуальная работа по курсу
«Теория вероятностей и математическая статистика»
Вариант № 1
Выполнила:
Проверил:
д.ф.-м.н., профессор
Аксенчик А. В.
Минск 2014
Задача №1.1
Подбрасываются две игральные кости. Определить вероятность того, что сумма выпавших
чисел равна восьми.
Решение
Событие А состоит в том, что сумма выпавших чисел будет равна восьми. Так как каждая
игральная кость имеет 6 различных цифр от 1 до 6, то число всех возможных исходов n опыта
равно числу размещений с повторением элементов из 6 по 2 :
n A62 6 2 36
Методом перебора всех возможных ситуаций можем найти, что существует 5 нужных
комбинаций чисел. Точнее, m будет равна 5.
Вероятность того, что сумма выпавших чисел будет равна восьми:
𝑃(𝐴) =
Ответ: 0,14.
𝑚
5
=
= 0.14
𝑛
36
Задача № 2.1
2
Приведена схема элементов, образующих цепь с одним входом и одним выходом.
Предполагается, что отказы элементов являются независимыми в совокупности событиями.
Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится
данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5, 6 соответственно равны q1 = 0.1, q2
= 0.2, q3 = 0.3, q4 = 0.4, q5 = 0.5, q6 = 0.6. Найти вероятность того, что сигнал пройдет со входа
на выход.
2
5
1
3
6
4
Решение
Схема состоит из трех участков. Первый содержит элемент 1, второй – элементы 2, 3 и 4, а
третий – элементы 5 и 6.
Введем события:
А1 – Элемент 1 исправлен;
А2 – Элемент 2 исправлен;
А3 – Элемент 3 исправлен;
А4 – Элемент 4 исправлен;
А5 – Элемент 5 исправлен;
А6 – Элемент 6 исправлен.
B – Сигнал проходит от точки a к точке b
C - Сигнал проходит от точки b к точке c
D - Сигнал проходит от точки c к точке d
G - Сигнал проходит от точки a к точке d
В нашем случае B = A1.
̅̅̅̅) = 0.9
𝑃(𝐵) = 𝑃(𝐴1) = 1 − 𝑃(𝐴1
Событие С сработает, если будут рабочие элементы 2, 3 и 4.
С = А2 + А3 + А4
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅
𝑃(𝐶) = 𝑃(𝐴2 + 𝐴3 + 𝐴4) = 1 − 𝑃(𝐴2
∗ 𝐴3 ∗ 𝐴4) = 1 − 𝑞2 ∗ 𝑞3 ∗ 𝑞4 = 1 − 0.024 = 0.976
Событие D – если работают элементы 5 и 6.
𝑃(𝐷) = 𝐴5 + 𝐴6
̅̅̅̅̅̅̅̅̅̅
𝑃(𝐷) = 𝑃(𝐴5 + 𝐴6) = 1 − 𝑃(𝐴5
∗ 𝐴6) = 1 − 𝑞5 ∗ 𝑞6 = 1 − 0.3 = 0.7
Событие G – если сигнал прошел через все блоки.
𝑃(𝐺) = 𝑃(𝐵 ∗ 𝐶 ∗ 𝐷) = 𝑃(𝐵) ∗ 𝑃(𝐶) ∗ 𝑃(𝐷) = 0.9 ∗ 0.976 ∗ 0.7 = 0.6
Ответ: 0,6.
Задача №3.1
3
На трех автоматических станках изготавливаются одинаковые детали. Известно, что 30%
продукции производится первым станком, 25% - вторым и 45% - третьим. Вероятность
изготовления детали, отвечающей стандарту, на первом станке равна 0,99, на втором – 0,988 и
на третьем – 0,98. Изготовленные в течение дня на трех станках нерассортированные детали
находятся на складе. Определить вероятность того, что взятая наугад деталь не соответствует
стандарту.
Решение
Событие А состоит в том, что попавшаяся деталь не соответствует стандарту.
Событие H1 – деталь принадлежит станку 1, все остальные станки исправны;
H2 – деталь принадлежит станку 2, все остальные исправны;
H3 – деталь принадлежит станку 3, все остальные исправны;
H4 – все станки неисправны;
H5 – неисправны только станки 1 и 2;
H6 – неисправны только станки 2 и 3;
H7 – неисправны только станки 1 и 3;
B1 – станок 1 исправен;
B2 – станок 2 исправен;
B3 – станок 3 исправен.
Сделаем следующие предположения:
̅̅̅̅ ⋂ 𝐵2 ⋂ 𝐵3
𝐻1 = 𝐵1
̅̅̅̅ ⋂ 𝐵2
̅̅̅̅ ⋂ 𝐵3
𝐻5 = 𝐵1
𝐻2 = 𝐵1 ⋂ ̅̅̅̅
𝐵2 ⋂ 𝐵3
𝐻6 = 𝐵1 ⋂ ̅̅̅̅
𝐵2 ⋂ ̅̅̅̅
𝐵3
𝐻3 = 𝐵1 ⋂ 𝐵2 ⋂ ̅̅̅̅
𝐵3
𝐻7 = ̅̅̅̅
𝐵1 ⋂ 𝐵2 ⋂ ̅̅̅̅
𝐵3
̅̅̅̅ ⋂ 𝐵2
̅̅̅̅ ⋂ 𝐵3
̅̅̅̅
𝐻4 = 𝐵1
̅̅̅̅ ⋂ 𝐵2 ⋂ 𝐵3) = 𝑃(𝐵1
̅̅̅̅) ∗ 𝑃(𝐵2) ∗ 𝑃(𝐵3) = (1 − 0.99) ∗ 0.988 ∗ 0.98 = 0.01
𝑃(𝐻1) = 𝑃 (𝐵1
̅̅̅̅) ∗ 𝑃(𝐵3) = 0.99 ∗ (1 − 0.988) ∗ 0.98 = 0.01
𝑃(𝐻2) = 𝑃(𝐵1) ∗ 𝑃(𝐵2
̅̅̅̅) = 0.02
𝑃(𝐻3) = 𝑃(𝐵1) ∗ 𝑃(𝐵2) ∗ 𝑃(𝐵3
𝑃(𝐻4) = 0.0000024
𝑃(𝐻5) = 0.0001176
𝑃(𝐻6) = 0.0002376
𝑃(𝐻7) = 0.0001976
По формуле полной вероятности, вероятность того, что взятая деталь окажется неисправной:
7
𝐴
𝑃(𝐴) = ∑ 𝑃(𝐻𝑖) ∗ 𝑃 ( ) = 0.04
𝐻𝑖
𝑖=1
Ответ:0,04
Задача №4.1
4
Вероятность изготовления стандартного изделия равна 0,95. Какова вероятность того, что среди
10 изделий не более одного нестандартного?
Решение
Вероятность того, что из n = 10 изделий k = 9 окажутся удачными, определим по формуле
Бернулли:
𝑛!
10!
∗ 𝑝𝑘 ∗ (1 − 𝑝)𝑛−𝑘 =
∗ 0.959 ∗ (1 − 0.95)1
(𝑛
𝑘! ∗ − 𝑘)!
9! 1!
= 10 ∗ 0.63 ∗ 0.05 = 0.31
𝑃(𝑛, 𝑘) = 𝐶𝑛𝑘 ∗ 𝑝𝑘 ∗ (1 − 𝑝)𝑛−𝑘 =
Ответ: 0.31
Задача №5.1
5
Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1,
x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно. Вычислить математическое
ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
xi
1
2
3
4
5
pi
0,2
0,2
0,2
0,2
0,2
Решение
1)
Математическое ожидание и дисперсию величины Х:
𝑀[𝑋] = ∑ 𝑥𝑖 𝑝𝑖 = 0.2 + 0.4 + 0.6 + 0.8 + 1 = 3
𝑖
𝑀[𝑋
2]
= ∑ 𝑥𝑖 2 𝑝𝑖 = 0.2 + 0.8 + 1.8 + 3.6 + 5 = 11.4
𝑖
𝐷[𝑋] = 𝑀[𝑋 2 ] − (𝑀[𝑋])2 = 11.4 − 9 = 2.4
2)
Построим ряд распределения СВ X:
xi
pi
1
2
3
4
5
>5
0,2
0,2
0,2
0,2
0,2
0
F ( xi )
0
0,2
0,4
0,6
0,8
1
𝑥 < 1,
𝐹(𝑥) = 0;
1 ≤ 𝑥 < 2,
𝐹(𝑥) = 0 + 0.2 = 0.2;
2 ≤ 𝑥 < 3,
𝐹(𝑥) = 0 + 0.2 + 0.2 = 0.4;
3 ≤ 𝑥 < 4,
𝐹(𝑥) = 0 + 0.2 + 0.2 + 0.2 = 0.6;
4 ≤ 𝑥 < 5,
𝐹(𝑥) = 0 + 0.2 + 0.2 + 0.2 + 0.2 = 0.8;
𝑥 > 5,
𝐹(𝑥) = 1;
Построим график функции распределения:
6
1.2
1
0.8
Fi 0.6
Series1
0.4
0.2
0
0
1
2
3
4
Xi
Задача №6.1
7
5
6
Случайная величина Х задана плотностью вероятности:
0, x a, x b,
f ( x)
( x, c), a x b.
Определить константу С, математическое ожидание, дисперсию, функцию распределения
величины Х, а также вероятность ее попадания в интервал , .
( x, c) с* | x 1 |; a 1; b 3; 0,5; 1,5.
Решение
1)
Вычислим константу c исходя из условия нормировки:
∞
3
∫ 𝑓(𝑥)𝑑𝑥 = ∫ 𝐶 ∗ |𝑥 + 1|𝑑𝑥 = 8𝐶 = 1 ⇔ 𝐶 = 1/8
−∞
2)
−1
Определим математическое ожидание СВ Х:
∞
3
𝑀[𝑋] = ∫ 𝑥 ∗ 𝑓(𝑥)𝑑𝑥 = 1/8 ∫ 𝑥 ∗ |𝑥 + 1|𝑑𝑥 = 5/3
−∞
3)
−1
Определим дисперсию СВ Х:
∞
𝐷[𝑋] = ∫ 𝑥2 𝑓(𝑥)𝑑𝑥 − 𝑀2 [𝑋] =
−∞
4)
11
3
−
25
3
= 8/ 9
Определим функцию распределения величины Х:
𝑥
𝑥
𝐹(𝑥 < −1) = ∫ 𝑓(𝑡)𝑑𝑡 = ∫ 0𝑑𝑡 = 0
−∞
−1
𝐹(−1 ≤ 𝑥 ≤ 3) = ∫
−∞
𝑥
1
∗ |𝑡 + 1|𝑑𝑡 = 1/16(𝑥 + 1)2 |𝑥 + 1|
8
−1
0𝑑𝑡 + ∫
−∞
−1
3
∞
𝐹(𝑥 > 3) = ∫ 0𝑑𝑡 + ∫ 1/8|𝑡 + 1|𝑑𝑡 + ∫ 𝑑𝑡 = 1
−∞
−1
1
x 1
0,
F ( x) 1 / 16( x 2) 2 | x 1 |, 1 x 3
1,
x3
5)
Определим вероятность попадания величины Х в заданный интервал , :
𝑃(−0.5 ≤ 𝑥 ≤ 1.5) = 𝐹(1.5) − 𝐹(−0.5) =
Ответ: C = 1/8, M[X] = 5/3, D[X] = 8/9, P(x) = -0.6
8
1
1
∗ |1.5 + 1| − (
) = −0.6
8
8(−0.5 + 1)
Задача №7.1
Случайная величина Х распределена равномерно на интервале [a,b]. Построить график
случайной величины Y=(X) и определить плотность вероятности g(y).
( X ) | x |, a 1, b 4.
Решение
1)
Построим график случайной величины Y | x | для x в интервале значений [1;4]
определим диапазон значений Y : Y [0;4]
2.5
2
1.5
Y
1
Series1
0.5
0
0
0.2
0.4
0.6
0.8
1
1.2
X
2)
3)
В зависимости от числа обратных функций выделим следующие интервалы для Y :
(; 0 ]
[0; 4 ]
k1 0 обратных функций не существует
k 2 1 𝜔1 (𝑦) = √𝑦 2
[4; ∞)
k3 0
Вычислим модули производных обратных функций:
|𝝎𝟏 (𝒚)| = |√𝒚𝟐 | = 𝟏
1
1
, 1 x 4
, 1 x 4
f ( x) 4 (1)
5
0, x 1, x 4
0, x 1, x 4
9
и
4)
Определим плотность вероятности величины Y :
0,
𝑦<0
𝑓𝑥 (√𝑦 2 ) ∗ 1, 0 ≤ 𝑦 ≤ 4
𝑔(𝑦) =
0, 𝑦 > 4
{
10
Задача №8.1
Двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными
прямыми линиями (рисунок 4) области B. Двухмерная плотность вероятности f(x,y) одинакова
для любой точки этой области B:
c,
f ( x, y )
0,
( x, y ) B ,
иначе.
Вычислить коэффициент корреляции между величинами X и Y.
Вариант
x1
x2
x3
x4
x5
x6
y1
y2
8.1
0
0
1
1
1
1
1
2
Решение
1)
Построим область B согласно координатам из таблицы и рисунку.
2.5
2
1.5
Series1
1
0.5
0
0
0.2
0.4
0.6
0.8
1
1.2
Проанализируем рисунок: область B на промежутке x [0;1] ограничена сверху прямой y 2
, снизу y 0
Следовательно, совместная плотность вероятности примет вид:
c, 0 y 2, 0 x 1
f ( x, y )
0, иначе.
11
2)
Найдём константу с из условия нормировки:
∞
∫
∞
2
1
∫ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ ∫ 𝐶𝑑𝑥𝑑𝑦 = 2𝐶 ⇔ 𝐶 = 1/2
−∞ −∞
0
0
Таким образом:
1
, 0 y 2, 0 x 1
f ( x, y ) 2
0, иначе.
Проверим полученный результат геометрически. Объём тела равен 1, т.е:
V h SB c SB
1
2 1
2
Следовательно, константа с рассчитана верно.
3)
Вычислим математические ожидания:
∞
∞
2
1
𝑥𝑑𝑥𝑑𝑦
= 1/2
2
−∞ −∞
0 0
∞
∞
2 1
𝑦𝑑𝑥𝑑𝑦
𝑀𝑦 = ∫ ∫ 𝑦𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ ∫
=1
2
−∞ −∞
0 0
𝑀𝑥 = ∫ ∫ 𝑥𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ ∫
4)
Вычислим дисперсии:
∞
∞
2
1
𝑥2
1
𝐷𝑥 = ∫ ∫ 𝑥 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 −
=∫ ∫
− = 1/12
4
−∞ −∞
0 0 2𝑑𝑥𝑑𝑦
∞
∞
2 1
2
𝑦
𝐷𝑥 = ∫ ∫ 𝑦 2 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 − 𝑀𝑦2 = ∫ ∫
− 1 = 1/3
−∞ −∞
0 0 2𝑑𝑥𝑑𝑦
2
𝑀𝑥2
Вычислим корреляционный момент:
2
1
𝐾𝑥𝑦 = ∫ ∫
0
5)
0
𝑥𝑦𝑑𝑥𝑑𝑦
1 1
− 𝑀𝑥 𝑀𝑦 = − ∗ 1 = 0
2
2 2
Вычислим коэффициент корреляции между величинами X и Y:
𝐾𝑥𝑦
0
𝑅𝑥𝑦 =
=
=0
√𝐷𝑥 𝐷𝑌 √1 1
2∗3
Ответ: R XY 0
12
Задача №9.1
Вычислить математическое ожидание и дисперсию величин U и V, а также определить их
коэффициент корреляции Ruv
𝑈 = 𝑎0 + 𝑎1 𝑋1 + 𝑎2 𝑋2
𝑉 = 𝑏0 + 𝑏1 𝑋2 + 𝑏2 𝑋3
A0
-9
A1
-1
A2
9
B0
2
B1
-3
B2
5
M1
1
M2
-2
M3
2
D1
1
D2
4
D3
9
K12
1
K23
3
Решение
Вычислим математические ожидания U и V
𝑚𝑢 = 𝑎0 + 𝑎1 𝑚1 + 𝑎2 𝑚2 = −28
𝑚𝑣 = 𝑏0 + 𝑏1 𝑚2 + 𝑏2 𝑚3 = 14
Вычислим дисперсии Du и Dv
𝐷𝑢 = 𝑎12 𝐷1 + 𝑎22 𝐷2 + 2𝑎1 𝑎2 𝐾12 = 307
𝐷𝑣 = 79
Рассчитаем корреляционный момент Kuv
𝐾𝑢𝑣 = 𝑀[𝑈𝑉] − 𝑚𝑢 𝑚𝑣
𝑀[𝑈𝑉] = 𝑀[(𝑎0 + 𝑎1 𝑋1 + 𝑎2 𝑋2 )(𝑏0 + 𝑏1 𝑋2 + 𝑏2 𝑋3 )]
= 𝑀[−18 + 45𝑚2 − 45𝑚3 − 2𝑚1 + 3(𝑚1 𝑚2 + 𝐾12 ) − 5(𝑚1 𝑚3 + 𝐾13 )
+ 45(𝑚2 𝑚3 + 𝐾23 ) − 27𝑚22 ] = −373.5
Таким образом
𝐾𝑢𝑣 = −373.5 + 392 = 18.5
Рассчитаем величину Ruv
𝑅𝑢𝑣 =
𝐾𝑢𝑣
√𝐷𝑢 𝐷𝑣
=
18.5
√307 ∗ 79
Ответ:Ruv = 0.11
13
= 0.11
K13
1.5
Задача №10.1
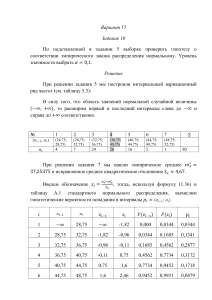
По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить график эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить точечные оценки математического ожидания и дисперсии;
- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);
- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при
помощи критерия согласия 2 и критерия Колмогорова ( = 0,05).
График гипотетической функции распределения F0(x) построить совместно с графиком F*(x) в
той же системе координат и на том же листе.
Одномерная выборка № 1:
0.19 0.97 0.59 0.01 0.94 1.10 0.23 0.86 0.38 0.13 0.53 0.92 1.07 0.12 1.32 0.20 0.13
0.35 0.38 0.58 3.35 0.94 1.27 1.98 0.22 2.25 0.73 0.03 1.18 1.06 1.12 0.41 2.73 0.99
0.84 1.15 0.14 0.36 0.53 1.10 0.04 0.84 0.18 1.32 0.29 0.17 0.29 0.93 1.13 0.04 0.08
0.23 0.01 0.04 0.38 0.11 0.72 0.31 0.47 0.59 0.17 0.50 0.02 0.07 1.11 0.62 0.97 0.08
0.69 1.51 0.26 1.26 2.06 2.50 4.13 1.13 0.16 1.15 0.18 0.15 1.33 0.26 0.42 1.14 0.37
0.96 0.84 1.14 0.02 0.87 0.13 1.07 0.27 1.60 1.01 0.91 1.46 0.81 0.19 0.80
Решение
Построим гистограмму равноинтервальным способом. Для построения гистограммы составим
интервальный статистический ряд, учитывая, что длина у всех интервалов должна быть
одинаковая.
M n 100 10 - количество интервалов
X X 1 4.13 0.01
hj n
0,412 - ширина интервала;
M
10
p*j
f
*
j
vj
n
p*j
hj
- частота попадания СВ X в j-ый интервал;
- статистическая плотность в j-ом интервале.
14
j
Aj
Bj
hj
vj
pj*
fj*
1
2
3
4
5
6
7
8
9
10
0,01
0,42
0,83
1,24
1,65
2,06
2,47
2,88
3,29
3,7
0,42
0,83
1,24
1,65
2,06
2,47
2,88
3,29
3,7
4,11
0,41
0,41
0,41
0,41
0,41
0,41
0,41
0,41
0,41
0,41
42
14
29
8
2
2
2
0
1
0
0,42
0,14
0,29
0,08
0,02
0,02
0,02
0
0,01
0
1,02439
0,341463
0,707317
0,195122
0,04878
0,04878
0,04878
0
0,02439
0
1.2
1
0.8
0.6
Series1
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
3.5
4
Построим гистограмму равновероятностным способом
Для построения гистограммы составим интервальный статистический ряд, учитывая что
частота попадания СВ X в в каждый j-ый интервал должна быть одинаковая.
15
j
Aj
Bj
hj
vj
pj*
fj*
1
2
3
4
5
6
7
8
9
10
0,01
1
0,165
0,245
0,38
0,59
0,85
0,98
1,13
1,325
1
0,165
0,245
0,38
0,59
0,85
0,98
1,13
1,325
4,13
0,99
-0,835
0,08
0,135
0,21
0,26
0,13
0,15
0,195
2,805
10
10
10
10
10
10
10
10
10
10
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,10101
-0,11976
1,25
0,740741
0,47619
0,384615
0,769231
0,666667
0,512821
0,035651
1.4
1.2
1
0.8
0.6
Series1
0.4
0.2
0
-0.2
0
0.5
1
1.5
Вычислим точечные оценки математического ожидания и дисперсии:
1 n 100
M X* xi 0,758
n i 1
2
1 n100
D X*
xi M X* 0,512
n 1 i 1
Вычислим интервальные оценки математического ожидания и дисперсии (γ = 0,95)
DX
I ( M X ) M X z
; M X z
n
z0,95 arg Ф0,475 1,96
DX
n
z arg Ф
2
0,512
0,512
I ( M X ) 0,758 1,96
; 0,758 1,96
0,618; 0,898;
100
100
16
2
2
I ( D X ) D X z
D X ; D X z
DX
n 1
n 1
2
2
0,512 1,96
0,512 ;0,512 1,96
0,512 0,369; 0,655;
99
99
По виду графика эмпирической функции распределения F * ( x) и гистограмм выдвигаем
двухальтернативную гипотезу о законе распределения случайной величины X:
H0 – величина X распределена по экспоненциальному закону:
f ( x ) f 0 ( x ) e x ;
F ( x) F0 ( x) 1 e x ;
*
1
MX
H1 – величина X не распределена по экспоненциальному закону
f ( x) f 0 ( x);
Таким
образом
получаем
F ( x) F0 ( x)
полностью
определенную
гипотетическую
функцию
распределения:
F0 ( x) 1 e
x
MX
1 e
x
0, 758
Проверим гипотезу о экспоненциальном законе по критерию Пирсона 2 . Вычислим
значение критерия 2 на основе равноинтервального статистического ряда:
10
100
2
p
j
p*j
2
pj
j 1
Теоретические вероятности попадания в интервалы вычислим по формуле:
p j F0 ( B j ) F0 ( Aj ) e
17
Bj
MX
e
Aj
MX
j
Aj
1
2
3
4
5
6
7
8
9
10
0
0,42
0,83
1,24
1,65
2,06
2,47
2,88
3,29
3,7
*
j
F0 ( A j )
F0 ( B j )
Pj
P
0,42
0,013
0,83
0,425
1,24
0,665
1,65
0,805
2,06
0,887
2,47
0,934
2,88
0,962
3,29
0,978
3,7
0,987
100
0,992
Сумма:
0,425
0,665
0,805
0,887
0,934
0,962
0,978
0,987
0,992
1,000
0,412
0,240
0,140
0,081
0,047
0,028
0,016
0,009
0,005
0,008
1,000
0,42
0,14
0,29
0,08
0,02
0,02
0,02
0
0,01
0
1,000
Bj
P
*
j
Pj
2
Pj
0,000
0,042
0,161
0,000
0,016
0,002
0,001
0,009
0,004
0,008
0,243
Проверим правильность вычислений p j :
10
1 p j 0 0,01;
j 1
Вычислим критерий Пирсона:
10
100
2
p
j
p *j
pj
j 1
2
24,3 ;
Определим число степеней свободы:
k M s 1 10 1 1 8;
Выбираем критическое значения критерия Пирсона из таблицы [1, стр.63] для степени свободы
k 8 и заданного уровня значимости 0,05 :
02,05;7 15,51
2 24,3 02,05;8 15,51
Так как условие не выполняется, то гипотеза H0 об экспоненциальном законе распределения не
принимается (однако нет оснований ее отклонить).
18
Задача №10.1
По выборке двухмерной случайной величины:
- вычислить точечную оценку коэффициента корреляции;
- вычислить интервальную оценку коэффициента корреляции 0,95 ;
- проверить гипотезу об отсутствии корреляционной зависимости 0,05 ;
- вычислить оценки параметров a0 и a1 линии регрессии y a0 a1x ;
- построить диаграмму рассеивания и линию регрессии.
Двумерная выборка №1:
(-11.03;-10.74) (2.22; -8.72) (-5.28; -2.96) ( -1.86; -6.39) ( -2.81; 1.61) ( -6.39;-5.63) ( -3.04; -7.92)
( -1.26; -5.98) (-5.87; -3.86) (-2.84; -3.45) ( -3.75; -3.31) ( -9.25; -8.91) (-8.59; -5.81) ( -2.49; -3.04)
( -5.64;-11.00) ( -3.84; -7.75) (-4.12; -3.56) (-5.90; -5.63) (-2.46; -7.49) ( -0.06; -3.62) ( -4.70; -9.40)
(2.57; -1.16) ( -7.37; -5.09) (-3.20; -3.43) (-7.20; -2.45) ( -0.73; -1.98) ( -5.99; -5.66) ( -2.76; -4.16)
(-5.45; -2.52) (-9.00; -1.30) ( -0.10; -8.55) ( -6.24; -2.06) (-2.94; -4.68) (-1.54; -2.33) (-1.44; -9.95)
(0.63; -6.17) (-4.71; 1.64) (-10.73; -1.48) (-4.44;-12.69) (-3.44; -7.23)(-1.23; -4.27) (-1.03; -7.81)
(-7.06; -3.94) ( -5.22;-10.72) (-3.12; -8.23) (-3.23;-3.23) (-8.29; -5.97) (-0.35; -6.60) (-4.65; -2.56)
(-2.92; -2.09)
Решение
Для удобства все промежуточные вычисления поместим в таблицу, вычислим:
Оценки математических ожиданий по каждой переменной:
1 n
m xi 4
n i 1
*
X
1 n
m y i -5,2
n i 1
*
Y
Оценки начальных моментов второго порядка по каждой переменной:
2* ( x)
1 n 2
xi 25,279
n i 1
2* ( y )
1 n 2
yi 37,222
n i 1
Оценку смешанного начального момента второго порядка:
1 n
xi yi 20,924
n i 1
Оценки дисперсий:
1*,1 ( x, y )
D X*
n
n
2* ( x)
m X2 9,467
n 1
n 1
DY*
Оценку корреляционного момента:
*
K XY
n
n
1*,1 ( x, y )
m *X mY* 0,127
n 1
n 1
19
n
n
2* ( y )
mY2 10,39
n 1
n 1
Результаты промежуточных вычислений
x
y
x2
y2
x*y
-11,03
2,22
-5,28
-1,86
-2,81
-6,39
-3,04
-1,26
-5,87
-2,84
-3,75
-9,25
-8,59
-2,49
-5,64
-3,84
-4,12
-5,9
-2,46
-0,06
-4,7
2,57
-7,37
-3,2
-7,2
-0,73
-5,99
-2,76
-5,45
-9
-0,1
-6,24
-2,94
-1,54
-1,44
0,63
-4,71
-10,73
-4,44
-3,44
-1,23
-1,03
-7,06
-10,74
-8,72
-2,96
-6,39
1,61
-5,63
-7,92
-5,98
-3,86
-3,45
-3,31
-8,91
-5,81
-3,04
-11
-7,75
-3,56
-5,63
-7,49
-3,62
-9,4
-1,16
-5,09
-3,43
-2,45
-1,98
-5,66
-4,16
-2,52
-1,3
-8,55
-2,06
-4,68
-2,33
-9,95
-6,17
1,64
-1,48
-12,69
-7,23
-4,27
-7,81
-3,94
121,661
4,928
27,878
3,460
7,896
40,832
9,242
1,588
34,457
8,066
14,063
85,563
73,788
6,200
31,810
14,746
16,974
34,810
6,052
0,004
22,090
6,605
54,317
10,240
51,840
0,533
35,880
7,618
29,703
81,000
0,010
38,938
8,644
2,372
2,074
0,397
22,184
115,133
19,714
11,834
1,513
1,061
49,844
115,348
76,038
8,762
40,832
2,592
31,697
62,726
35,760
14,900
11,903
10,956
79,388
33,756
9,242
121,000
60,063
12,674
31,697
56,100
13,104
88,360
1,346
25,908
11,765
6,003
3,920
32,036
17,306
6,350
1,690
73,103
4,244
21,902
5,429
99,003
38,069
2,690
2,190
161,036
52,273
18,233
60,996
15,524
118,462
-19,358
15,629
11,885
-4,524
35,976
24,077
7,535
22,658
9,798
12,413
82,418
49,908
7,570
62,040
29,760
14,667
33,217
18,425
0,217
44,180
-2,981
37,513
10,976
17,640
1,445
33,903
11,482
13,734
11,700
0,855
12,854
13,759
3,588
14,328
-3,887
-7,724
15,880
56,344
24,871
5,252
8,044
27,816
20
-5,22
-3,12
-3,23
-8,29
-0,35
-4,65
-2,92
-11,03
2,22
Сумма: -200,14
-10,72
-8,23
-3,23
-5,97
-6,6
-2,56
-2,09
-10,74
-8,72
-260,23
27,248
9,734
10,433
68,724
0,123
121,661
4,928
27,878
3,460
1263,9
114,918
67,733
10,433
35,641
43,560
6,554
4,368
115,348
76,038
1861,1
55,958
25,678
10,433
49,491
2,310
11,904
6,103
118,462
-19,358
1046,2
Точечную оценку коэффициента корреляции:
R
*
XY
*
K XY
D X DY
1
50
∗ 1263,9 −
∗ 16 = 9,44
49
49
1
50
𝐷𝑥 =
∗ 1861,1 −
∗ 27,04 = 10.39
49
49
1
50
𝐾𝑥𝑦 =
∗ 1046,2 −
∗ (−4)(−5,2) = 0,13
49
49
𝐷𝑥 =
𝑅𝑥𝑦 =
0,13
√98
= 0,01
Вычислим интервальную оценку коэффициента корреляции с заданной надёжностью 0,95 ,
По таблице функции Лапласа [1, стр, 61] z0,95 arg Ф(0,475) 1,96 :
*
1 R XY
a 0,5 ln
*
1 R XY
z
0,01 - 0,28 0,27
n3
*
z
1 R XY
b 0,5 ln
0,01 0,28 0,29
*
n3
1 R XY
Таким образом, доверительный интервал для коэффициента корреляции имеет вид:
I ( R XY ) 0,27;0,29
Проверим гипотезу о корреляционной зависимости:
H 0 : RXY 0;
H1 : RXY 0.
21
Так как объём выборки велик (n>50), то критерий вычислим по формуле:
Z
R * XY n
1 R * XY
2
0,07 / 0,99 0.07
1 0,05
По таблицы функции Лапласа Z 0, 05 arg Ф
1,96 ,
2
Так как Z Z , то гипотеза H 0 принимается, т,е, величины X и Y не коррелированны
Вычислим оценки параметров линии регрессии:
1*
*
K XY
0,01
DX
0* mY* 1* m *X 0,53
22