Тема. Практическая работа. Решение экспериментальных задач.
реклама

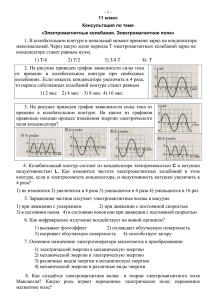
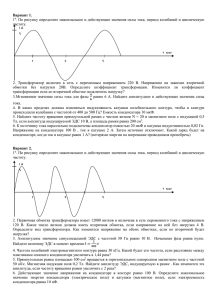
Тема. Практическая работа. Решение экспериментальных задач. Цели урока: Образовательные: проверить усвоение физических формул и умений брать первую и вторую производную от тригонометрических функций, формировать умения решать расчетные и качественные задачи, анализировать графики и физические закономерности. Развивающие: развивать творческое мышление, развивать умение применять знания в новой нестандартной ситуации, развивать умение анализировать, делать выводы. Воспитательные: воспитывать доброжелательное отношение друг к другу, взаимопонимание и взаимопомощь. Задачи: выявить связи, существующие между физикой и математикой, показать, что на основе производной возможен анализ конкретных физических ситуаций. Ход урока. 1.Оргмомент 2. Повторение пройденного материала физических ситуаций 1 вариант № 1. Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени t по закону . Записать закон зависимости силы тока от времени i(t). Найти период и частоту колебаний в контуре, амплитуду колебаний заряда и амплитуду колебаний силы тока i(t). №2. Конденсатор емкостью 0,5 мкФ включен в сеть переменного тока. Определить период колебаний переменного тока, если емкостное сопротивление конденсатора равно 20 Ом. №3. При включении конденсатора сила тока в цепи переменного тока с частотой 50 Гц и напряжением 220 В равна 0,14 А. Определите емкость конденсатора. Активным сопротивлением цепи можно пренебречь. №4В сеть переменного тока с частотой 50 Гц и напряжением 220 В включена катушка с индуктивностью 60 мГн и ничтожно малым активным сопротивлением. Найдите действующее и амплитудное значение силы тока в цепи катушки. №5Если зависимость силы тока от времени в колебательном контуре выражается уравнением i = 10-4 cos(ωt + ), то при силе тока в цепи 10-4А 2 энергия А) в конденсаторе максимальная, в катушке – равна 0. В) в конденсаторе и в катушке распределена поровну. С) в конденсаторе увеличивается, в катушке уменьшается. Д) в конденсаторе уменьшается, в катушке увеличивается. 2 вариант №1.В колебательном контуре совершаются незатухающие электромагнитные колебания. Определить силу тока в контуре при t = 0,002 с от начала отсчета, если заряд конденсатора изменяется по гармоническому закону: №2.В колебательном контуре происходят незатухающие электромагнитные колебания. Определить максимальную силу тока в контуре, если емкость конденсатора С = 210-5 Ф, индуктивность катушки L = 5 Гн и заряд конденсатора меняется по закону . №3. Катушка индуктивностью 15 мГн включена в сеть промышленного переменного тока. Определить ее индуктивное сопротивление. №4.Конденсатор емкостью 24 мкФ и катушка индуктивностью 0,05 Гн с активным сопротивлением 100 Ом подключены последовательно к источнику переменного тока, в котором напряжение на зажимах равно 120 В при частоте 50 Гц. Определить действующие значения силы тока в цепи напряжения на конденсаторе и катушке №5 Катушка при частоте тока 2 кГц обладает индуктивным сопротивление 157 Ом. Индуктивность этой катушки равна А) 3,14 Гн В) 12,5 мГн. С) 6,28 · 10-4Гн. -2 Д) 0,785 Гн. Е) 2 · 10 Гн №6 Если зависимость силы тока от времени в колебательном контуре выражается уравнением Е) в конденсаторе равна 0, в катушке – максимальная. №6 Сила тока через катушку колебательного контура изменяется по закону i = 0,4sin106t. Емкость конденсатора контура 200 пФ, значит индуктивность катушки равна А) 4 м Гн В) 2·10-4 Гн С) 0,8·102 Гн Д) 5 м Гн Е) 0,2 Гн №7 Из уравнения определить действующее значение силы тока i = 20cos(ωt + ), 2 g = 10-6 cos(ωt + ), то при заряде в цепи 10-6Кл энергия 3 А) в конденсаторе максимальная, в катушке – равна 0. В) в конденсаторе и в катушке распределена поровну. С) в конденсаторе увеличивается, в катушке уменьшается. Д) в конденсаторе уменьшается, в катушке увеличивается Е) в конденсаторе равна 0, в катушке – максимальная. №7 Из уравнения определить действующее значение напряжения u = 10cos(ωt + ), 2