Лабораторная работа №1. «Изучение теории расчёта

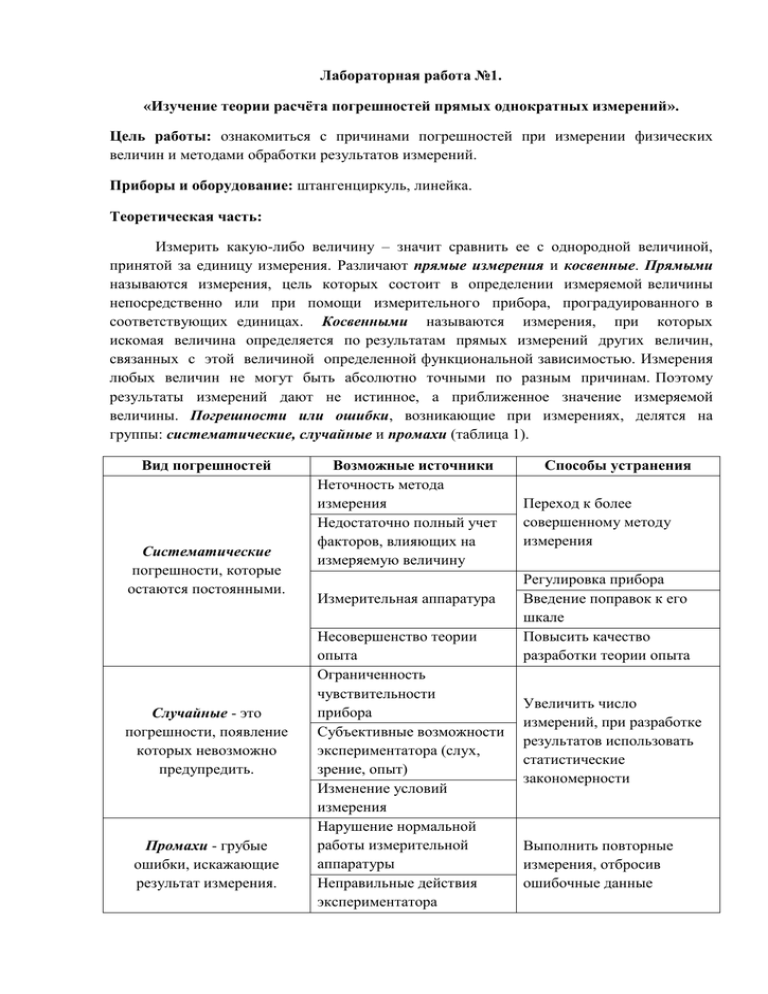
Лабораторная работа №1.
«Изучение теории расчёта погрешностей прямых однократных измерений».
Цель работы: ознакомиться с причинами погрешностей при измерении физических
величин и методами обработки результатов измерений.
Приборы и оборудование: штангенциркуль, линейка.
Теоретическая часть:
Измерить какую-либо величину – значит сравнить ее с однородной величиной,
принятой за единицу измерения. Различают прямые измерения и косвенные. Прямыми
называются измерения, цель которых состоит в определении измеряемой величины
непосредственно или при помощи измерительного прибора, проградуированного в
соответствующих единицах. Косвенными называются измерения, при которых
искомая величина определяется по результатам прямых измерений других величин,
связанных с этой величиной определенной функциональной зависимостью. Измерения
любых величин не могут быть абсолютно точными по разным причинам. Поэтому
результаты измерений дают не истинное, а приближенное значение измеряемой
величины. Погрешности или ошибки, возникающие при измерениях, делятся на
группы: систематические, случайные и промахи (таблица 1).
Вид погрешностей
Систематические
погрешности, которые
остаются постоянными.
Случайные - это
погрешности, появление
которых невозможно
предупредить.
Промахи - грубые
ошибки, искажающие
результат измерения.
Возможные источники
Неточность метода
измерения
Недостаточно полный учет
факторов, влияющих на
измеряемую величину
Измерительная аппаратура
Несовершенство теории
опыта
Ограниченность
чувствительности
прибора
Субъективные возможности
экспериментатора (слух,
зрение, опыт)
Изменение условий
измерения
Нарушение нормальной
работы измерительной
аппаратуры
Неправильные действия
экспериментатора
Способы устранения
Переход к более
совершенному методу
измерения
Регулировка прибора
Введение поправок к его
шкале
Повысить качество
разработки теории опыта
Увеличить число
измерений, при разработке
результатов использовать
статистические
закономерности
Выполнить повторные
измерения, отбросив
ошибочные данные
В зависимости от того, с какой точностью требуется произвести измерения,
используют технические или лабораторные методы.
Прямые однократные измерения и их погрешности
При использовании технических методов надо произвести одно измерение. В этом
случае точность измерения определяется погрешностью прибора и погрешностью отсчёта.
Результатом измерения служит запись в виде: N=No ± ∆N, где: No – отсчет по прибору; ∆N
– абсолютная погрешность измерения. Абсолютная погрешность прямого технического
измерения при несовпадении указателя со штрихом шкалы равна сумме абсолютной
погрешности прибора, которая определяется исходя из класса точности прибора и
границы погрешности отсчёта, т.е.:
∆𝑁 = ∆прибора + ∆отсчёта
Класс точности
прибора характеризует
(1)
приведенная погрешность
прибора
εПР,
которая равна отношению абсолютной ∆прибора погрешности прибора к предельному
значению NПР измеряемой величины (т. е. к ее максимальному значению по шкале
прибора), выраженному в процентах:
𝜀ПР =
Приведенная
погрешность
∆прибора
𝑁ПР
∙ 100%
прибора
является
(2)
по
существу
относительной
погрешностью. По приведенной погрешности приборы делятся на:
1) технические - класса точности 1; 1,5; 2,5; 4;
2) лабораторные - класса точности 0,1; 0,2; 0,5.
Класс точности прибора указан на шкале прибора. Абсолютная погрешность, которую
дает прибор, определяется из выражения (2):
𝜀
ПР
∆прибора = 100%
∙ 𝑁ПР
(3)
где: εПР - класс точности прибора; NПР - предельное значение измеряемой величины по
шкале прибора.
Если на шкале класс точности не обозначен, то абсолютная погрешность
прибора принимается равной половине цены деления наименьшего значения шкалы
прибора.
Погрешности приборов не зависят от числа измерений, они зависят от конструкции
прибора. Для более точных измерений либо подбирают приборы более высокого
класса точности, либо используют лабораторные методы измерений.
Основные правила оценки границы абсолютной погрешности при проведении
прямых измерений:
1. Определить основную погрешность прибора и выразить ее через цену деления
шкалы прибора.
2. Сравнить основную погрешность прибора ∆прибора с наибольшим значением
с
погрешности отсчёта ∆отсчёта = 2.
1
с
Если выполняется условие ∆прибора < 4 ∙ 2, то
общая граница абсолютной погрешности равна погрешности отсчёта: ∆𝑁 =
с
∆отсчёта = 2.
3. Если выполняется условие ∆прибора > 2с, то можно считать общую границу
абсолютной погрешности равной основной погрешности прибора: ∆𝑁 = ∆прибора .
4. Если соотношение между ценой деления и погрешностью прибора не подчиняется
условиям 2 или 3, то можно считать, что общая граница погрешности равна:
∆𝑁 = ∆прибора + ∆отсчёта
5. Сложение границы погрешности отсчёта с погрешностью прибора, два слагаемых в
формуле для оценки границ погрешности результата измерений цифровым
прибором иллюстрирует общий фундаментальный принцип теории погрешностей:
если процесс измерения некоторой величины сопровождается погрешностями
разного вида d1, d2, d3, …, dn, то погрешность результата d определяется суммой
частных погрешностей в соответствии с квадратичным законом сложения:
𝑑 = √𝑑12 + 𝑑22 + 𝑑32 + ⋯ + 𝑑𝑛2
6.
В общем виде можно записать выражение для расчёта абсолютной погрешности:
∆𝑁 = √∆2прибора + ∆2отсчёта
Задание №1.
Цель: отработка навыков прямых однократных измерений и расчёта их погрешностей.
Задача: изучение штангенциркуля, линейки для технического метода измерения
линейных величин.
Штангенциркуль (от нем. Stangenzirkel) -
универсальный
инструмент,
предназначенный для высокоточных измерений наружных и внутренних размеров, а
также глубин отверстий. Штангенциркуль — один из самых распространенных
инструментов измерения благодаря простой конструкции, удобству в обращении и
быстроте в работе.
Устройство штангенциркуля:
1. штанга;
2. подвижная рамка;
3. шкала штанги;
4. губки для внутренних измерений;
5. губки для наружных измерений;
6. линейка глубиномера;
7. нониус – шкала на подвижной рамке;
8. винт для зажима рамки.
Порядок определения размера следующий:
1. Первая («нулевая») насечка нониуса отсекает на линейке количество целых
миллиметров.
2. На
фотографии
«нулевая»
отметка
нониуса
находится
правее
1,5
см.
Следовательно, размер объекта от 15 до 16 мм. Теперь определяем размер с
точностью до десятых долей миллиметра, для этого:

находим на штангенциркуле класс точности прибора; для данного
штангенциркуля он составляет 0,1 мм;

смотрим, какая насечка нониуса совпадает со шкалой линейки (на фото это
седьмая насечка);

умножив номер насечки на класс точности прибора получим десятые доли
миллиметра: 7 · 0,1 = 0,7 мм;

складывая целую часть с дробной получаем истинный размер: 15 + 0,7 =
15,7 мм;

абсолютную погрешность, которую даёт прибор, рассчитываем по формуле
(2):
𝜀
ПР
∆прибора = 100%
∙ 𝑁ПР или ∆прибора =
0,145 мм;
(класс точности)∙(верхний предел)
100
=
0,1 мм∙145
100
=

граница погрешности отсчёта определяется половиной цены деления, т.е.
∆отсчёта =

0,1 мм
2
= 0,05 мм;
проверить пункты 2,3,4 основных правил оценки границы абсолютной
погрешности при проведении прямых измерений;

т.к. выполняется пункт 3, то ∆𝑁 = ∆прибора = 0,145 мм;

результат записываем в виде: N=No ± ∆N, N=(15,7±0,145) мм, но т.к. границу
абсолютной погрешности необходимо округлить до одной значащей цифры,
то окончательный результат имеет вид: N=(15,7±0,1) мм.
Тренировочное задание №1.
Используя фотографию, определить диаметр металлического шарика и записать результат
измерения с учётом погрешности прибора.
Тренировочное задание №2.
Используя линейку, класс точности которой не указан, определить длину карандаша
или ручки и записать результат измерения с учётом погрешности прибора.