4-й семинар, гидростатика, относ.равноесие при плоско

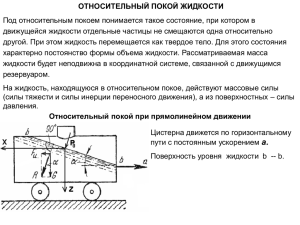
1
4-й семинар, 2016г.
4. «Гидростатика. Равновесие жидкости в движущихся сосудах»
При относительном покое жидкость движется вместе с сосудом. Это состояние
относительного равновесия. Равновесие частицы жидкости при движении можно
рассматривать, если воспользоваться принципом Даламбера и приложить к частице силы
инерции.
Дифференциал давления
dp = ρ( Xdx + Ydy + Zdz),
(1)
где ρ - плотность жидкости; X, Y,Z –сумма проекций ускорений массовых сил
(тяжести и инерции переносного движения) или суммы проекции единичных массовых
сил на соответствующие оси координат.
Вдоль поверхности равного давления дифференциал равен нулю dp = 0, поэтому
дифференциальное уравнение любых поверхностей уровня, в том числе свободной
поверхности
Xdx +Ydy + Zdz =0.
(2)
Поверхности уровня - поверхности равного давления в каждой точке нормальны
направлению вектора единичной массовой силы, действующей в этой точке.
При движении объема жидкости в сосуде на него действуют:
- поле сил тяжести: единичная массовая сила – g, ускорение свободного падения;
- поле сил в относительном движении – а, ускорение переносного движения.
Рассмотрим условие равновесия частицы жидкости с координатами х0, z0 под
действием массовых и поверхностных сил при движении под углом вверх в проекциях на
оси, связанные с движущимся сосудом, при этом ось Х и У в горизонтальной плоскости, а
Z перпендикулярна горизонтальной плоскости. Выбор осей важен, так как при выводе
уравнения получаем функцию, которая отражает изменение положения поверхности.
Единичные массовые силы это ускорения. Cпроектируем их на оси координат Z,
X, расположенные так как показано на рис.1.
4.1. Определение давления в любой точке при прямолинейном движении.
Проекции единичных массовых сил на оси (рис.1)
Ox: X =- jCosα=-aCosα,
Oz : Z =-( jSinα+g)=-(αSina+g),
Оу: Y = 0.
Давление в любой точке жидкости, находящейся в относительном покое при
прямолинейном равноускоренном движении
Р = P0+ρ(aCosα)*(x0-х)+ρ(aSinα + g)*(z0 – z). (3)
2
Рис.4.1 Силы, действующие на жидкость при прямолинейном движении по
плоскости с ускорением а; а) движение сосуда с ускорением вверх, б) план ускорений. α –
угол наклона плоскости,β – угол поворота свободной поверхности, g-ускорение
свободного падения, j-ускорение силы инерции, q – суммарное ускорение, В,Н – ширина
сосуда, высота жидкости в сосуде при горизонтальном его положении, Z,Х – проекции
суммарного ускорения на оси Z и X, связанные с сосудом.
4.2. Определение положения поверхностей равного давления при
прямолинейном движении
На произвольной поверхности равного давления постоянно Р → const, поэтому
дифференциал давления dp=0.
Уравнение свободной поверхности
 aCos  * ( x0  х)   aSin
z0  z  
 g  *  z0 – z   0.
aCos
*( x0  x)  tg  ( x0  x),
aSin  g
tg   
(4)
aCos
.
aSin  g
Это уравнение прямой линии, как проекции свободной поверхности на
вертикальную плоскость, β – угол наклона этой линии к оси Х, коэффициент в уравнении
поверхности равен тангенсу угла β - угол наклона пьезометрической поверхности к оси Х.
Для определения положения свободной поверхности жидкости в сосуде,
движущемся прямолинейно и равноускорено, к уравнению (4) нужно добавить
уравнение объемов, т. е. нужно знать первоначальный объем жидкости в сосуде и
выразить его через размеры сосуда В и уровень Н жидкости в нем. Используя
величины В и Н найдем Хо, Уо.
3
Если сосуд движется с постоянным ускорением по горизонтальной плоскости α=0,
j= -а, tgβ=а/g, свободная поверхность наклоняется на угол β (рис. 2а).
Если сосуд движется по наклонной плоскости под действием силы тяжести) j=
gSinα, tgβ=tgα, свободная поверхность параллельна горизонтальной плоскости (рис. 2б).
Движущей силой является сила тяжести, проекция ускорения силы тяжести на
наклонную плоскость a   g * Sin . Рассматривая равновесие сил по правилу Даламбера
прикладываем к точке единичную силу j  a  g * Sin , проектируем на оси координат
связанные с сосудом ускорения:
Z   g  g * Sin 2 , X  g * Sin * Cos ,
X
g * Sin * Cos
tg     
 tg .
Z
 g  g * Sin 2
При условии, что трение при движении отсутствует.
Если сосуд движется с ускорением а вниз вертикально j=-a, q=a-g, α = 270°, (рис.
2в).
4. Если сосуд движется с ускорением а вверх вертикально, j=-a, q=a+g, α = 90°
(рис.2г).
Рис. 2.Движение сосуда по наклонной плоскости по горизонтальной плоскости (а) под
действием собственного веса (б), вниз с ускорением(в), вверх с ускорением(г).
Для определения давления в любой точке можно также использовать суммарное
ускорение q (суммарную массовую единичную силу ).
Возьмем на рис.4.1 около точки М площадку dS, параллельную свободной
поверхности и на этой площадке построим цилиндрический объем с осью, нормальной к
свободной поверхности. Условие равновесия указанного объема жидкости в направлении
нормали к свободной поверхности будет иметь вид
РdS = P0dS + q(ρlMdS),
4
где последний член представляет собой полную массовую силу, q – суммарная
единичная массовая сила, М = ρlMdS - масса выделенного объема жидкости, l —
расстояние от точки М до свободной поверхности. После сокращения на dS получим
давление в точке
Р = P0 + qρlM,
(5)
4.3. Определение сил давления на стенки.
Силы давления жидкости на стенки при относительном равновесии определяются
также как при равновесии жидкости в неподвижном сосуде. Нужно иметь в виду: какие
ускорения при определении давления используются. На рис. 3. показан сосуд,
движущийся в направлении, указанном стрелкой ускорения а, cуммарное ускорение
q=a+g. Над свободной поверхностью имеется избыточное давление (Ро-Ратм)=М,
поэтому П.П. поднимается относительно свободной поверхности на величину h0u 
M
.
g
Рис. 3. Определение сил, действующих на стенки, при прямолинейном движении
сосуда с жидкостью. 1) ускорение инерции j=-а; 2)положение П.П.-h0u(h0uq); 3)
положение ц.т. относительно свободной поверхности – h1(h1q); 4) положение ц.т.
относительно П.П.;5) α- угол между горизонталью и ускорением а; β – угол наклона
поверхностей равного давления относительно горизонтали; γ – угол наклона площадки
относительно горизонтали. Индекс q относится к суммарному ускорению.
Давление в ц.т. площадки будет определяться по известным формулам. Например,
при использовании пьезометрической высоты
hCq= h1q+h0q,
5
Рс=ρ*q* hCq, (6)
где hCq= hc*Cosβ – пьезометрическая высота при относительном покое П.П. , h1q=
h1*Cosβ – расстояние от ц.т. до П.П., h0uq=h0u*Cosβ – подьем П.П. относительно
свободной поверхности при относительном покое.
Сила давления, воспринимаемая плоской стенкой, на несмоченной стороне
которой давление равно атмосферному
F =РС*S ,
(7)
где PС - избыточное давление в центре тяжести стенки, определяемое по формулам
(5) или (6) через расстояние hC или hСq от центра тяжести стенки до пьезометрической
плоскости; S - площадь стенки.
Сила F нормальна к стенке и проходит через центр давления D, положение
которого для данной стенки зависит от величины и направления вектора а переносного
ускорения, потому что положение пьезометрической плоскости h0и зависит от ускорения
а.
Сила давления жидкости, на криволинейную стенку вычисляется суммированием
составляющих по координатным осям. Составляющая силы давления по заданному
направлению s (рис. 4.3, а)
Рs = ρqsVs ,
(8)
Рис.4.
где qs - проекция вектора единичной массовой силы на направление s; Vs - объем
тела давления, построенного параллельно направлению s между поверхностью стенки и
пьезометрической плоскостью.
Линия действия силы Рs проходит через центр тяжести жидкости объемом Vs.
Силу давления Р жидкости на криволинейную стенку можно определить также из
условий относительного равновесия объема жидкости V, заключенного между
криволинейной стенкой и плоским сечением, проведенным через граничный контур
стенки (рис. 4.3, б):
6
Р  N G  J  N Q
(9)
где N - сила давления на плоское сечение АСВ, проведенное через граничный
контур стенки, вычисляемая по формуле (4.10); G - вес объема V жидкости (G = ρgV), Jсила инерции жидкости, заключенной в объеме V (J = ρаV); Q - суммарная массовая сила,
Q  G  J   gV   aV  V ( g   a ).
Сила давления жидкости на погруженное в нее твердое тело (рис. 4.4) складывается
из вертикальной силы Рв = ρgV, обусловленной изменением давления в жидкости под
действием силы тяжести, и силы Ри = ρаV, которая создается изменением давления в
жидкости, вызываемым переносной силой инерции. Последняя сила направлена вдоль
вектора а переносного ускорения.
Результирующая сила Р = Рв + Ри проходит через центр тяжести вытесненного
телом объема V жидкости и направлена в сторону, противоположную вектору q
единичной массовой силы.
Рис.5.