Численный пример сопровождающий лекцию
реклама

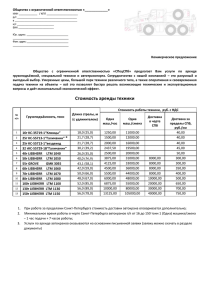
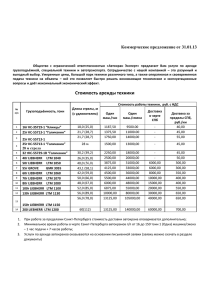
Численный пример сопровождающий лекцию – Код для программы R Этот пример также описан в книге Bartholomew, D., Steel, F., Moustaki, I. and Galbraith, J. (2002) The Analysis and Interpretation of Multivariate Data for Social Scientists. London: Chapman and Hall. Сельские жительницы (N = 8445)из Бангладеш (Huq & Cleland, 1990) заполнили короткий опросник, измеряющий социальную мобильность и свободу. Женщин спросили, могут ли они выполнить следующие действия самостоятельно (ДА или НЕТ): 1. Сходить в любую часть деревни/села / города. 2. Выйти за пределы деревни/села / города. 3. Поговорить с незнакомым мужчиной. 4. Сходить в кино / посетить культурное мероприятие. 5. Пройтись по магазинам. 6. Сходить в кооператив / клуб / клуб матерей. 7. Принять участие в политическом собрании. 8. Сходить в поликлинику / больницу. Данные включены в пакет “ltm” (аббревиатура «latent trait modelling»)статистической программы R. Полное руководство к этому пакету может быть загружено по ссылке https://duckduckgo.com/?q=ltm+package&t=ffsb Инструкции Начните с инсталляции пакета ltm из меню Packages Install package(s)…. Потом загрузите пакет в рабочую память R следующей командой: library(ltm) Теперь посмотрите как выглядят первые несколько строк массива данных Mobility: head(Mobility) Вы должны увидеть следующее: Item 1 Item 2 Item 3 Item 4 Item 5 Item 6 Item 7 Item 1 1 1 1 1 0 0 0 2 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 Это ответы на 8 вопросов первых шести женщин в выборке. 8 0 0 0 0 0 0 Теперь мы готовы к обсчету параметров. Подходящая модель – это логистическая модель с 2мя параметрами (2PL). Функция «ltm» применяет именно эту модель к нашему массиву данных (Mobility), и записывает результаты в новый объект model2PL: model2PL <- ltm(Mobility ~ z1) Параметр «z1» уточняет, что наша модель подразумевает только одно латентное качество (которое будет обозначаться z). Вызовите новый объект model2PL чтобы посмотреть результаты обсчета модели: model2PL Вы должны увидеть дискриминативность и сложность каждого пункта. Теперь нарисуйте характеристические кривые для всех пунктов: plot (model2PL, type = "ICC") А теперь подсчитайте баллы по мобильности используя метод максимального правдоподобия с а-приори нормальным распределением (метод «эмпирический Байес» или “EB”): MobilityIRT <- factor.scores(model2PL, method="EB", resp.patterns = Mobility) Баллы будут сохранены в новом объекте MobilityIRT. Этот объект содержит слишком много строк и не может быть показан целиком. Чтобы посмотреть что содержится в этом объекте, вызовите полный список его компонент: ls(MobilityIRT) Вы увидите следующие компоненты: [1] "B" "call" "coef" "method" "resp.pats" "score.dat" Из этого списка, нас интересуют непосредственно подсчитанные баллы (score.dat). Список баллов также очень длинный (8445 человек), поэтому посмотрите только первые 30 человек: MobilityIRT$score.dat[1:30,] Столбец “z1” содержит оцененный балл IRT на z шкале (тета). Столбец “se.z1” содержит стандартную ошибку измерения этого балла. Постройте график на котором для каждой испытуемой из выборки ее балл (ось X) показан с соответствующей ошибкой измерения (ось Y). plot(MobilityIRT$score.dat$z1, MobilityIRT$score.dat$se.z1) Для сравнения, также давайте подсчитаем классические баллы суммированием всех пунктов: MobilitySum<-rowSums(Mobility) Имея два разных набора баллов, постройте график соответствия между IRT и классическими баллами: plot(MobilityIRT$score.dat$z1, MobilitySum)