Долгушин А. Н. «Практикум решения физических задач

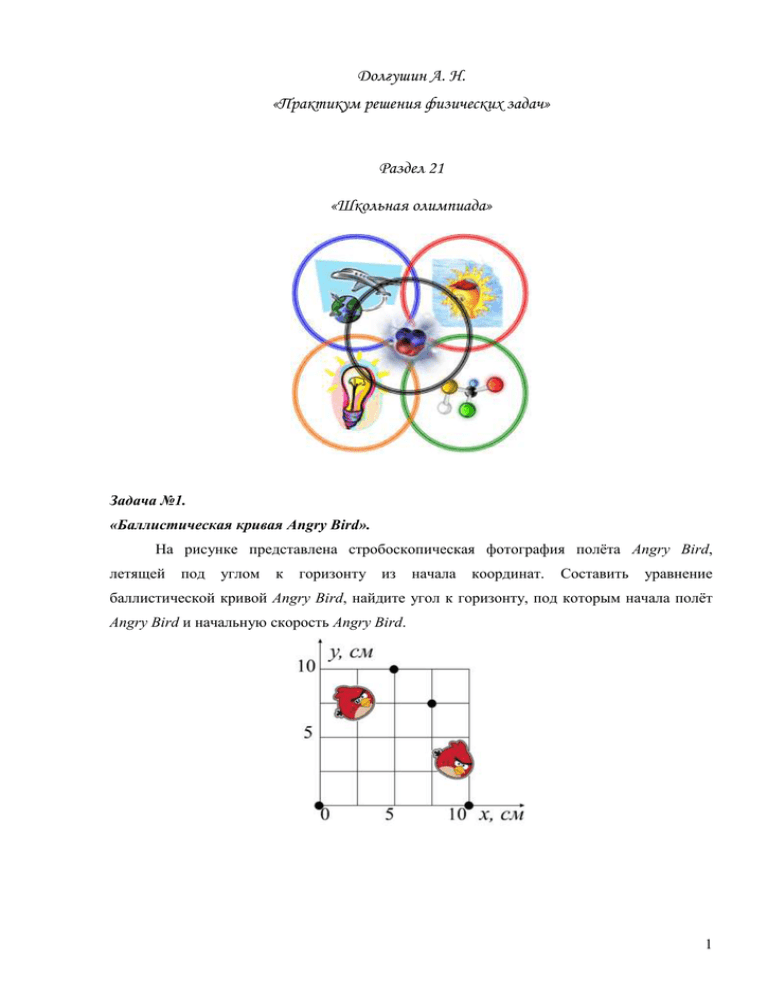
Долгушин А. Н.
«Практикум решения физических задач»
Раздел 21
«Школьная олимпиада»
Задача №1.
«Баллистическая кривая Angry Bird».
На рисунке представлена стробоскопическая фотография полёта Angry Bird,
летящей
под
углом
к
горизонту из
начала
координат.
Составить
уравнение
баллистической кривой Angry Bird, найдите угол к горизонту, под которым начала полёт
Angry Bird и начальную скорость Angry Bird.
1
Задача №2.
«На конференции физиков-теоретиков».
На научно-практической конференции физиков-теоретиков сразу два учёных
выступили с докладами, сообщавшими, что им удалось получить простые формулы,
позволяющие рассчитать силу всемирного тяготения между геометрически правильными
однородными телами, расположенными на небольшом расстоянии друг от друга. Первый
докладчик рассматривал взаимодействие между кубическими телами. По его расчётам
получалось, что силу следует вычислять по формуле F  G
m1m2 m1l1  m2 l 2 
R3
, где l1 и l2
– соответствующие стороны кубов, а R – расстояние между центрами кубов. Второй
докладчик вывел формулу для расчёта силы взаимодействия между однородными

 

m1 R 2  l12 m2 R 2  l 22
тетраэдрами (правильными треугольными пирамидами): F  G
, где
R6
l1 и l2 – соответствующие стороны треугольников, а R – расстояние между центрами
тетраэдров. Чьи расчёты можно признать ошибочными, не прибегая к подробной проверке
математических выкладок?
Решение
Проверка размерности формулы первого докладчика
F   G
m1 m2 m1 l1   m2 l2  Н  м 2 кг  кг  м


Н.
кг 2
м3
R3
Проверка размерности формулы второго докладчика
2
2
2
2
2
2
2
F   G  m1  R  l 1 m6 2  R  l 2   Н  м2  кг  м  6кг  м
кг
м
R
Н.
2
С точки зрения размерности представленные формулы обоих докладчиков верны.
Согласно принципу соответствия, любая новая теория, претендующая на более точное
описание физической реальности, чем старая, должна включать последнюю как
предельный случай. Если удалить кубы или тетраэдры на значительное расстояние (когда
l1<<R и l2<<R), их можно рассматривать как материальные точки и силу взаимодействия
между ними рассчитывать, используя закон всемирного тяготения в форме F  G
m1m2
.
R2
Эту формулу можно получить только из формулы второго докладчика, но нельзя
получить из формулы первого. Т.е. на значительном расстоянии между объектами, когда
l1<<R и l2<<R, то l1  0 , l12  0 и l 2  0 , l 22  0 . Следовательно, выводы первого
докладчика можно сразу признать ошибочными, а расчёты второго требуют более
подробного анализа.
Задача №3.
«Глубинные подводные взрывы».
Используя метод размерностей физических величин, оценить период колебаний
объема газового пузыря, образовавшегося в результате глубинного подводного взрыва.
Считать, что величина периода зависит от давления, плотности воды и полной энергии
взрыва.
Вид с палубы американского корабля береговой охраны «Спенсер» (USA Spencer) на
взрыв глубинных бомб, сброшенных с целью потопления немецкой подводной лодки U175. Время съёмки: 17 апреля 1943 г. Автор съёмки: Джек Дженьюэри. После этих
взрывов лодка всплыла, стала лёгкой мишенью корабельной артиллерии1.
1
http://great-victory.ru/?m=5327
3
Решение
С учетом условия задачи полагаем, что T ~ p a  b E c . Переходим к размерности
a
b
м
 Н   кг 
с
физических величин с ~  2   3  Н  м  . Т.к. Н  кг  2 , то после преобразований
с
м  м 
1
получаем с 1 ~ кг a b c м  a 3b  2c c 2 a 2c  кг 0 м 0 c1 ~ кг a b c м  a 3b  2c c 2 a 2c . Получаем систему
5
уравнений 0=a+b+c, 0=-a-3b+2c, 1=-2a-2c. Решением являются выражения a   ,
6
b
1
1
, c  . Найденные значения показателей подставляем в выражение для периода
2
3
колебаний объема газового пузыря T ~ p a  b E c , получаем T ~
 3 E
6
p5
.
Задача №4.
«Рождение новой звезды».
В межзвездной среде с плотностью  вспыхнула новая звезда. Её оболочка
расширяется. В момент вспышки масса оболочки равна М0. Определить радиус оболочки
к тому моменту, когда её скорость расширения уменьшилась в 2 раза.
Решение
Верно использован закон сохранения импульса при расширении оболочки, после вспышки
звезды M 0V0  M 0  m
V0
, где m – масса межзвездного вещества, захваченного звездой
2
при ее расширении. Использована формула плотности межзвездного вещества,
захваченного звездой при ее расширении  
m
4 3
R
3
. Представлены алгебраические
преобразования для определения радиуса оболочки к тому моменту, когда её скорость
расширения уменьшилась в 2 раза R  3
3M 0
.
4
4
Задача №5.
«Бэтмен ловит преступника».
Бэтмен ловит преступника. На какую максимальную высоту они поднимутся, если
задержание произойдёт успешно?
Задача №6.
«Цикл Незнайкин профиль».
Изучая законы термодинамики, Незнайка настолько сильно увлёкся тепловыми
двигателями, что решил предложить свой собственный, в котором один моль идеального
одноатомного газа совершает циклический процесс «Незнайкин профиль» (контур
учебника физики в цикл не входит). Считая двигатель Незнайки идеальным, определить
максимально возможный КПД.
Решение:
Максимальная и минимальная температуры определяются с учётом того, что большей
температуре соответствует изотерма более удалённая от начала координат pV. Используя
5
уравнение Менделеева - Клапейрона, с учётом указанного масштаба, получаем, что
Tmax 
12 p0 9V0 108 p0V0
2 p0 2V0 4 p0V0
, Tmin 
.


R
R
R
R
Максимально возможный КПД  max 
Tmax  Tmin
 100%  96% .
Tmax
6
Задача №7.
«Механические колебания Смешариков».
Копатыч, Совунья, Лосяш, Крош, Пин и Нюша связаны между собой весомой
дружбой с помощью невесомых пружин жёсткостью k каждая, так, что они образуют
правильный шестиугольник.
Одновременно
всем шестерым смешарикам сообщают
одинаковые по модулю скорости, направленные от центра правильного шестиугольника.
Определить период колебаний весёлой компании, если масса каждого смешарика m0.
Задача №8.
«Странная линза».
Линза составлена из двух половинок. Верхняя часть линзы вырезана из линзы,
оптическая сила которой равна 1,5D0, нижняя - из линзы с оптической силой 2D0. Радиусы
кривизны обеих линз одинаковы. На расстоянии f= D0-1 на главной оптической оси
составной линзы расположена светящаяся точка. Сколько изображений даст такая линза,
где они будут расположены и какими они будут, действительными или мнимыми?
Считать, что на границе между половинками свет полностью поглощается. Линза является
тонкой.
7
Решение:
Каждая из половинок работает как отдельная собирающая линза, поэтому получается два
изображения. Для верхней линзы фокусное расстояние F 
источник света расположен на расстоянии d 
1
1
2


. Т.к.
D 1,5 D0 3D0
1
 F , то изображение получается
D0
действительным, расположенным на главной оптической оси и с учётом правил
построения на расстоянии f 
2
 2d от оптического центра линзы (см. рис.). Такой же
D0
результат получается, если использовать формулу тонкой линзы
f 
1 1 1
  , тогда
F d f
dF
2

 2d .
d  F D0
Для нижней линзы фокусное расстояние F 
на расстоянии d 
1
1

. Т.к. источник света расположен
D 2 D0
1
 F , то изображение получается действительным, расположенным
D0
на главной оптической оси и с учётом правил построения на расстоянии f 
1
 d от
D0
8
оптического центра линзы (см. рис.). Такой же результат получается, если использовать
формулу тонкой линзы
dF
1
1 1 1

d.
  , тогда f 
d  F D0
F d f
Для сравнения общий вид чертежа имеет вид:
Чёрный цвет соответствует верхней половине линзы, синий – нижней. Из последнего
рисунка видно, что изображение источника света, которая даёт нижняя линза,
расположено к оптическому центру ближе, чем изображение, которая даёт верхняя
половина линзы.
9
2009-2010 учебный год.
10 класс (за каждую задачу 10 баллов)
1. «Бросок камня». Камень бросают
поверхности горы, на которое
со скоростью V0 под углом  к
удалиться камень за время полета.
поверхности горы, составляющей
угол  с горизонтом (см. рис.1).
Найти:
1)
время
полета;
2)
дальность
полета;
3)
максимальное
расстояние
от
рис. 1
2. «Шары
в
воде».
Два
шара
одинакового объёма, но разной
массы: 5 кг и 2 кг соединены
нитью.
Определите
натяжение
нити, соединяющей шары, если
они
плавают
в
вертикальном
положении,
рис. 2
полностью
погрузившись в воду (см. рис. 2).
3. «Вода и лёд в калориметре». В калориметре находится 300 г воды при температуре
80 0С. В калориметр бросают 400 г льда, температура которого равна -5 0С.
Определить
содержимое
калориметра
при
установившейся
температуре.
Теплообменом с окружающей средой и теплоёмкостью калориметра пренебречь.
Удельная теплоёмкость воды 4200
Дж
Дж
, удельная теплоёмкость льда 2100
,
0
кг  С
кг  0 С
удельная теплота плавления льда 3,33∙105
4. «Сопротивление
фигур».
На
Дж
.
кг
проволочных
каркасов.
сколько сопротивление «Солнца»
Сопротивление каждого резистора
больше
1 Ом.
сопротивления
«парусника»
фигуры
(см.
рис.3)?
выполнены
в
Все
виде
10
рис. 3
11
5. Экспериментальная задача. Оценить объём одной скобы для степлера.
Оборудование: полоска скоб для степлера, линейка.
11 класс (за каждую задачу 10 баллов)
1. «Падение шарика в воде». Шарик плотностью , меньшей чем у воды, падает с
высоты H в воду. Сила сопротивления в воде составляет 1/3
веса шарика.
Пренебрегая силой сопротивления воздуха, определите, на какую максимальную
глубину шарик погрузится в воду. Плотность воды 0.
2. «Резиновый шар в воде». Тонкий резиновый шар радиуса R1=2 см заполнен
воздухом при температуре t1=20 0C и давлении p0=0,1 МПа. Каков будет радиус
шара R2, если его опустить в воду с температурой t1=4 0C на глубину h=20 м?
3. «Конденсатор в цепи постоянного тока». После замыкания ключа (см. рис. 1)
заряд конденсатора уменьшился в 1,5 раза. Найти внутреннее сопротивление
элемента, если R=10 Ом.
рис. 1
4. «Множество линз». Перед системой из 2009 одинаковых собирающих линз с
фокусным расстоянием F на расстоянии 2F находится предмет (см. рис. 2). Где
будет его изображение и каким оно будет? Расстояние между любыми соседними
линзами одинаково и равно 2F.
1
2
3
…………
2007
2008
2009
рис. 2
12
5. Экспериментальная задача. Оцените объём лазерного CD-диска.
Оборудование: два CD-диска, миллиметровка или линейка.
Решения
10 класс
1. Выбрать систему координат, разбить вектор ускорения свободного падения и вектор
начальной скорости по составляющим:
.
Уравнения движения по координатным осям имеют вид: x  V0  cos   t 
y  V0  sin   t 
Если
t
–
g  cos   t 2
.
2
время
полёта,
то
y=0,
0  V0  sin   t 
2V sin 
g  cos   t 2
,t 0
.
g cos 
2
Подставляя
полученное
выражение
x  V0  cos   t 
g  sin   t 2
,
2
получаем
l
g  sin   t 2
,
2

тогда
можно
времени
выражение
оценить
полёта
для
время
в
дальности
полёта:
уравнение
полёта:

V02
 sin 2  2tg  sin 2  .
g cos 
Для оценки максимального расстояния от поверхности горы считаем, что сопротивление
воздуха отсутствует, тогда время подъёма до неё в 2 раза меньше времени всего полёта:
t под 
V0 sin 
.
g cos 
Подставляя
выражение
времени
подъёма
в
уравнение
13
y  V0  sin   t 
g  cos   t 2
, получаем выражение для максимального расстояния от
2
поверхности горы: hmax 
V02 sin 2 
.
2 g cos 
Критерии оценивания
Выбрана система координат, верно записаны уравнения движения по координатным
осям………………………………………………………………………………………………4 балла
Верно получено выражение для времени полёта ………………………………………2 балла
Верно получено выражение для дальности полёта …………………………………..2 балла
Верно получено выражение для максимальной высоты …………………………….2 балла
2. Выполнить рисунок с указанием всех действующих сил:
Условия равновесия для нижнего и
верхнего шаров имеют вид: Fарх+T=m1g,
Fарх=T+m2g. Решая полученную систему
уравнений, получаем
выражение для
силы натяжения нити: T 
(m1  m2 )  g
,
2
T= 15 Н.
Критерии оценивания
Указаны направления всех действующих сил ………………………………………2 балла
Верно записаны условия равновесия …………………………………………………4 балла
Решена система уравнений и получен числовой результат…………………… 4 балла
3. Провести анализ тепловых процессов: а) количество теплоты, выделяющееся при
остывании воды до 0 0C Q1=c1m1(0-80)= -100 800 Дж; б) количество теплоты, необходимое
для нагревания льда до 0
0
C Q2=c2m2(0-(-5))=4 200 Дж; в) количество теплоты,
необходимое для плавления льда Q3=m2=133 200 Дж; г) получили Q1  Q2  Q3 ,
следовательно, часть льда расплавится и превратится в воду, а вся смесь будет находиться
при 0 0C. Тогда уравнение теплового баланса примет вид: Q1  Q2  Q3' , где Q’3= mлx количество теплоты, необходимое для расплавления части льда массой mлx. Получаем
mлx=0,29 кг. Тогда в сосуде останется льда: 0,4-0,29=0,11 кг, а воды: 0,3+0,29=0,59 кг.
14
Критерии оценивания
Рассчитано
количество
теплоты,
выделяющееся
при
остывании
воды
до
0 0C……………………………………………………………………………………………………1 балл
Рассчитано количество теплоты, необходимое для нагревания льда до 0 0C………1 балл
Рассчитано количество теплоты, необходимое для плавления льда ………………..1 балл
Проведен анализ тепловых процессов Q1  Q2  Q3 ……………………………………..2 балла
Записано уравнение теплового баланса Q1  Q2  Q3' ………………………………….. 2 балла
Рассчитана расплавленная часть льда …………………………………………………….1 балл
Рассчитана оставшаяся часть льда ………………………………………………………1 балл
Рассчитана образовавшаяся часть воды ………………………………………………..1 балл
4. Составим эквивалентную схему для «Солнца»:
R12=2 Ом, R123=2/3 Ом, R1-9=3∙2/3=2 Ом, R1-18= R1-9/2= 1Ом.
Составим эквивалентную схему для «парусника»:
R23=R2/2=2 Ом, R23,4,5=R23/3=2/3 Ом,
R1,6,7=R1/3=1/3 Ом,
R17 
R25  R167
2
 Ом ,
R25  R167 9
R810 
R8  R9  R10
2
 Ом ,
R8  R9  R8  R10  R9  R10 3
R1-10=R1-7+R8-10=8/9 Ом.
Следовательно, сопротивление «Солнца» больше сопротивления «парусника» на
величину, равную 1-8/9=1/9 Ом.
15
Критерии оценивания (допускается без эквивалентных схем)
Рассчитано сопротивление «Солнца» ………………………………………………5 баллов
Рассчитано сопротивление «парусника» и приведен верный ответ…………5 баллов
5.
Объём одной скобы V=abc, а – длина
скобы, b – ширина скобы, c – толщина
скобы. Измерив длину полоски L и
сосчитав количество N входящих в неё
скоб, можно определить ширину одной
скобы: b=L/N.
Отломив и распрямив одну из скоб,
определяем её длину a.
Для нахождения толщины c отделяем от
полоски n скоб, выпрямляем у них один
конец и накладываем одну на другую.
Измерив толщину полоски l, находим
толщину одной скобы: c=l/n.
Итак,
V  a
с
учетом
формул,
получаем
L l
 .
N n
Критерии оценивания
Описан метод определения длины одной скобы ………………………………………1 балл
Определена длина одной скобы …………………………………………………………..1 балл
Описан метод определения ширины скобы …………………………………………...2 балла
Определена ширина скобы ………………………………………………………………..1 балл
Описан метод определения толщины скобы …………………………………………2 балла
Определена толщина скобы ……………………………………………………………..1 балл
Определен объем одной скобы ………………………………………………………….2 балла
16
11 класс
1. При падении шарика в воздухе сопротивление не учитывается, следовательно, по
закону сохранения энергии выражение для скорости, с которой шарик начнет движение в
воде имеет вид V  2 gH . Движение шарика в воде описываем при помощи второго
закона Ньютона
.
В скалярном виде второй закон Ньютона
принимает вид: ma  mg 
mg
m
 0 g .
3

Ускорение, с которым движется шарик в
воде, заменяем используя безвременную
формулу
пути,
максимальной
конечная
a
учитывая,
глубине
скорость
что
соответствует
равная
нулю:
0 V 2
2 gH
gH


.После
2h
2h
h
преобразований,
получаем
выражение
для максимальной глубины погружения
шарика в воде: h 
3H
.
3 0  2 
17
Критерии оценивания
Использован закон сохранения энергии для определения скорости, с которой шарик начнёт движение в
воде …………………………………………………………………… 2 балла
Выполнен рисунок с указанием всех действующих сил ……………………………… 1 балл
Записан второй закон Ньютона в векторном виде, найдены проекции всех действующих сил, верно
расписаны
сила
сопротивления
в
воде,
сила
Архимеда
с
учётом
данных
задачи……………………………………………………………………………………………4 балла
Использована безвременная формула пути …………………………………………… 1 балл
Верно
выполнены
алгебраические
преобразования,
приводящие
к
верному
результату
……………………………………………………………………………………………………2 балла
2. Для неизменного количества воздуха в резиновом шарике, в двух состояниях используем уравнение
Клапейрона:
p1V1 p 2V2
, тогда

T1
T2
4
4
p 0 R13  p 0  gh  R23
3
3

. После преобразований, получаем
T1
T2
выражение для радиуса резинового шарика в оде на глубине h: R2  R1  3
p0T2
 1,37см .
T1  p0  gh 
Критерии оценивания
Верно выполнен перевод в СИ (радиус, температура в К) ………………………… 1 балл
Записано уравнение Клапейрона в общем виде ………………………………………..1 балл
Использована формула объёма шара ……………………………………………………1 балл
Верно записано давление воздуха, когда шарик находится на глубине ………….2 балла
Представлены алгебраические преобразования, приводящие к верному числовому результату
…………………………………………………………………………………..5 баллов
3. При разомкнутом ключе заряд на обкладках конденсатора равен: q1=CE. При замкнутом ключе:
q2=CU=CUR=CIR= C
E
R . По условию задачи q1/q2=1,5, тогда после преобразований получаем
Rr
r=0,5R=5 Ом.
Критерии оценивания
Верно записан закон Ома для участка цепи до замыкания ключа ……………………1 балл
Верно записан закон Ома для полной цепи после замыкания ключа …………………3 балла
Представлены алгебраические преобразования, приводящие к верному числовому результату
………………………………………………………………………………………6 баллов
18
4. Для тонкой линзы известно, что если предмет находится на двойном фокусе собирающей линзы, то
его изображение будет действительным, перевёрнутым, равным по величине и расположенным на
двойном фокусе за линзой. Таким образом, в рассматриваемой системе изображение предмета в первой
линзе будет находиться в плоскости второй линзы и окажется перевёрнутым. Следующее изображение
предмета совпадает с плоскостью четвёртой линзы и будет прямым. Следовательно, в рассматриваемой
системе линз изображение будет совпадать с плоскостью чётных линз, причем в линзах с номерами
2(2n+1) оно будет перевёрнутым, а в линзах с номерами 4n- прямым. Номер предпоследней линзы
чётный и делится на 4, поэтому изображение предмета окажется в плоскости 2008-й линзы или в
двойном фокусе 2009-й линзы и окажется прямым.
Критерии оценивания
Верно указаны характеристики изображения предмета, находящегося в двойном фокусе тонкой
собирающей линзы ………………………………………………………………………1 балл
Установлена зависимость перевёрнутого изображения с номерами линз 2(2n+1)…4 балла
Установлена зависимость прямого изображения с номерами линз 4n……………… 4 балла
Записан верный ответ ………………………………………………………………………… 1 балл
5. Объём лазерного диска V=(S1-S2)h, где S1=R2 – площадь диска с отверстием, S2=r2 – площадь
отверстия диска, h – толщина диска. Радиусы диска и отверстия измеряются либо по миллиметровке,
накладывая на неё диск, либо при помощи линейки. Для определения толщины ставим на ребро
несколько плотно сложенных дисков на миллиметровую бумагу или линейку. Определяем толщину H

нескольких (N) дисков. Тогда h=H/N. В итоге V   R 2  r 2
 HN . (V≈13,6 см3)
Критерии оценивания
Описан метод определения объёма диска, включая формулу V=(S1-S2)h …………2 балла
Определён радиус диска R …………………………………………………………………..2 балла
Определён радиус отверстия r ……………………………………………………………2 балла
Определена толщина диска ………………………………………………………………..2 балла
Верно рассчитан объём диска …………………………………………………………….2 балла
19
2011-2012 учебный год.
7 класс
Задача №1. (10 баллов)
«Рекорды в мире животных». В …. году состоялась 1-я олимпиада в мире животных. В спортивных
соревнованиях по скоростному движению по правилам Международной системы единиц (СИ) были
получены результаты: акула – 500 м/мин, бабочка – 8 км/ч, борзая – 16 м/с, гепард – 112 км/ч, заяц – 60
км/ч, ласточка – 17,5 м/с, муха - 300 м/мин, слон – 40 км/ч, улитка – 1,4 мм/с, черепаха – 6 м/мин. Кто
стал бронзовым призёром?
Задача №2. (10 баллов)
«Заезды автомобилей». Два автомобиля выехали одновременно из города и двигались по одной и той
же прямой дороге. На рисунке приведены графики зависимости пути от времени для этих автомобилей.
Определите: 1) в какие интервалы времени автомобили удалялись друг от друга? 2) в какие интервалы
времени автомобили сближались друг с другом? 3) в какой интервал времени расстояние между
автомобилями оставалось неизменным? Каким было это расстояние? 4) какова наибольшая скорость
путь (S, км)
автомобиля 1? 5) какова наименьшая скорость автомобиля 2?
70
60
50
40
30
20
10
0
0
10
20
30
40
50
60
70
время (t,мин)
ав томобиль 1
ав томобиль 2
Задача №3. (10 баллов)
«Забег экспериментатора Глюка». При подготовке к зачёту по физической культуре, экспериментатор
Глюк преодолел дистанцию 5 км. Первый километр он пробежал за 3 мин, а на каждый последующий
километр у него уходило на t секунд больше, чем на предыдущий. Найдите t, если известно, что
средняя скорость на всём пути оказалась такой, как если бы Глюк пробежал каждый километр за 3 мин
12 с.
20
Задача №4. (10 баллов)
«Плотность жидкости». Стеклянную мензурку уравновешивают на весах с помощью набора гирь
(рисунок а). Затем в мензурку наливают неизвестную жидкость, и опять уравновешивают ее на весах
(рисунок б). Чему равна плотность налитой в мензурку жидкости?
21
22
8 класс
Задача №1. (10 баллов)
«Волга-матушка». Определите скорость течения воды в Волге на участке, где скорость
грузового теплохода по течению равна 600 км/сут., а против течения – 336 км/сут.
Задача №2. (10 баллов)
«Кубок победителя». Статуэтка победителя олимпиады по физике отлита из золота и
алюминия - голова сделана из золота (плотность 19,3 г/см3), ее объем составляет 2/3
общего объема статуэтки, остальное - из алюминия (плотность 2,7 г/см3). Утонет ли
статуэтка в озере из жидкой ртути (плотность 13,6 г/см3)?
Задача №3. (10 баллов)
«Баловство маленьких близнецов». Две маленькие обезьянки, используя метод проб и
ошибок, привели систему (см. рисунок) в равновесие. Какова длина бруска АО, если ось
вращения находится в точке О, расстояние АВ равно 40 см, масса бруска 1 кг, масса левой
обезьянки 2 кг, а правой 3 кг. Блоки невесомы, трение в блоках отсутствует. Какие
простые механизмы представлены в системе?
23
Задача №4. (10 баллов)
«Теплоёмкость меди». Ученику восьмого класса предложили оценить удельную
теплоёмкость меди. Для этого ему дали медную кружку массой 200 г, имеющую
комнатную температуру 20 0С, и налили в неё кипяток массой 40 г. Через некоторое время
температура медной кружки и воды стали одинаковыми и равными 75 0С. Какое значение
удельной теплоёмкости меди получил ученик восьмого класса?
24
9 класс
Задача №1. (10 баллов)
«Поведение шарика в воздухе». Мальчик держит в руках шарик массой 3,87 г и объёмом 3
л. Что произойдёт с этим шариком, если его выпустить из рук?
Задача №2. (10 баллов)
«Заезды автогонщиков». В квалификационных заездах автогонщик перед соревнованиями
должен на протяжении четырех кругов показать среднепутевую скорость 200 км/ч. Из-за
сбоев в работе двигателя среднепутевая скорость автомобиля на первых двух кругах
оказалась равной 170 км/ч. С какой среднепутевой скоростью гонщик должен пройти два
последних круга?
Задача №3. (10 баллов)
«Необычный водопад». Оценить реальность существования водопада на Земле, чтобы
вода у основания полностью испарялась? Необходимые постоянные для решения задачи
можно узнать из справочного материала. Начальную температуру принять за 5 0С.
Задача №4. (10 баллов)
«Сопротивление
резисторов».
Общее
сопротивление
двух
резисторов
при
их
последовательном соединении составляет 10 Ом, а при их параллельном соединении 2,1
Ом. Определить сопротивление каждого резистора.
25
10 класс
Задача №1. (10 баллов)
«Движение Глюка». Экспериментатор Глюк, двигаясь равноускоренно на автомобиле, за
первые 5 с своего движения проехал путь 100 м, а за первые 10 с – 300 м. Определите с
какой скоростью начал движение автомобиль Глюка?
Задача №2. (10 баллов)
«Движение друзей». Винни-Пух и Пятачок держатся за
легкую
нерастяжимую нить, перекинутую через невесомый блок. В начальный
момент времени блок заторможен, а расстояние между ними по вертикали
49 см, причем Винни-Пух расположен выше. Через какое время друзья
окажутся на одной горизонтали, если системе позволить двигаться? Масса
Винни-Пуха 600 г, а Пятачка – 400 г. Трением пренебречь.
Задача №3. (10 баллов)
«Бедная муха». Оценить, с какой скоростью должна лететь муха, чтобы, ударившись об
оконное стекло, от нее «ни осталось бы и мокрого места»? Необходимые постоянные для
решения задачи можно узнать из справочного материала.
Задача №4. (10 баллов)
«Плавление льда на алюминиевой проволоке с током». Алюминиевая проволока
диаметром d = 2,5 мм, не слишком гнутая, покрыта льдом. Общий диаметр проволоки со
льдом равен D = 3,5 мм. Температура льда и проволоки t = 0 °С. По проволоке пустили
ток силой I = 15 А. За какое время лёд растает? Плотность льда ρл = 0,9 г/см3, а его
удельная теплота плавления λ = 340 кДж/кг. Удельное сопротивление алюминия
ρ = 2,8∙10–8 Ом∙м.
26
Задача №5. (10 баллов)
«Странная удельная теплоёмкость». На рисунке приведен график зависимости удельной
теплоемкости c некоторого тела от его температуры t. Какое количество теплоты Q нужно
сообщить этому телу для того, чтобы повысить его температуру от t1 = 20 °C до t2 = 80 °C?
Масса тела m = 1 кг.
11 класс
Задача №1. (10 баллов)
«Экспериментатор Глюк на арене цирка». В
цирковом
номере
экспериментатор
цирковом
«Мёртвая
Глюк
автомобиле,
на
должен
полупетля»,
небольшом
преодолеть
полупетлю. Своё движение без трения по
внутренней поверхности желоба в форме
окружности радиусом R=14 м он начал со
скоростью 72 км/ч. Но в виду недостаточной
скорости, номер не удался. Определить, на какой высоте h от горизонтальной поверхности
произошёл отрыв циркового автомобиля экспериментатора Глюка.
Задача №2. (10 баллов)
«Метеорное тело». Оценить минимальную скорость, с которой метеорное тело, влетая в
атмосферу Земли, полностью испаряется? Необходимые постоянные для решения задачи
можно узнать из справочного материала.
27
Задача №3. (10 баллов)
«Электрическая
полупроводниковыми
цепь
с
диодами».
идеальными
В
схеме,
изображённой на рисунке, амперметр показывает силу
тока 1 А. Какую силу тока покажет амперметр при
смене
полярности
источника
тока?
Внутренним
сопротивлением источника и амперметра пренебречь.
Полупроводниковые диоды считайте идеальными. Сопротивления резисторов R1=4 Ом,
R2=1 Ом, R3=3 Ом.
Задача №4. (10 баллов)
«Электромагнитный ускоритель». Электромагнитный ускоритель представляет собой два
провода, расположенные в горизонтальной плоскости на расстоянии 20 см друг от друга,
по которым может скользить без трения металлическая перемычка АС массой 2 кг.
Магнитное поле с индукцией B=1 Тл перпендикулярно плоскости движения перемычки.
Какой ток следует пропустить по перемычке, чтобы она, пройдя путь 2 м, приобрела
скорость 10 м/с?
Задача №5. (10 баллов)
«А где линза?». В своих старых записях по оптике, экспериментатор Глюк, обнаружил
рисунок на котором показана стрелка АВ и её изображение А1В1 в линзе. Из-за
длительного времени, часть рисунка выцвела. Помогите Глюку полностью восстановить
первоначальный рисунок, а именно, построением определить тип и положение линзы, её
оптического центра и главных фокусов.
28
Решения задач и критерии оценивания для 7 класса
Задача №1.
Т.к.
спортивные
соревнования
по
скоростному
бегу
проходят
по
правилам
Международной системы единиц (СИ), то все скорости переводим в м/с: акула – 8,3 м/с,
бабочка – 2,2 м/с, борзая – 16 м/с, гепард – 31,1 м/с, заяц – 16,7 м/с, ласточка – 17,5 м/с,
муха – 5 м/с, слон – 11,1 м/с, улитка – 0,0014 м/с, черепаха – 0,1 м/с. Бронзовый призёр
(третий лучший результат) стал заяц.
Критерии оценивания:
Числовые
значения
участников
скоростного
бега
представлены
в
Международной системе единиц (СИ). За каждого участника 1 балл (кроме 8 баллов
борзой и ласточки)
Верно указан бронзовый призёр
2 балла
Задача №2.
Решение и критерии оценивания:
Указан интервал времени, в течение которого автомобили удалялись друг от друга
(от 0 до 20 мин)
2 балла
Указан интервал времени, в течение которого автомобили сближались друг с
другом (от 40 до 60 мин)
2 балла
Указан интервал времени, в течение которого расстояние между автомобилями
оставалось неизменным (от 20 до 40 мин)
1 балл
Указано числовое значение неизменного расстояния между автомобилями (20 км)
1 балл
Определена и рассчитана наибольшая скорость автомобиля 1 (2 км/мин)
2 балла
Определена и рассчитана наименьшая скорость автомобиля 2 (0,5 км/мин)
2 балла
Задача №3.
Рассчитаем среднюю скорость Глюка, если по условию задачи каждый километр он
пробегает за 3 мин 12 с (192 с), то по определению средней скорости получаем
Vср 
S весь 5000 м
м

 5,2 . С учётом того, что на прохождение первого километра он
t всё
5  192с
с
затратил 3 мин (180 с), а на каждый последующий километр у него уходило на t секунд
больше, чем на предыдущий, то общее время пробега 5 км можно представить
выражением:
29
t всё  t1  t 2  t 3  t 4  t 5  180  180  t   180  t  t   180  t  t  t   180  t  t  t  t   900  10t
, тогда новое выражение для рассчитанной средней скорости имеет вид:
Vср 
S весь
5000


t всё
900  10t
5,2 
5000
5000
 900  10t 
 900  10t  962  10t  962  900  10t  62  t  6(c)
900  10t
5,2
.
Критерии оценивания:
Верно рассчитана средняя скорость Глюка (5,2 м/с)
2 балла
Верно записано выражение времени при условии, что на каждый последующий
километр у Глюка уходило на t секунд больше, чем на предыдущий 3 балла
t всё  900  10t
Представлено выражение 5,2 
5000
900  10t
2 балла
Получен числовой результат t  6(c)
3 балла
Задача №4.
Решение и критерии оценивания:
Определена масса пустой мензурки (55 г)
2 балла
Определена масса мензурки с жидкостью (118 г)
2 балла
Определена масса жидкости (63 г)
2 балла
Определен объём жидкости (50 мл = 50 см3)
2 балла
Рассчитана плотность жидкости  
m
63г
г

 1,26 3 или 1260 кг/м3
3
V 50см
см
2 балла
Решения задач и критерии оценивания для 8 класса
Задача №1.
Выражение для скорости грузового теплохода по течению V1  Vгр.теп  V реки , V1=600
км/сут, выражение для скорости грузового теплохода против течения V2  Vгр.теп  V реки ,
V2=336
км/сут.
V1  V2  2V реки V реки
Решая
систему
уравнений,
получаем
V1  V2
км
 132
.
2
сут
Критерии оценивания:
Записано
выражение
для
скорости
грузового
теплохода
по
течению 3 балла
30
V1  Vгр.теп  V реки
Записано выражение для скорости грузового теплохода против течения 3 балла
V2  Vгр.теп  V реки
Представлены
алгебраические
преобразования
для
системы
уравнений при водящие к выражению для скорости реки V реки
полученных
3 балла
V1  V2
2
Получен числовой результат Vреки=132 км/сут
1 балл
Задача №2.
Рассчитаем среднюю плотность статуэтки победителя олимпиады по физике и сравним её
с плотностью ртути:
 ср 
m mголовы  mостальное


V
V
2
3
1
3
 золото  V   алюм иний  V
V

2   зол   ал
г
 13,77 3 .
3
см
Расчёты показывают, что средняя плотность статуэтки победителя олимпиады по физике
оказалась больше плотности ртути, поэтому она утонет в озере из жидкой ртути.
Критерии оценивания:
Рассчитана средняя плотность статуэтки победителя олимпиады по физике
6 баллов
(13, 77 г/см3)…
Использовано условие плавания тел (сравнение плотностей) для ответа на
вопрос задачи (статуэтки победителя олимпиады по физике утонет в озере
из жидкой ртути, т.к. средняя плотность статуэтки оказалась больше
плотности ртути)
4 балла
Задача №3.
На
рисунке
представлены
следующие
простые
механизмы:
подвижный
блок,
неподвижный блок, рычаг второго рода. Введём обозначения: m1 – масса левой обезьянки,
m2 – масса правой обезьянки, M – масса рычага, l – длина рычага, l0 – расстояние AB. Т.к.
один подвижный блок даёт выигрыш в силе в 2 раза, то к точке А рычага приложена сила
натяжения нити равная половине силы тяжести, действующей на левую обезьянку, т.е.
T
m1 g
и её плечо относительно оси вращения (т. О) равно l (длине рычага). Плечо
2
силы тяжести, действующей на правую обезьянку (m2g) относительно т. О равно (l-l0).
Плечо силы тяжести, действующей на рычаг относительно т. О равно
l
. Для рычага
2
31
второго
рода
относительно
точки
О
правило
моментов
имеет
вид:
m1 g
l
 l  m2 g  l  l0   Mg  . После преобразований, получаем выражение для длины
2
2
рычага l 
2m 2 l 0
и числовое значение l=48 см.
2m2  M  m1
Критерии оценивания:
Указан простой механизм – подвижный блок
0,5 балла
Указан простой механизм – неподвижный блок
0,5 балла
Указан простой механизм – рычаг (возможен вариант рычаг второго рода)
0,5 балла
Использовано свойство подвижного блока для выражения T 
m1 g
2
1,5 балла
Верно указано плечо силы Т относительно т.О (l)
0,5 балла
Записано выражение силы тяжести, действующей на правую обезьянку (m2g)
0,5 балла
Верно указано плечо силы m2g относительно т.О (l-l0)
0,5 балла
Записано выражение силы тяжести, действующей на рычаг (Mg)
0,5 балла
Верно указано плечо силы Mg относительно т.О (
l
)
2
1 балл
Верно записано для рычага второго рода относительно точки О правило
моментов:
3 балла
m1 g
l
 l  m2 g  l  l0   Mg 
2
2
Представлены
результату l 
алгебраические
преобразование,
приводящие
к
верному
2m 2 l 0
, l=48 см
2m2  M  m1
1 балл
Задача №4.
Введём обозначения: масса медной кружки m1=200 г=0,2 кг, её начальная температура
t1=20 0С, её удельная теплоёмкость, которую необходимо определить c1, масса кипятка
m2=40 г=0,04 кг, его температура t2=100 0С, удельная теплоёмкость воды с2=4200
Дж
,
кг  0 С
температура, после установления состояния теплового равновесия t3=75 0С.
Критерии оценивания:
Верно записано уравнение теплового баланса c1m1 t3  t1   c2 m2 t 3  t 2 
6 баллов
Верно записано выражение для расчёта удельной теплоёмкости меди
2 балла
32
c1 
c2 m2 t 2  t 3 
m1 t 3  t1 
Верно получено числовое значение удельной теплоёмкости меди с1=382
2 балла
Дж
кг  0 С
Решения задач и критерии оценивания для 9 класса
Задача №1.
Решение и критерии оценивания:
Верно рассчитана плотность шарика  
m 0,00387кг
кг

 1,29 3 (или сила
3
V
0,003 м
м
тяжести 0,0387 Н)
3 балла
Из справочного материала, верно указана плотность воздуха (т.к. название
задачи «Поведение шарика в воздухе»)  воздуха  1,29
кг
(или рассчитана сила 3 балла
м3
Архимеда 0,0387 Н)
Использовано условие плавания тел (сравнение плотностей или сравнение
силы тяжести и силы Архимеда) для ответа на вопрос задачи (шарик зависнет 4 балла
в покое)
Задача №2.
Введём обозначения: среднепутевая скорость на протяжении четырёх кругов Vср=200
км/ч, среднепутевая скорость на протяжении первых двух кругов V12=170 км/ч,
среднепутевая скорость на протяжении последних двух кругов V34.
Решение и критерии оценивания:
Верно представлено выражение для средней скорости на протяжении четырех
кругов
2 балла
4S
Vср 
t1  t 2  t 3  t 4
Верно представлено выражение для среднепутевой скорости автомобиля на 2 балла
33
первых двух кругах V12 
2S
t1  t 2
Верно представлено выражение для среднепутевой скорости автомобиля на
последних двух кругах V34 
2 балла
2S
t3  t 4
Представлены алгебраические преобразования для расчёта среднепутевой
скорости автомобиля на последних двух кругах V34 
Vср  V12
2 балла
2V12  Vср
Верно получено числовое значение среднепутевой скорости автомобиля на
последних двух кругах V34  243
км
ч
2 балла
Задача №3.
Решение и критерии оценивания:
Из справочного материала записаны и использованы: удельная теплоёмкость
воды 4 200
Дж
, удельная теплота парообразования воды 2,3∙106 Дж/кг,
0
кг  С
температура
кипения воды 100 0С (полагаем, что тепловые процессы происходят при
нормальном
атмосферном давлении)
Верно записан закон превращения механической энергии в тепловую энергию
mgh  cmt  t 0   rm
2 балла
4 балла
Представлены алгебраические преобразования для расчёта высоты водопада
h
ct  t 0   r
g
Верно получено числовое значение высоты водопада h  270 км
Верно сформулирован вывод о реальности существования подобного
водопада на Земле (невозможно)
2 балла
1 балл
1 балл
Задача №4.
Решение и критерии оценивания:
Верно составлено уравнение для последовательного соединения двух
резисторов
3 балла
34
Верно составлено уравнение для параллельного соединения двух резисторов
Представлены алгебраические преобразования для расчета сопротивления
резисторов
Получен верный результат (3 Ом, 7 Ом)
3 балла
3 балла
1 балл
Решения задач и критерии оценивания для 10 класса
Задача №1.
Введём обозначения: t1=5 c, S1=100 м, t2=10 c, S2=300 м, V0 – начальная скорость, с
которой начал движение автомобиль Глюка.
Решение и критерии оценивания:
Дважды
использованы
формулы
пути
равноускоренного
движения
автомобиля Глюка
2 балла
a  t12
a  t 22
S1  V0  t1 
, S 2  V0  t 2 
2
2
Представлены алгебраические преобразования для определения начальной
скорости
7 баллов
S  t 2  S1  t 22
V0  2 1
t1  t 2  t1  t 2 
Получено верное числовое значение начальной скорости автомобиля Глюка
V0=10 м/с
1 балл
Задача №2.
Обозначим массу Винни-Пуха через m1=600 г = 0,6 кг, массу Пятачка – m2=400 г = 0,4 кг,
первоначальное расстояние между ними – h=49 см=0,49 м. Если системе позволить
двигаться, то до момента, когда друзья окажутся на одной горизонтали, каждый из них
пройдёт
расстояние
равное
h
.
2
Движение
Винни-Пуха
и
Пятачка
является
равноускоренным, то используется уравнение координаты равноускоренного движения из
состояния покоя
h a t2

. Т.к. нить нерастяжимая, то ускорения, с которым они
2
2
движутся одинаковые. По условию задачи блок является неподвижным, невесомым,
трение в блоке отсутствует и нить невесомая, то сила натяжения нити по обе стороны от
оси блока одинаковые.
Решение и критерии оценивания:
35
Верно использовано и обосновано применение уравнения координаты
равноускоренного движения одного из друзей из состояния покоя
h a t2

2
2
Верно записан второй закон Ньютона в векторном виде для Винни-Пуха и
Пятачка
Выбрана ИСО (ось OY) и правильно найдены проекции действующих сил
на выбранное направление
2 балла
2 балла
2 балла
Представлены алгебраические преобразования для расчёта ускорения, с
которым движутся друзья a  g 
m1  m2
м
 1,96 2
m1  m2
с
2 балла
Верно определено время, через которое друзья оказались на одной
горизонтали t 
2 балла
h
 0,5c
a
Задача №3.
Решение и критерии оценивания:
Указан факт состава мухи из воды, что объясняет выбор учащимся
табличных данных: комнатная температура t0=20 0C, температура кипения
воды t=100 0C, удельная теплоёмкость воды с=4 200
теплота парообразования воды r  2,3  10 6
Дж
, удельная
кг  0 С
Дж
кг
2 балла
Верно указаны тепловые процессы (возможен вариант в виде записи
необходимых формул), а именно нагревание воды от комнатной
температуры до температуры кипения и последующее испарение
2 балла
Верно записан закон превращения механической энергии в тепловую
энергию
2 балла
m V 2
 c  m  t  t 0   r  m
2
Верно
получено
выражение
для
расчёта
скорости
мухи
V  2  c  t  t 0   r 
2 балла
Верно получено числовое значение скорости мухи V≈2,3 км/с
2 балла
36
Задача №4.
Решение и критерии оценивания:
Верно записан закон превращения электрической энергии в тепловую
энергию
(тепловым
расширением
алюминиевой
проволоки
будем
пренебрегать) I 2  R  t    m
2 балла
Верно записана формула электрического сопротивления алюминиевой
проволоки
R
l
 d2
2 балла
(l – длина проволоки)
4
Верно представлена масса льда, которая покрывает проволоку
   D2
  d 2  л   l

m л   л  Vл   л  Vобщ  Vал    л  
l 
 l  
 D2  d 2
4
4
 4


Верно
представлены
выражение
t
для
алгебраические
расчёта
времени,
преобразования
за
которое
и

2 балла
получено
лёд
растает
   л   2  d 2  D 2  d 2 
16  I 2  
2 балла
Верно получено числовое значение времени t≈19 мин
2 балла
Задача №5.
Вариант возможного решения и критерии оценивания:
Геометрическая интерпретация графической зависимости постоянной
удельной теплоёмкости вещества от температуры:
Q  c  m  t 2  t1   m  c  t 2  t1   m  S прям оугольника .
5 баллов
В общем случае Q  m  S фигуры .
Верно
использована
геометрическая
интерпретация
графической
зависимости удельной теплоёмкости вещества от температуры для решения
задачи:
прям оугольной
Q  m  S трапеции
5 баллов
1
1
Дж
 m   c1  c 2   t 2  t1   1кг   2  10 3  3  10 3
80  200 С  150кДж
0
2
2
кг  С


37
Решения задач и критерии оценивания для 11 класса
Задача №1.
Решение и критерии оценивания:
Для моментов соответствующих началу движения и отрыву от желоба верно
записан закон сохранения полной механической энергии
трения и с учётом выбора нулевого уровня):
(в отсутствие
m  V02 m  V 2

 mgh
2
2
2 балла
В момент отрыва автомобиля от внутренней поверхности желоба на высоте h,
сила реакции опоры равна нулю, поэтому второй закон Ньютона в векторном
2 балла
виде принимает вид: m  g  m  aц .с
Выбрана ИСО (OY), верно записан второй закон Ньютона в скалярном виде:
mg  sin  
m V 2
R
Использованы
2 балла
тригонометрические
соотношения
в
прямоугольном
треугольнике:
sin  
hR
R
2 балла
Представлены алгебраические преобразования для получения формулы
высоты
h
V02  gR
3g
Верно получено числовое значение высоты h=18 м
1 балл
1 балл
38
Задача №2.
Решение и критерии оценивания:
Указан факт состава метеорного тела из железа, что объясняет выбор
учащимся табличных данных: начальная температура t0=5 K (-268 0C), при
решении задачи возможен вариант не более 10 К, удельная теплоёмкость
железа с=460
Дж
, температура плавления железа tплавления=1539 0C,
0
кг  С
удельная теплота плавления железа =270 000
жидкого железа tкипения=3200
r  6,3  10 6
0
Дж
, температура кипения
кг
C, удельная теплота испарения железа
Дж
кг
Верно указаны тепловые процессы (возможен вариант в виде записи
необходимых формул), а именно нагревание железа до температуры
плавления, плавление железа, нагревание жидкого железа до температуры
испарения, испарение железа
2 балла
(за каждый
процесс
0,5 балла)
2 балла
Верно записан закон превращения механической энергии в тепловую
энергию
m V 2
 c  m  t плавления  t 0     m  c  m  t кипения  t плавления  r  m
2
2 балла
Верно получено выражение для расчёта скорости метеорного тела
V  2  c  t кипения  t 0     r 
2 балла
Верно получено числовое значение скорости метеорного тела при начальной
температуре t0=5 K (-268 0C): V≈4 км/с
2 балла
Задача №3.
До смены полярности оба идеальных полупроводниковых
диода работают в режиме «прямого тока», их сопротивление
равно нулю, что приводит к выравниванию потенциалов
точек A и B, C и D. После соответствующего соединения
точек равного потенциала, эквивалентная схема имеет вид:
39
При смене полярности оба идеальных полупроводниковых
диода
работают
в
режиме
«обратного
тока»,
их
сопротивление бесконечно велико (электрический ток через
них «не течёт»), поэтому эквивалентная схема имеет вид:
Решение и критерии оценивания:
Обоснованно представлена эквивалентная схема параллельного соединения
резисторов до смены полярности источника постоянного тока
2 балла
Верно определено полное сопротивление внешней цепи до смены
полярности источника постоянного тока Rобщ1 
R1 R2 R3
12
 Ом
R1 R2  R2 R3  R1 R3 19
1 балл
Верно записан закон Ома для полной цепи до смены полярности источника
постоянного тока I 1 
Обоснованно

1 балл
Rобщ1
представлена
эквивалентная
схема
последовательного
соединения резисторов после смены полярности источника постоянного
тока
2 балла
Верно определено полное сопротивление внешней цепи после смены
полярности источника постоянного тока Rобщ2  R1  R2  R3  8Ом
1 балл
Верно записан закон Ома для полной цепи после смены полярности
источника постоянного тока I 2 

Rобщ2
1 балл
Представлены алгебраические преобразования для расчёта показаний
амперметра после смены полярности источника постоянного тока и
получен верный результат I2≈0,08 А
2 балла
Задача №4.
Введём обозначения: длина металлической перемычки AC l=20 см=0,2 м, масса
перемычки m=2 кг, магнитная индукция B=1 Тл, путь, пройденный перемычкой S=2 м,
начальная скорость V0=0 м/с, приобретённая скорость V=10 м/с.
Решение и критерии оценивания:
40
Верно записан второй закон Ньютона в векторном виде
Выбрана
ИСО,
верно
найдены
проекции
2 балла
действующих
сил
на
горизонтальное направление
2 балла
FА  ma
Использована формула силы Ампера FA  IBl sin 90 0  IBl
2 балла
Использована безвременная формула пути при равноускоренном движении
перемычки из состояния покоя S 
V2
2a
2 балла
Представлены алгебраические преобразования для величины тока через
перемычку
I
1 балл
mV 2
2SBl
Верно получено числовое значение величины электрического тока через
перемычку
1 балл
I=250 A
Задача №5.
Вариант возможного решения и критерии оценивания:
Обоснованно
указан
тип
линзы
(перевёрнутое,
действительное
изображение может давать только собирающая линза)
1 балл
Верно найдены построением положение оптического центра т. О, точки,
лежащей на главной плоскости линзы т. С и правильно проедена главная
плоскость собирающей линзы
41
3 балла
Перпендикулярно главной плоскости линзы (СО) проведена главная
оптическая ось О1О2. Из точки В, параллельно главной оптической оси
проведён луч BD. После преломления в тонкой собирающей линзе, луч
пройдёт через т. B1 (изображение т. В). Точка пересечения DB1 и О1О2
определяет положение главного фокуса тонкой собирающей линзы.
3 балла
Из точки В1, параллельно главной оптической оси проведён луч B1К. После
преломления в тонкой собирающей линзе, луч пройдёт через т. B
(обратимость хода светового луча). Точка пересечения КB и О1О2 определяет
положение другого главного фокуса тонкой собирающей линзы.
42
3 балла
2013-2014 учебный год
11 класс
11 класс
Задача №1. «Горка».
Имеется абсолютно гладкая закрепленная горка, склон которой представляет собой дугу
окружности радиуса R (R много больше высоты горки). Найти время, за которое
небольшое тело съедет с горки без начальной скорости.
Задача №2. «Объем сосуда».
Расположенный горизонтально цилиндрический сосуд заполнен гелием и разделен на две
равные части закрепленным массивным поршнем. В частях сосуда находятся один и два
моля газа при одинаковой температуре. После освобождения поршень начинает скользить
без трения по стенкам цилиндра. Найти отношение объемов частей сосуда в момент, когда
поршень достигнет максимальной скорости. Считать, что изменение параметров газа в
каждой части сосуда происходит по адиабатическому закону pV5/3 =const.
Задача №3. «Вольтметр».
Один любознательный школьник раздобыл очень хороший вольтметр (то есть вольтметр с
очень большим внутренним сопротивлением), батарейку и резистор с сопротивлением 4
Ом. Когда он подключил вольтметр к клеммам батарейки, вольтметр показал напряжение
4,5 В. Затем он параллельно вольтметру подключил резистор, и показания вольтметра
уменьшились до 3,6 В. Чему равны ЭДС и внутреннее сопротивление батарейки?
Задача №4. «Проводник с током».
Определить модуль силы, действующей на проводник с током силой I, согнутый под
прямым углом. Расстояние между концами проводника равно L. Проводник находится в
однородном магнитном поле индукцией B. Вектор магнитной индукции перпендикулярен
плоскости, в которой лежит проводник.
43
Задача №5. «Линза».
Два луча симметрично пересекают главную оптическую ось собирающей линзы на
расстоянии d = 7,5 см от линзы под углом  = 4о. Определите угол  между этими лучами
после прохождения ими линзы, если фокусное расстояние линзы F = 10 см.
11 класс
1. Решение.
Данная система аналогична малым колебаниям математического маятника: роль
натяжения нити играет реакция опоры, направленная к центру окружности, а роль длины
подвеса – радиус окружности. Если справа симметрично поставить вторую такую же
горку, система будет совершать колебания в образовавшейся чаше с периодом T  2
, а в вершины горки съедет за четверть этого периода: t 
T 

4 2
R
g
R
.
g
2. Решение.
После освобождения поршень начнет скользить в сторону отсека с меньшим давлением.
Разгон будет продолжаться до тех пор, пока не выровняются давления по обе стороны от
поршня.
Уравнение Менделеева - Клапейрона: p 2V0  2RT0 , p1V0  1RT0 . Т.к. pV5/3=const, то для
газа в левой части цилиндрического сосуда p 2 V0 
цилиндрического сосуда p1 V0 
5
3
5
3
 pV2  3 , а для газа в правой части
5
 pV1  3 . После преобразований, отношение большего
5
объема к меньшему равно 23/5.
3. Решение.
Поскольку внутреннее сопротивление вольтметра очень велико, то при первом измерении
его показания соответствуют величине ЭДС батареи: Е=4,5 В. После подключения
44
резистора ток течет практически только через резистор, показания вольтметра
соответствуют
напряжению
r
преобразований
на
резисторе,
поэтому
U  IR 
E
R
Rr .
После
E  U  R
U
, r=1 Ом.
4. Решение.
По теореме Пифагора F  Fa2  Fb2  IB a 2  b 2  IBL .
5. Решение. Построим ход одного из данных лучей после преломления в линзе.
Введём дополнительные обозначения:
45
Рассмотрим прямоугольные треугольники:
1) KAB  tg
2) SKO  tg
3) OAC  tg

2

2

2

AB

 AB  F  tg
F
2,

KO BC


 BC  d  tg
d
d
2,

AC AB  BC

.
F
F
После преобразований:
tg

2

F  tg

2
 d  tg
F

2  tg   F  d  tg     2arctg   1,7  102 рад 1o .
2
F
2
2
Эту задачу можно решить и с использованием формулы линзы.
2014-2015 учебный год
11 класс
Задача №1 (10 баллов).
«Бэтмен ловит преступника».
Бэтмен ловит преступника. На какую максимальную высоту они поднимутся, если: 1) в
момент задержания преступник замер неподвижно от испуга; 2) задержание произойдёт
успешно?
46
Задача №2 (10 баллов).
«Исследования на новой планете».
Астронавты, исследуя воздух открытой ими планеты, нагрели порцию воздуха массой m =
200 г на ∆T = 60 0C один раз при постоянном давлении, а другой раз — при постоянном
объёме. Оказалось, что при постоянном давлении требуется подвести на ∆Q = 1 кДж
больше тепла, чем при постоянном объёме. Найдите среднюю молярную массу воздуха,
считая его идеальным газом.
Задача №3 (10 баллов).
«Изменение мощности».
Как изменится мощность на резисторе R1 после замыкания ключа, если R1= R2=R3=1 Ом,
внутреннее сопротивление источника постоянного тока r=0,5 Ом?
Задача №4 (10 баллов).
«Замкнутый виток в изменяющемся магнитном поле».
В однородном магнитном поле в плоскости, перпендикулярной линиям индукции поля,
находится замкнутый виток провода в виде окружности диаметром D=20 см. Провод в
сечении имеет диаметр d0=2 мм. Магнитное поле равномерно уменьшается со скоростью
B/t=1,09 Тл/с, что приводит к возникновению в витке индукционного тока Ii=10 А.
Определить удельное сопротивление проводника, из которого изготовлен виток.
Задача №5 (10 баллов).
«Наблюдение за яхтой».
Загорающий на скале человек разглядывает стоящую неподалёку яхту. Лучи от верхушки
мачты, попадающие к нему в глаза, образуют с горизонтом угол =170. Лучи от верхушки
мачты, попадающие к нему в глаза после отражения от поверхности воды, образуют с
горизонтом угол =250. Какова высота мачты над уровнем моря, если глаза человека
находятся на высоте 3 м над уровнем воды?
47
Решения задач школьного тура олимпиады по физике
11 класс
Задача №1 (10 баллов).
«Бэтмен ловит преступника».
Решение
Введём обозначения: M – масса Бэтмена, m – масса преступника, h – начальная высота, на
которой находился Бэтмен, Hmax – максимальная высота, на которую поднимутся Бэтмен и
преступник после успешного задержания, V – скорость Бэтмена на горизонтальном уровне
в момент перед задержанием преступника, U – скорость совместного движения Бэтмена и
преступника на горизонтальном уровне в момент сразу после задержания.
Скорость
Бэтмена в момент перехода на горизонтальный уровень определяем из закона сохранения
MV 2
м
 V  2 gh  10 . Скорость совместного
полной механической энергии Mgh 
2
с
движения Бэтмена и преступника на горизонтальном уровне определяем при помощи
закона сохранения импульса MV  M  m U  U 
MV
16 м

. Максимальную
M  m  3 с
высоту, на которую поднимутся Бэтмен и преступник после успешного задержания
относительно горизонтального уровня определяем при помощи закона сохранения полной
механической энергии
M  mU 2  M  mgH
max
2
 H max 
U2
 1,4 м .
2g
48
Задача №2 (10 баллов).
«Исследования на новой планете».
Решение
При постоянном давлении первый закон термодинамики с учётом преобразований
принимает вид: Q p 
условию

5 m
3 m
  R  T , а при постоянном объёме: QV    R  T . По
2 
2 
Q p  QV  Q ,
задачи
следовательно,
после
преобразований
mRT
г
 100
.
Q
моль
Задача №3 (10 баллов).
«Изменение мощности».
Решение
2
До
замыкания
ключа



 R1 ,
P1  I R1  
 R1  R2  r 
2
1
после
замыкания
ключа
2





2

 R . Введём обозначение R = R =R =1 Ом=R и найдём
P2  I 2 R1 
1
2
3
0

 1
R2 R3
r
 R1 
R2  R3


2R0  r 
P
P2
, после преобразований получаем 2 
 1,5625 .
P1 1,5R0  r 2
P1
2
отношение
Ответ: увеличится в 1,5625 раз
Задача №4 (10 баллов).
«Замкнутый виток в изменяющемся магнитном поле».
Ответ: 1,7∙10-8 Ом∙м,  
B Dd 2

.
t 16 I i
49
Задача №5 (10 баллов).
«Наблюдение за яхтой».
Решение
Выполним рисунок с учётом условия задачи и с учётом закона отражения света:
Из геометрических соображений: H  a  tg , h  b  tg , H  h  a  b  tg . После
преобразований получаем выражение для расчёта высота мачты над уровнем моря
H  h
tg  tg
0,4663  0,3057
 14,4 м .
. После подстановки числовых значений H  3м 
tg  tg
0,4663  0,3057
50