LO6_T

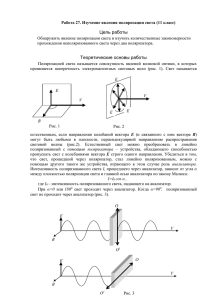
ЛАБОРАТОРНАЯ РАБОТА №6
ИССЛЕДОВАНИЕ ИНТЕНСИВНОСТИ ПОЛЯРИЗОВАННОГО
СВЕТА, ПРОШЕДШЕГО ЧЕРЕЗ АНАЛИЗАТОР
(ЗАКОН МАЛЮСА)
1.Цель работы: ознакомление со свойствами поляризованного света и
проверка закона Малюса
2. Теория вопроса
Как известно, световые волны поперечны; электрический вектор
Е и магнитный вектор Н (Н  E) располагаются в плоскости, перпендикулярной к направлению распространения волны (лучу S). Во всякой
данной точке пространства ориентация пары векторов Е и Н в плоскости,
перпендикулярной лучу S, может изменяться со временем. В зависимости
от характера такого измерения различают естественный и поляризованный свет.
Обычные источники света являются совокупностью огромного
числа быстро высвечивающихся (10-7 — 10-8 с) элементарных источников
(атомов, молекул), испускающих свет независимо друг от друга, с различными фазами и разными ориентациями векторов Е и Н. Ориентации векторов Е и Н в результирующей волне хаотически изменяются во времени, так
что в плоскости, перпендикулярной к лучу S, все направления оказываются
равноправными. Такой свет называют естественным.
Поляризованным называется свет, в котором направления колебаний светового вектора Е упорядочены каким-либо образом.
Рассмотрим два взаимно перпендикулярных электрических колебания, совершающихся вдоль осей X и Y и отличающихся по фазе на :
Еx = А1 соs t;
Еy = А2 соs (t + ).
Результирующая напряженность Е является векторной суммой Еx
и Еy (рис. 1).
62
Ey
E

Ex
Рис. 1
Рис. 2
Угол  между Еx и Еy определяется выражением:
Еy
А2 соs (t + )
tg  = —— = ——————— .
Еx
А1 соs t
(1)
Если разность фаз s претерпевает случайные хаотические изменения, то и угол , т. е. направление светового вектора Е, будет испытывать скачкообразные изменения. В соответствии с этим естественный
свет можно представить как наложение двух некогерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях
и имеющих одинаковую интенсивность. Такое представление намного
упрощает рассмотрение прохождения естественного света через поляризационные устройства.
Пусть Еx и Еy когерентны, причем  равно нулю или , тогда;
А2
tg  =  —— = const ,
А1
(2)
т. е., результирующее колебание совершается в фиксированном направлении — волна плоскополяризована (рис. 2)
Когда А1 =А2 и  =  /2, тогда:
tg  =  tg t .
(3)
Отсюда вытекает, что плоскость колебаний поворачивается вокруг направления луча с угловой скоростью, равной частоте колебаний .
Свет в этом случае будет поляризованным по кругу (рис. 3).


Рис. 3
Рис. 4
63
Так как два взаимно перпендикулярных гармонических колебания одинаковой частоты при сложении дают в общем случае движение по
эллипсу, то при  = /2 и А1  А2 получим эллиптически поляризованную волну. Таким образом, точка с координатами Е x и Еy, то есть конец
вектора Е, движется по эллипсу. Следовательно, две когерентные плоскополяризованные волны, плоскости колебаний которых взаимно перпендикулярны, при наложении дают эллиптически-поляризованную световую волну (рис. 4).
При  = 0 или  эллипс вырождается в прямую и получается плоскополяризованный свет. При  =  /2 и А1 =А2 эллипс превращается в
окружность, получается свет, поляризованный по кругу (рис. 2, 3, 4).
В зависимости от направления вращения Е различают правую и
левую эллиптическую поляризацию.
Если по отношению к направлению, противоположному направлению луча, Е вращается по часовой стрелке, поляризация правая, иначе
— левая.
Плоскость, в которой колеблется световой вектор в плоскополяризованной волне, называется плоскостью колебаний.
Плоскость перпендикулярная плоскости колебаний называется
плоскостью поляризации.
Плоскополяризованный свет можно получить из естественного
света с помощью приборов, называемых поляризаторами. Эти приборы
свободно пропускают колебания параллельные плоскости, которую называют плоскостью поляризатора, и полностью или частично задерживают
колебания, перпендикулярные этой плоскости.
Поляризатор, задерживающий перпендикулярные к его плоскости колебания частично, называют несовершенным. Просто поляризатором мы будем для краткости называть идеальный поляризатор, полностью задерживающий колебания, перпендикулярные к его плоскости, и не
ослабляющий колебаний параллельных плоскости.
Всякий поляризатор может быть использован для исследования
поляризованного света, то есть в качестве анализатора.
Если на пути плоскополяризованного света поставить анализатор, то
интенсивность луча, прошедшего через анализатор, зависит от угла поворота
анализатора вокруг оси, совпадающей с направлением луча.
Колебания амплитуды А, совершающиеся в плоскости, образующей с плоскостью поляризатора угол , можно разложить на два колебания с амплитудами А = А cos  и А = А sin  (рис. 5).
64
A
A

A
Рис. 5
Первое колебание А пройдет через прибор, второе А будет задержано. Интенсивность прошедшей волны пропорциональна А2= A2 cos2, то
есть, равна I cos2, где I — интенсивность колебаний с амплитудой А,
падающей на прибор плоскополяризованной волны.
В естественном свете все значения  равновероятны. Поэтому доля естественного света, прошедшего через поляризатор, будет равна среднему
значению cos2, т. е. 1/2.
При вращении поляризатора вокруг направления естественного
луча интенсивность прошедшего света остается постоянной, изменяется
лишь ориентация плоскости колебаний света, выходящего из прибора.
Пусть на анализатор падает плоскополяризованный свет амплитуды А и интенсивности I. Сквозь анализатор пройдет лишь составляющая с амплитудой А=А0 cos , где  — угол между плоскостью колебаний
падающего света и плоскостью анализатора (рис. 6).
Следовательно, интенсивность прошедшего света I определяется
выражением:
I = I0 cos2 ,
(4)
2
2
(т. к. I ~ А и I0 ~ А0 ). Соотношение (4) носит название закона Малюса.
Таким образом, максимальная интенсивность света, вышедшего
из анализатора, получается при  = 0 (плоскости поляризатора и анализатора параллельны) и равна I=I0. При  = /2 I=0 — скрещенные поляризатор и анализатор света не пропускают.
3. Описание установки
Схема экспериментальной установки для проверки закона Малюса изображена на рис. 6.
Пучок световых лучей, получаемых с помощью осветителя S,
пройдя через диафрагму Д и систему поляризатор-анализатор Р—А, попадают на фотоэлемент.
65
Для объективных количественных измерений интенсивности
света применен селеновый фотоэлемент с запирающим слоем, представляющим собой железную пластинку с нанесенным на нее тонким слоем
селена.
S
Д
Р
А
A
шкала угла 
Рис. 6
При замкнутой цепи фотоэлемента фотоэлектроны, вырванные
светом из селена, будут двигаться в одну сторону, т. к. при движении в
противоположную сторону слой представляет для них гораздо большее
сопротивление. Величина фототока измеряется микроамперметром А
пропорционально интенсивности падающего на фотоэлемент света (первый закон фотоэффекта).
Измерение интенсивности света, прошедшего через анализатор,
производится для трех различных положений источника света S.
4. Порядок выполнения работы
1). Установить осветитель S вплотную к поляризатору Р. Установить поляризатор Р в положение  = 0. В этом случае стрелка микроамперметра должна отклоняться на максимальный угол, тогда I=I0.
2). Поворачивая поляризатор на различные углы от 0 o до 90 o
через 10, записываем показания микроамперметра. Данные заносим в
таблицу. Интенсивность света считаем в условных единицах по показаниям микроамперметра.
3). Рассчитать теоретическое значение интенсивности по закону
Малюса, считая I0 = Iпр (0). Данные занести в таблицу.
4). Построить график экспериментальной зависимости Iпр = f().
На том же чертеже аналогичным образом построить теоретическую зависимость Iт = f().
66
5). Отодвинуть осветитель S от поляризатора Р на большее расстояние и проделать пункты 2—4. Опыт повторить еще один раз.
Таблица
0
cos2
1- е положение
осветителя
Iпр
Iт
2– е положение
осветителя
Iпр
Iт
условные
единицы
3- е положение
осветителя
Iпр
Iт
0
10
20
30
40
50
60
70
80
90
5. Контрольные вопросы
1. Почему обычные источники не испускают поляризованный свет?
2. Какова структура естественного света?
3. При каком условии можно получить поляризованную волну?
Какие виды поляризации выделяют и чем они отличаются?
4. Может ли наблюдаться поляризация продольных волн?
5. Что такое плоскость поляризации?
6. Что такое плоскость колебаний?
7. Как получают поляризованный свет? Что такое поляризатор?
8. Для чего предназначен анализатор?
9. Выведите и объясните закон Малюса.
10. Как меняется интенсивность естественного света после прохождения через поляризатор? Почему?
11. Как зависит величина фототока от интенсивности света, падающего на фотоэлемент?
6. Литература
1. Савельев И. В. Курс общей физики. В 3-х т. Т. 2. — М.: Наука, 1978.
2. Яворский Б. М., Детлаф А. А., Курс физики. В 3-х т. Т. 3. — М.: Высшая
школа.
67