ЗАДАЧА 01

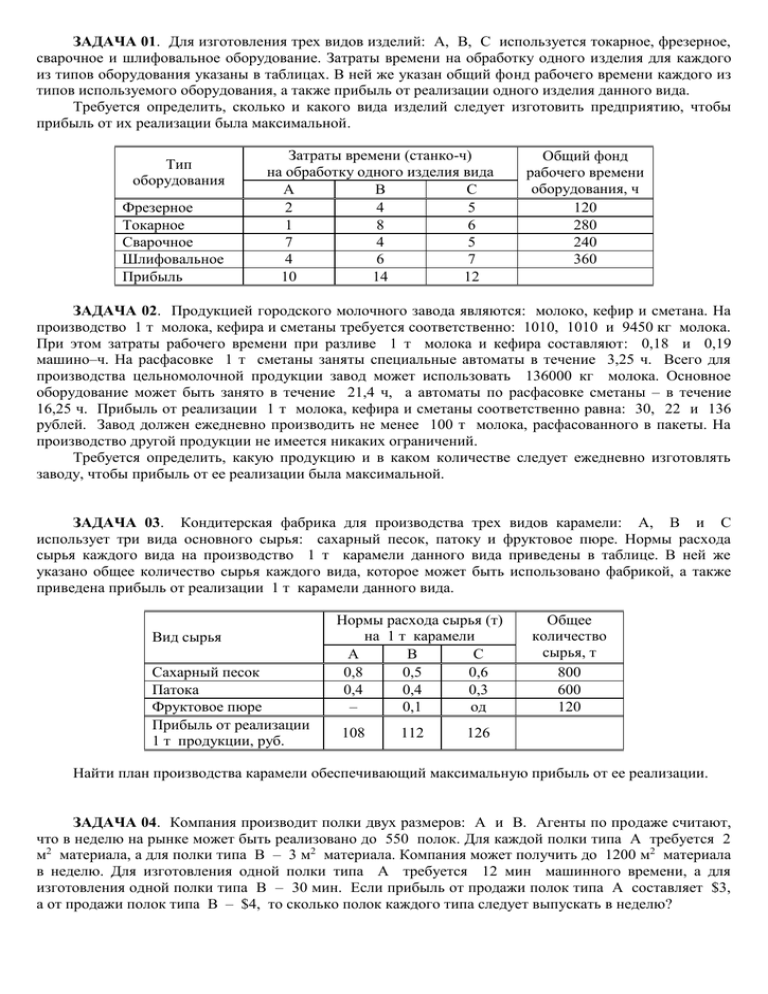
ЗАДАЧА 01. Для изготовления трех видов изделий: А, В, С используется токарное, фрезерное,
сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого
из типов оборудования указаны в таблицах. В ней же указан общий фонд рабочего времени каждого из
типов используемого оборудования, а также прибыль от реализации одного изделия данного вида.
Требуется определить, сколько и какого вида изделий следует изготовить предприятию, чтобы
прибыль от их реализации была максимальной.
Тип
оборудования
Фрезерное
Токарное
Сварочное
Шлифовальное
Прибыль
Затраты времени (станко-ч)
на обработку одного изделия вида
А
В
С
2
4
5
1
8
6
7
4
5
4
6
7
10
14
12
Общий фонд
рабочего времени
оборудования, ч
120
280
240
360
ЗАДАЧА 02. Продукцией городского молочного завода являются: молоко, кефир и сметана. На
производство 1 т молока, кефира и сметаны требуется соответственно: 1010, 1010 и 9450 кг молока.
При этом затраты рабочего времени при разливе 1 т молока и кефира составляют: 0,18 и 0,19
машино–ч. На расфасовке 1 т сметаны заняты специальные автоматы в течение 3,25 ч. Всего для
производства цельномолочной продукции завод может использовать 136000 кг молока. Основное
оборудование может быть занято в течение 21,4 ч, а автоматы по расфасовке сметаны – в течение
16,25 ч. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна: 30, 22 и 136
рублей. Завод должен ежедневно производить не менее 100 т молока, расфасованного в пакеты. На
производство другой продукции не имеется никаких ограничений.
Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять
заводу, чтобы прибыль от ее реализации была максимальной.
ЗАДАЧА 03. Кондитерская фабрика для производства трех видов карамели: А, В и С
использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода
сырья каждого вида на производство 1 т карамели данного вида приведены в таблице. В ней же
указано общее количество сырья каждого вида, которое может быть использовано фабрикой, а также
приведена прибыль от реализации 1 т карамели данного вида.
Вид сырья
Сахарный песок
Патока
Фруктовое пюре
Прибыль от реализации
1 т продукции, руб.
Нормы расхода сырья (т)
на 1 т карамели
A
В
С
0,8
0,5
0,6
0,4
0,4
0,3
–
0,1
од
108
112
Общее
количество
сырья, т
800
600
120
126
Найти план производства карамели обеспечивающий максимальную прибыль от ее реализации.
ЗАДАЧА 04. Компания производит полки двух размеров: А и В. Агенты по продаже считают,
что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2
м2 материала, а для полки типа В – 3 м2 материала. Компания может получить до 1200 м2 материала
в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для
изготовления одной полки типа В – 30 мин. Если прибыль oт продажи полок типа А составляет $3,
а от продажи полок типа B – $4, то сколько полок каждого типа следует выпускать в неделю?
ЗАДАЧА 05. Автозавод выпускает две модели: "Каприз" и "Фиаско". На заводе работает 1000
неквалифицированных и 800 квалифицированных рабочих, каждому из которых оплачивается 40 ч в
неделю. Для изготовления модели "Каприз" требуется 30 ч неквалифицированного и 50 ч
квалифицированного труда; для "Фиаско" требуется 40 ч неквалифицированного и 20 ч
квалифицированного труда. Каждая модель "Фиаско" требует затрат в размере $500 на сырье и
комплектующие изделия, тогда как каждая модель "Каприз" требует затрат в размере $1500;
суммарные затраты не должны превосходить $900 000 в неделю. Рабочие, осуществляющие доставку,
работают по пять дней в неделю и могут забрать с завода не более 210 машин в день.
Каждая модель "Каприз" приносит фирме $1000 прибыли, а каждая модель "Фиаско" – $500.
Какой объем выпуска каждой модели вы бы порекомендовали? Что бы вы порекомендовали для
повышения прибыли фирмы?
ЗАДАЧА 06. Заводы фирмы, расположенные в городах: Лидсе и Кардиффе, выпускают в год 800
и 500 т соответственно. Товары доставляются на склады городов: Манчестер, Бирмингем и Лондон,
которые вмещают: 400, 600 и 300 т соответственно.
Расстояния между этими городами приведены в таблице:
Лидс
Кардифф
Манчестер
40
170
Бирмингем
110
100
Лондон
190
150
Как следует транспонировать товары для минимизации расходов на перевозки, если стоимость
тонно-километра по любому маршруту составляет $2.
ЗАДАЧА 07. Фирма занимается составлением диеты, содержащей, по крайней мере, 20 единиц
белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь
этого при указанных в таблице ценах на 1 кг (или 1 л) пяти имеющихся продуктов?
Белки
Углеводы
Жиры
Витамины
Цена
Хлеб
Соя
2
12
1
2
12
12
0
8
2
36
Сушеная
рыба
10
0
3
4
32
Фрукты
Молоко
1
4
0
6
18
2"
3
4
2
10
ЗАДАЧА 08. Небольшая фирма производит два вида продукции, столы и стулья. Для
изготовления одного стула требуется 3 фута древесины, а для изготовления одного стола – 7 футов.
На изготовление одного стула уходит 2 ч рабочего времени, а на изготовление стола – 8 ч. Каждый
стул приносит $1 прибыли, а каждый стол – $3. Сколько стульев и сколько столов должна изготовить
эта фирма, если она располагает 420 футами древесины и 400 ч рабочего времени и хочет получить
максимальную прибыль?
ЗАДАЧА 09. У фермера есть 400 акров земли, на которой он планирует посеять зерно и соевые
бобы. Засеять каждый акр зерна и собрать с него урожай стоит $200, а засеять и собрать урожай с
каждого акра соевых бобов – $100. Фермер получил заем в $60 000 долларов для того, чтобы покрыть
затраты. Каждый акр зерна принесет 30 бушелей зерна, а каждый акр соевых бобов – 60 бушелей.
Фермер обязался продавать зерно и соевые бобы по $3 и по $6 за бушель, соответственно. Однако
фермеру нужно хранить в амбаре зерно и соевые бобы в течение нескольких месяцев после сбора
урожая. Максимальная вместимость амбара составляет 21 000 бушелей.
Сколько акров каждой культуры нужно засеять, чтобы прибыль была наибольшей?
2
ЗАДАЧА 10. Фирма, изготовляющая деревянную продукцию, производит два вида обшивочных
панелей: колониальную и западную. Производство, панелей осуществляется двумя операциями:
прессованием и отделкой. Задача администрации фирмы – узнать, сколько пластов обоих типов
обшивочной панели нужно производить в месяц, чтобы получить максимальную прибыль.
Фирма получает $80 прибыли за каждые 100 пластов колониальной панели и $100 – за каждые
100 пластов западной панели.
Ресурсные потребности и возможности для каждого типа панелей, которые образовывают
параметры модели, приведены в таблице:
Средства
Деревянная продукция
Прессование
Отделка
Стоимость
Необходимые средства для партии
из 100 пластов обшивочной панели
Колониальные
Западные
20 кг
40 кг
4ч
6ч
4ч
4ч
$30
$50
Всего средств
в месяц
4000 кг
900 ч
600 ч
$6000
ЗАДАЧА 11. В трех пунктах отправления: А1, А2 и А3 сосредоточен однородный груз в
количествах, равных: 420, 380 и 400 т. Этот груз необходимо перевезти в три пункта назначения: B1,
B2 и B3 в количествах, соответственно равных: 260, 520 и 420 т. Долларовые тарифы перевозок 1 т
груза из каждого пункта отправления в каждый пункт назначения являются известными величинами и
задаются таблицей:
В1
2
7
6
А1
А2
А2
В2
4
5
9
В2
3
8
7
Найти план перевозок, обеспечивающий вывоз имеющегося в пунктах отправления и завоз
необходимого в пунктах назначения груза при минимальной общей стоимости перевозок.
ЗАДАЧА 12. Четыре предприятия: B1, B2, B3 и B4 для производства продукции используют
три вида сырья: А1, А2 и А3. Потребности в сырье каждого из предприятий соответственно равны:
120, 50, 190 и 110 единиц. Сырье сосредоточено в трех местах его получения, а запасы
соответственно равны: 160, 140 и 170 единиц. На каждое из предприятий сырье может завозиться из
любого пункта его получения. Тарифы перевозок являются известными величинами и задаются
таблицей:
А1
А2
А2
В1
7
4
9
В2
8
5
2
В3
1
9
3
В4
2
8
6
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.
ЗАДАЧА 13. На трех складах: А1, А2 и А3 оптовой базы сосредоточен однородный груз в
количествах: 90, 60 и 150 единиц. Этот груз необходимо перевезти в четыре магазина: B1, B2, B3 и
B4. Каждый из магазинов должен получить соответственно: 120, 40, 60 и 80 единиц груза. Тарифы
перевозок единицы груза из каждого склада во все магазины задаются таблицей:
3
В1
2
5
2
А1
А2
А2
В2
3
3
1
В3
4
1
4
В4
3
2
2
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.
ЗАДАЧА 14. Производственное объединение имеет в своем составе три филиала: А1, А2 и А3,
которые производят однородную продукцию соответственно в количествах, равных: 50, 30 и 10
единиц. Эту продукцию получают четыре потребителя: B1, B2, B3 и B4, расположенные в разных
местах. Их потребности соответственно равны: 30, 30, 10 и 20 единиц. Тарифы перевозок единицы
продукции от каждого из филиалов до любого из потребителей задаются таблицей:
В1
1
2
3
А1
А2
А2
В2
2
3
2
В3
4
1
4
В4
1
5
4
Составить такой план прикрепления получателей продукции к ее поставщикам, при котором
общая стоимость перевозок является минимальной.
ЗАДАЧА 15. Три предприятия: А1, А2 и А3 могут производить некоторую однородную
продукцию в количествах, соответственно равных: 180, 350 и 20 единиц. Эта продукция должна быть
поставлена пяти потребителям: B1, B2, B3, B4 и B5 в количествах, соответственно равных: 110, 90,
120, 80 и 150 единиц. Затраты, связанные с доставкой единицы продукции, задаются таблицей:
В1
7
1
6
А1
А2
А2
В2
12
8
13
В3
4
6
8
В4
6
5
7
В5
5
3
4
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.
ЗАДАЧА 16. Для строительства четырех дорог: B1, B2, B3 и B4 используется гравий из трех
карьеров: А1, А2 и А3. Запасы гравия в каждом из карьеров соответственно равны: 120, 280 и 160
единиц. Потребности в гравии для строительства каждой из дорог соответственно равны: 130, 220, 60
и 70 единиц. Известны также тарифы перевозок 1 единицы гравия из каждого карьера к каждой из
строящихся дорог, которые задаются таблицей:
А1
А2
А2
В1
1
4
3
В2
7
2
8
В3
9
6
1
В4
5
8
2
Составить такой план перевозок гравия, при котором потребности в нем каждой из строящихся
дорог были бы удовлетворены при наименьшей общей стоимости перевозок.
ЗАДАЧА 17. Для строительства четырех объектов: B1, B2, B3 и B4 используется кирпич,
изготовляемый на трех заводах: А1, А2 и А3. Ежедневно каждый из заводов может изготовлять: 100,
150 и 50 единиц кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов
4
равны: 75, 80, 60 и 85 единиц. Известны также тарифы перевозок 1 единицы кирпича с каждого
завода к каждому из строящихся объектов:
А1
А2
А2
В1
6
1
8
В2
7
2
10
В3
3
5
20
В4
5
6
1
Составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость
перевозок является минимальной.
ЗАДАЧА 18. На трех мукомольных комбинатах: А1, А2 и А3 ежедневно производится: 110,
190 и 90 т муки. Эта мука потребляется четырьмя хлебозаводами: B1, B2, B3 и B4, потребности
которых равны соответственно: 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с мукомольных
комбинатов к каждому из хлебозаводов задаются таблицей:
А1
А2
А2
В1
6
1
8
В2
7
2
10
В3
3
5
20
В4
5
6
1
Составить такой план доставки муки, при котором общая стоимость перевозок является
минимальной.
ЗАДАЧА 19. В трех хранилищах горючего: А1, А2 и А3 ежедневно хранится: 175, 125 и 140
т бензина. Этот бензин ежедневно получают четыре заправочные станции: B1, B2, B3 и B4 в
количествах, равных соответственно: 180, 110, 60 и 40 т. Тарифы перевозок 1 т бензина от
хранилищ к заправочным станциям задаются таблицей:
А1
А2
А2
В1
9
1
3
В2
7
2
5
В3
5
4
8
В4
3
6
9
Составить такой план перевозок бензина, при котором общая стоимость перевозок является
минимальной.
ЗАДАЧА 20. Компания имеет два товарных склада: А1 и А2, а также и трех оптовых
покупателей: В1, В2 и В3. Известно, что общий объем запасов на складах составляет 300 000 единиц
продукции и совпадает с общим объемом заказов покупателей. Конкретные данные о загруженности
каждого из складов, потребности каждого покупателя и стоимости перевозки приведены в таблице:
Склады
А1
А2
Запрос
Стоимость перевозок от склада
к потребителям, руб./единица
В1
В2
В3
8
5
6
4
9
7
70 000
140 000
90 000
Наличие
120 000
180 000
300 000
Минимизируйте общую стоимость перевозок.
5
ЗАДАЧА 21. Два торговых склада: А1 и А2 поставляют продукцию в четыре магазина: В1,
В2, В3 и В4. Издержки транспортировки продукции с торговых складов в магазины, а также наличие
продукции на складах и объемы ее магазинами приведены в таблице:
Стоимость перевозок от склада
к магазинам, руб./единица
В1
В2
В3
В4
4
3
5
6
8
2
4
7
50
100
75
75
Склады
А1
А2
Запрос
Наличие
100
200
300
Минимизируйте общую стоимость перевозок.
ЗАДАЧА 22. Предположим, что нужно перевезти весь груз с трех складов: А1, А2 и А3 в два
пункта: В1 и В2, причем весь груз должен быть перевезен во все пункты. В первый пункт должно
быть перевезено 45 единиц груза, во второй – 79. На складах груз распределен следующим образом:
на первом – 18, на втором – 75, на третьем – 31. Стоимость перевозки единицы груза со склада в
пункт назначения приведена в таблице:
В1
17
12
9
А1
А2
А2
В2
6
13
8
Требуется так организовать перевозку грузов, чтобы транспортные затраты были минимальными.
ЗАДАЧА 23. Задача о расписании полетов
Ежедневно некоторая авиалиния осуществляет следующие перелеты между городами X и Y:
№ полета
1
2
3
4
5
Отправление из X
09:00
10:00
15:00
19:00
20:00
Прибытие в Y
11:00
12:00
17:00
21:00
22:00
№ полета
11
12
13
14
15
Отправление из Y
08:00
09:00
14:00
20:00
21:00
Прибытие в X
10:00
11:00
16:00
22:00
23:00
Требуется:
• Организовать полеты "туда" и "обратно" так, чтобы минимизировать время простоя при условии,
что каждому самолету требуется, по крайней мере, 1 ч для заправки;
• Составить расписание полетов, совершаемых каждым из самолетов;
• Представить найденное решение в виде диаграммы;
• Выяснить сколько самолетов требуется для полетов по составленному расписанию.
Методические указания к решению
1. Вычислим по расписанию перелетов время простоя в каждом случае и запишем результат в
таблицу:
Полет
вX
11
12
13
1
2
3
4
5
23
22
17
24
23
18
5
4
23
9
8
3
10
9
9
Полет
вY
1
2
3
11
12
13
14
15
21
20
15
22
21
16
3
2
21
9
8
3
10
9
4
6
14
15
11
10
12
11
17
16
21
20
22
21
4
5
11
10
12
11
17
16
23
22
24
23
2. Составим задачу целочисленного программирования о минимизации времени простоя и решим
ее средствами MS Excel (аналогично решению Задания 8).
3. Выясним по схеме полетов минимальное число самолетов, необходимых для организации
перелетов.
Литература
1. Андрияшин Х.А., Казанцев С.Я. и др. Информатика и математика для юристов. – М.: ЮНИ
ТИ, 2002.
2. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа,
1993.
7