Пакет статистической обработки экспериментальных данных

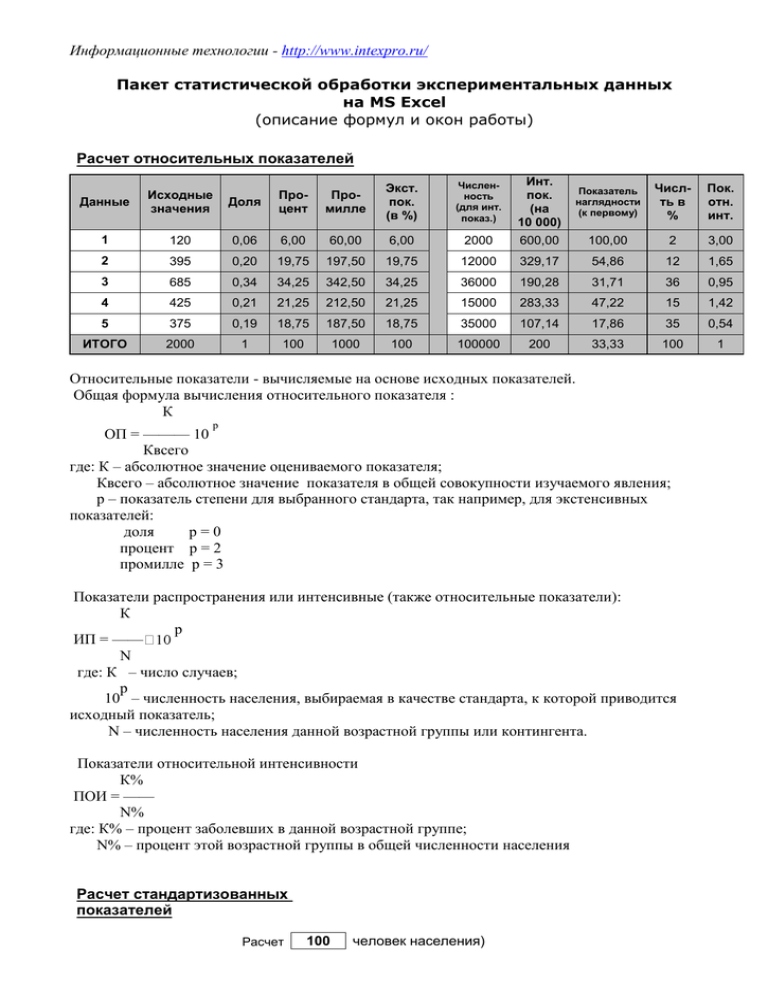
Информационные технологии - http://www.intexpro.ru/
Пакет статистической обработки экспериментальных данных
на MS Excel
(описание формул и окон работы)
Расчет относительных показателей
Доля
Процент
Промилле
Экст.
пок.
(в %)
Численность
(для инт.
показ.)
Инт.
пок.
(на
10 000)
Показатель
наглядности
(к первому)
Числть в
%
Пок.
отн.
инт.
120
0,06
6,00
60,00
6,00
2000
600,00
100,00
2
3,00
2
395
0,20
19,75
197,50
19,75
12000
329,17
54,86
12
1,65
3
685
0,34
34,25
342,50
34,25
36000
190,28
31,71
36
0,95
4
425
0,21
21,25
212,50
21,25
15000
283,33
47,22
15
1,42
5
375
0,19
18,75
187,50
18,75
35000
107,14
17,86
35
0,54
ИТОГО
2000
1
100
1000
100
100000
200
33,33
100
1
Данные
Исходные
значения
1
Относительные показатели - вычисляемые на основе исходных показателей.
Общая формула вычисления относительного показателя :
К
p
ОП = ——— 10
Квсего
где: К – абсолютное значение оцениваемого показателя;
Квсего – абсолютное значение показателя в общей совокупности изучаемого явления;
p – показатель степени для выбранного стандарта, так например, для экстенсивных
показателей:
доля
p=0
процент p = 2
промилле p = 3
Показатели распространения или интенсивные (также относительные показатели):
К
p
ИП = ——
N
где: К – число случаев;
p
10 – численность населения, выбираемая в качестве стандарта, к которой приводится
исходный показатель;
N – численность населения данной возрастной группы или контингента.
Показатели относительной интенсивности
К%
ПОИ = ——
N%
где: К% – процент заболевших в данной возрастной группе;
N% – процент этой возрастной группы в общей численности населения
Расчет стандартизованных
показателей
Расчет
100
человек населения)
(на
Расчет стандартизованных показателей (Прямой
метод расчета)
групппы
населения
Первые данные (ПД)
Численность
Колво
случаев
1
2
3
95
22
158
79
5
14
Итого
275
98
Вторые данные (ВД)
Показатель
Числен
-ность
Колво
случаев
83,16
22,73
8,86
35,64
137
45
497
108
19
57
679
184
Показатель
78,83
42,22
11,47
27,10
Общая
численность
(сумма)
Стандарт
численности
232
67
655
954
24,32
7,02
68,66
100
Стандартизованны
е показатели
ПД
ВД
20,22
1,60
6,08
19,170913
2,9652923
7,8742898
27,90
30,01
Стандартизованные показатели
Общая формула прямого метода вычисления:
Ki
СП = ∑ —— ∙ Nстi
Ni
где: Ki – исходный показатель населения;
Ni – численность населения i-й группы;
Nстi – численость населения i-й группы в принятом за основу стандарте, например на 1000
или 100000 тыс. населения
В качестве стандарта распределения населения по группам могут быть взяты, например, средние
данные по всем сравниваемым территориям или другие стандарты в зависимости от целей
исследования.
Расчет показателей распределения
№ п/п
Исходные
значения
Ранг
Средняя
Медиана
1
2
3
4
5
6
7
8
9
10
13
73
7
102
54
96
21
63
77
92
2
6
1
10
4
9
3
5
7
8
59,80
68,00
Сумма
598
Отклонение
Стандартное
отклонение
Коэффициент
вариации
(%)
Амплитуда
-46,80
13,20
-52,80
42,20
-5,80
36,20
-38,80
3,20
17,20
32,20
35,16
58,79
95,00
0,00
Статистические показатели распределения - показатели, характеризующие совокупность
исходных наблюдений (показателей).
Выборочная средняя (арифметическая):
Хi
М = ∑ ——
n
где: Хi – одно из значений показателя (i = 1, …, n);
n – общее количество наблюдений
Медиана (Ме) - величина, делящая вариационный ряд пополам
Стандартная ошибка или среднее квадратичное отклонение (равная корню квадратному из
дисперсии):
σ(Х) =
√ ∑ (Хi – М)2 / (n -1)
Коэффициент вариации:
σ(Х)
К = ——— ∙ 100
М
Амплитуда - разница между крайними значениями
Оценка достоверности показателей
Вычисление средних значений
Вычисление долей
Превышение норматива: "Норма" =
Исходные значения
№
п/п
Данные
1
Отклонение от М
Данные
2
Отклонение от М
№
п/п
Прев. даными 1
"нормы"
Прев. даными 2
"нормы"
1
2
3
4
5
6
7
8
9
10
37
21
19
63
122
87
29
30
52
17
-10,7
-26,7
-28,7
15,3
74,3
39,3
-18,7
-17,7
4,3
-30,7
44
63
89
130
98
74
49
62
26
45
-24,0
-5,0
21,0
62,0
30,0
6,0
-19,0
-6,0
-42,0
-23,0
1
2
3
4
5
6
7
8
9
10
нет
нет
нет
Да
Да
Да
нет
нет
нет
нет
нет
Да
Да
Да
Да
Да
нет
Да
нет
нет
Среднее
(М)
Ошибка
значений
1
Среднее
(М)
Ошибка
значений
2
Доля "Да"
(R%)
Доля "Да"
(R%)
30
60
34,28
Ошибка
среднего
Ошибка доли
Ошибка доли
15,28
16,33
47,7
Ошибка
среднего
10,84
68
30,75
Результат
9,73
60
Результат
Суммарная ошибка среднего =
14,56
Суммарная ошибка среднего =
22,36
Значение t-критерия (для оценки
достоверности отличия средних) =
1,39
Значение t-критерия (для оценки
достоверности отличия долей) =
1,34
Оценка достоверности показателей – степень точности выборочного наблюдения
характеризуется соответствующей ошибкой (называемой иногда, ошибкой репрезентативности),
которая представляет собой разность между рассчитанным значением показателя и его истинным
значением
Ошибка выборочного среднего М вычисляется по формуле:
σ(Х)
σ(М) = ——
√n
где: σ(Х) – ошибка исходных наблюдений Хi (среднее квадратичное отклонение),
n – численность выборки
Ошибка для доли Р (процента, промилле и др.) при альтернативной вариации данных
- при количестве наблюдений более 30: σ(R) = √ R ∙ Q / n
- при количестве наблюдений менее 30: σ(R) =
Х
где: R = ———— ∙ 10
Хвсего
p
√R∙Q
/ (n - 1)
(p – выбранный показатель стандарта),
p
Q = (10 – R)
n – число наблюдений.
Разброс значений исходного показателя Х:
для выборочного среднего:
М± = М ± σ(М) ∙ tα
для доли (процента и так далее): R± = R ± σ(R) ∙ tα
где: tα- значение распределения Стьюдента для выбранной доверительной вероятности α при (n боды
Оценка достоверности разности двух показателей (Р1 и Р2) описывается t-распределением
Стьюдента с числом степеней свободы n = n1 + n2 – 2:
t = (Р1 – Р2) / σ1, 2
где: σ1, 2 =
√ σ1
2
2
+ σ 2 - суммарная ошибка двух показателей
Исключение аномальных значений
№ п/п
Исходный
значения
Параметрический
критерий
Непараметрический критерий
Отклонение от
М
V
Ранг
1
2
3
4
5
6
7
8
9
37
21
19
63
122
87
29
30
52
-10,70
-26,70
-28,70
15,30
74,30
39,30
-18,70
-17,70
4,30
-0,31
-0,78
-0,84
0,45
2,17
1,15
-0,55
-0,52
0,13
6
3
2
8
10
9
4
5
7
10
17
-30,70
1
Всего
10
Среднее (М)
Ошибка
значений
-0,90
Мин Макс
V
V
47,7
34,28
-0,90
r
Для
макс.
Для мин.
r10
0,33
0,02
r11
0,34
0,03
r20
0,57
0,06
r21
0,58
0,09
2,17
Исключение аномальных значений - аномальными считаются те значения из анализируемой
совокупности, которые не укладываются в имеющуюся закономерность, то есть резко
выделяются
Параметрический метод исключения аномальных значений - при известных параметрах
распределения М и σ(Х) :
1) Вычисление статистики V
| Хi – М |
V = макс ————
σ(Х)
2) Сравнение V с критическим значением Vα, зависящим от числа степеней свободы (n - 1) и
принятой доверительной вероятности α (обычно выбирается α > 0,95). Аномальным считается
значение, удовлетворяющее условию:
V > Vα
3) Повторение процедуры вычислений для оставшихся n = n –1 значений до тех пор, пока
последнее условие не будет выполнено
Непараметрический метод исключения аномальных значений – как правило при n < 25:
1) Ранжирование анализируемых значений Х1 ≤ Х2 ≤ ... ≤ Хn
2) Вычисление статистики r для крайних значений:
При проверке максимального значения Хn
- число значений: 3 ≤ n ≤ 7 : r10 = (Хn – Хn-1) / (Хn – Х1)
- число значений: 8 ≤ n ≤ 10 : r11 = (Хn – Хn-1) / (Хn – Х2)
- число значений: 11 ≤ n ≤ 13 : r20 = (Хn – Хn-2) / (Хn – Х2)
- число значений: 14 ≤ n
: r21 = (Хn – Хn-2) / (Хn – Х3)
При проверке минимального значения Х1
- число значений: 3 ≤ n ≤ 7 : r10 = (Х2 – Х1) / (Хn – Х1)
- число значений: 8 ≤ n ≤ 10 : r11 = (Х2 – Х1) / (Хn-1 – Х1)
- число значений: 11 ≤ n ≤ 13 : r20 = (Х3 – Х1) / (Хn-1 – Х1)
- число значений: 14 ≤ n
: r21 = (Х3 – Х1) / (Хn-2 – Х1)
3) Полученное значение r сравнивается с критическим rα и считается аномальным, если:
r > rα
4) Процедура проверки повторяется для оставшихся n –1 значений
Расчет показателей динамического ряда
t
Уt
Уср.
(средний
уровень)
1
2
3
4
5
6
7
8
9
10
11
376
109
289
278
401
295
80
123
482
305
209
254,33
254,33
254,33
254,33
254,33
254,33
254,33
254,33
254,33
254,33
254,33
ПАt
(абсолютный
прирост)
ПО
(общий
абс.
прирост)
ТРt
(темп
роста)
ТПt
(темп прироста)
-271,00
-267,00
180,00
-11,00
123,00
-106,00
-215,00
43,00
359,00
-177,00
-96,00
28,99
265,14
96,19
144,24
73,57
27,12
153,75
391,87
63,28
68,52
-71,01
165,14
-3,81
44,24
-26,43
-72,88
53,75
291,87
-36,72
-31,48
СТРt
(средний
темп
роста)
СТПt
(средний
темп прироста)
89,05
-10,95
12
105
254,33
-104,00
50,24
-49,76
Основные параметры динамического ряда
Уровни ряда (Уt) – конкретные его значения во времени
Средний уровень ряда:
Уср = (∑ Уt) / n
где: Уt – уровни ряда; n – число членов ряда (t = 1,…, n)
Абсолютный прирост (снижение) :
ПА t = Уt - Уt-1
Общий абсолютный прирост :
ПО = ∑ Па = ∑ (Уt - Уt-1) = Уn - У1
Темп роста (снижения):
ТР t = (Уt / УtТемп прироста (убыли):
ТП t = (ПА t / Уt-1)
∙
100 = ТР t – 100
Средний темпа роста:
СТРср = n-1√
Средний темп прироста:
СТПср = СТРср – 100
Выравнивание динамического ряда
t
Уt
Уср
1
2
3
4
5
6
7
8
1
3
2
0
1
3
0
2
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
Сумма за 5
дн.
7,00
7,00
Групповая
средняя
(за 5
дн.)
1,4
1,4
1,4
1,4
1,4
1,4
1,4
1,4
Скользящая средняя
(за 5 дн.)
1,40
1,80
1,20
1,20
1,20
1,40
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
0
2
4
5
3
7
5
2
10
2
4
0
4
2
5
7
3
9
1
4
0
2
3
0
1
2
0
4
2
5
0
7
4
1
3
2
1
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
2,84
24,00
18,00
21,00
16,00
6,00
18,00
11,00
1,4
1,4
4,8
4,8
4,8
4,8
4,8
3,6
3,6
3,6
3,6
3,6
4,2
4,2
4,2
4,2
4,2
3,2
3,2
3,2
3,2
3,2
1,2
1,2
1,2
1,2
1,2
3,6
3,6
3,6
3,6
3,6
2,2
2,2
2,2
2,2
2,2
1,60
2,60
2,80
4,20
4,80
4,40
5,40
5,20
4,60
3,60
4,00
2,40
3,00
3,60
4,20
5,20
5,00
4,80
3,40
3,20
2,00
1,80
1,20
1,60
1,20
1,40
1,80
2,60
2,20
3,60
3,60
3,40
3,00
3,40
2,20
1,40
1,20
Выравнивание динамических рядов – применяется для выявления основной тенденции
Методы:
- увеличение интервала,
- вычисление групповой средней,
- вычисление скользящей средней,
- выравнивание по прямой и др.
Анализ сезонности
t
Уt
1
2
3
4
23
34
47
45
5
79
6
7
8
136
95
35
Уср. год
(среднемесячный
уровень)
ПСКt
(показатель
сезонных
колебаний)
45,17
66,78
92,31
88,38
155,16
9
50,92
ИС (индекс
сезонности)
Сумма за
месяцы
подъема
(ПСКt>100)
Сумма за
остальные
месяцы
(ПСКt<100)
КС (коэффициент
сезонности)
375
Сумма за
месяцы
подъема
(ПСКt>100)
375
236
Сумма за все
месяцы года
611
1,59
Коэффициен
т сезонности
61,37
Сумма за
месяцы
подъема
(ПСКt>100)
592
Сумма за
месяцы
подъема
(ПСКt>100)
592
Сумма за
остальные
месяцы
(ПСКt<100)
194
Сумма за все
месяцы года
786
Индекс
сезонности
3,05
Коэффициен
т сезонности
75,32
Сумма за
месяцы
подъема
(ПСКt>100)
457
Сумма за
месяцы
подъема
(ПСКt>100)
457
Сумма за
остальные
месяцы
(ПСКt<100)
454
Сумма за все
месяцы года
911
ПСП
(показатель
сезонного
подъема)
267,10
65
186,58
10
13
68,74
11
12
13
14
15
16
24
127,66
25,53
47,14
29,46
68,70
51,91
35,11
15
45
34
23
67
102,29
17
Индекс
сезонности
42,06
81
123,66
18
19
20
176
111
76
21
81
65,50
268,70
169,47
22
32
116,03
23
24
25
26
27
28
29
45
123,66
48,85
68,70
22,90
88,25
44,79
73,77
15
67
34
56
67
154
75,92
88,25
202,85
30
31
32
205
98
54
270,03
50,64
33
25
129,09
34
70
71,13
35
36
25
56
Индекс
сезонности
1,01
Коэффициен
т сезонности
33,55
50,16
32,93
92,21
32,93
73,77
Показатель сезонных колебаний:
ПСК t = (Уt / Среднемесячный уровень)
где: Уt – ежемесячные уровни ряда
t – месяцы,
Среднемесячный уровень = суммарный годовой уровень / 12
Индекс сезонности:
ИС = ∑ Уtп / ∑ Уtо
где: tп – месяцы подъема, для которых ежемесячные уровни больше среднемесячных,
tо – остальные месяцы
Коэффициент сезонности:
КС = (∑ Уtп / ∑ Уtг ) ∙
где: tп – месяцы подъема, для которых ежемесячные уровни больше среднемесячных,
tг – все месяцы года
Показатель сезонного подъема:
∑Уtг - ∑Уtп
∑ Уtп – ————— ∙ ∑tп
12 - ∑tп
ПСП = ———————————— ∙ 100
∑ Уtг
где: ∑Уtг – общее число заболеваний за год;
∑Уtп – число заболеваний в месяцы подъема;
∑ tп – число месяцев подъема.
Установление превышений текущего обычного уровня (подъемов)
Tб
7
Zв
1
Zн
3
t
Исходные
значения
Скользящее
среднее
Нормированный
показатель (НП)
Возможен
подъем
Начало
подъема
НП за
Т
Xt
Mt
Zt
tвн
tн
ZT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
1
3
2
0
1
3
0
2
0
2
4
5
3
7
5
2
10
2
4
0
4
2
5
7
3
9
1
4
0
2
3
0
1
1,00
1,00
1,29
1,39
1,19
1,16
1,42
1,22
1,33
1,14
1,26
1,66
2,13
2,26
2,93
3,23
3,05
4,05
3,75
3,79
3,25
3,36
3,16
3,42
3,94
3,80
4,54
4,04
4,03
3,46
3,25
3,21
2,75
0,00
2,16
0,65
-1,32
-0,17
1,82
-1,25
0,67
-1,20
0,76
2,51
2,41
0,50
2,89
0,92
-0,56
3,33
-0,66
0,08
-1,38
0,26
-0,51
0,73
1,48
-0,37
2,17
-1,24
-0,01
-1,49
-0,51
-0,09
-1,28
-0,68
0
2
2
0
0
6
0
0
0
0
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
0
0
0
0
0
0
0
0
0
0
0
0
0
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
0
0
0,00
2,16
1,88
0,74
0,00
1,82
0,27
0,00
0,00
0,00
2,51
3,44
2,80
3,93
3,69
2,89
4,05
3,05
2,74
1,98
1,93
1,66
1,80
2,14
1,95
2,44
1,97
1,89
1,44
1,26
1,20
0,90
0,00
Управляющие
параметры
Выявленные
подъемы
П
П
П
П
П
П
П
П
П
П
П
П
П
П
П
П
П
П
П
П
П
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
2
0
4
2
5
0
7
4
1
3
2
1
0
3
0
5
1
0
2
0
4
7
2
10
11
3
5
1
0
3
0
0
0
0
0
0
0
2,50
2,43
2,08
2,36
2,31
2,69
2,31
2,98
3,12
2,82
2,85
2,72
2,48
2,12
2,25
1,93
2,37
2,17
1,86
1,88
1,61
1,95
2,67
2,58
3,64
4,69
4,45
4,53
4,02
3,45
3,38
2,90
2,49
2,13
1,83
1,57
1,34
-0,20
-1,06
0,84
-0,16
1,31
-1,26
2,15
0,39
-0,87
0,08
-0,38
-0,84
-1,24
0,43
-1,17
1,58
-0,65
-1,09
0,07
-1,02
1,30
2,66
-0,27
3,20
2,19
-0,42
0,15
-1,00
-1,16
-0,13
-1,04
-0,89
-0,78
-0,70
-0,62
-0,56
-0,51
0
0
0
0
38
0
40
40
0
0
0
0
0
0
0
49
0
0
0
0
54
54
54
54
54
54
54
54
54
54
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
54
54
54
54
54
54
54
0
0
0
0
0
0
0
0,00
0,00
0,00
0,00
1,31
0,00
1,28
1,27
0,70
0,00
0,00
0,00
0,00
0,00
0,00
1,58
0,60
0,00
0,00
0,00
1,30
2,82
1,86
3,30
3,94
2,92
2,62
1,98
1,39
1,26
0,87
0,00
0,00
0,00
0,00
0,00
0,00
П
П
П
П
П
П
П
П
П
П
Оценка данных в сравнении с обычными уровнями позволяет выявить, тенденцию изменения
показателя и текущие отклонения от нее.
Тенденции связывают с долговременными факторами, влияющими на анализируемый
показатель.
Отклонения от тенденций – предмет оперативного вмешательства в ситуацию.
Оперативная оценка изменения уровня контролируемого процесса (КП), представляемого в виде
динамического ряда, выполняется в три этапа:
1) вычисление параметров текущего обычного уровня (ТОУ)
2) установление изменений
3) оценка степени изменений
1. Вычисление параметров ТОУ :
-текущее значение обычного уровня ТОУt по K прошлым (или одноименным) периодам
(интервалам времени) ряда (n = 1, N):
1 N
ТОУt = — ∑ Yt-n
N n=1
-дисперсия значений ряда относительно ТОУ:
1
N
Dt = —— ∑ (Yt-n – ТОУt )2
N – 1 n=1
2. Установление изменений выполняется путем оценки значимости отклонения фактически
наблюдаемых значений от ТОУ с помощью статистик:
Yt – ТОУt
Zt = —————
√ Dt
где: ТОУt и Dt - соответственно, значение текущего обычного уровня и
дисперсия значений ряда относительно ТОУt, с которым
выполняется сравнение;
и
YT – ТОУT
ZT = —————
√ DT
где: УT - сумма значений КП за период T = (t – tв +1), где tв – возможное
начало изменения, t - последний момент времени
ТОУT = ∑ ТОУt = T ∙ ТОУtв – текущий обычный уровень для периода T,
а ТОУtв – текущий обычный уровень на момент установления
возможного начала изменения;
DT - дисперсия отклонения от ТОУ для периода T.
3. Оценка степени изменений выполняется на основе статистики ZT, вычисленной для
суммарного с начала изменения tн уровня УT,
где T = (t – tн +1):
при ZT > Z2
- Очень значительное (очень большое)
при Z2 ≥ ZT > Z1 - Значительное (большое)
при Z1 ≥ ZT
- Незначительное (небольшое)
Расчет коэффициента корреляции рядов
Исходные
значения
ряда 1
(X)
Исходные
значения
ряда 2
(Y)
1
2
3
4
5
6
7
4
1
1
44
35
40
38
11,5
10,6
9,4
16,5
11,8
12,0
14,0
Количество
членов ряда
(n)
X
163
X - среднее
23,29
Y
85,8
Y - среднее
12,26
t
7
Отклонение
от средней
dx
dy
-19,29
-22,29
-22,29
20,71
11,71
16,71
14,71
-0,8
-1,7
-2,9
4,2
-0,5
-0,3
1,7
Коэффициент корреляции Rxy =
dx  dy
d2x
d2y
14,60
36,93
63,67
87,89
-5,36
-4,30
25,64
371,94
496,65
496,65
429,08
137,22
279,37
216,51
0,57
2,75
8,16
18,00
0,21
0,07
3,04
 (d x  d y )
219,09
219,09
Результаты
вычислений
 d2x
 d2y
2427,4
32,80
3 2x d2y)
d
282,16
/
282,16
Достоверность коэффициента корреляций mR =
0,78
0,15
В статистике сила и направленность корреляционной связи оценивается по коэффициенту
корреляции, величина которого изменяется от -1 до +1.
Обычно различают следующие степени корреляционной связи (по модулю – без знака):
1) корреляция слабая (низкая)
- Кк от 0,0 до 0,29
2) корреляция средняя
- Кк от 0,3 до 0,69
3) корреляция сильная (высокая) - Кк от 0,7 до 1,0
Коэффициент корреляции рядов применяется в случае, когда исходные данные представлены
двумя рядами величин, и вычисляется по формуле:
∑ (dx ∙ dy)
Rxy = ———————
√ ∑dx2 ∙ ∑dy2
где: X, Y – коррелируемые ряды
dx, dy – отклонения значений рядов X, Y от своих арифметических средних.
Достоверность коэффициента корреляции оценивается по средней ошибке, вычисляемой по
формуле:
mR = ± (1- Rxy2) / √ n
где: n - число членов сравниваемых рядов.
Значение коэффициента корреляции считается достоверным, если оно превышает свою среднюю
ошибку более чем в 3 раза.
Расчет коэффициента корреляции рангов
t
Исходные
значения
ряда 1
Исходные
значения
ряда 2
1
2
3
4
5
6
7
8
9
10
11
78
47
40
51
60
58
53
60
55
74
58
10,0
4,0
1,2
3,3
9,0
13,0
4,8
5,8
5,3
15,3
6,8
Количество
членов ряда
(n)
11

Ранги
Ряда
1
Ряда
2
(X)
(Y)
11
2
1
3
8
6
4
8
5
10
6
9
3
1
2
8
10
4
6
5
11
7
d = X-Y
d2
2
-1
0
1
0
-4
0
2
0
-1
-1
4
1
0
1
0
16
0
4
0
1
1
Результаты
вычислений
 d2x
28,00
Коэффициент корреляции рангов xy =
0,87
Значение t-критерия с nt = n - 2 степеней свободы =
5,36
Коэффициент корреляции рангов может применяться как для количественных, так и для
качественных (описательных или атрибутивных) данных, которые допускают ранжирование.
Коэффициент корреляции рангов Спирмена вычисляется по формуле:
ρ = 1 – (6 ∑d2) / (n (n2 – 1)
где: d - разность между ранговыми номерами,
n - число членов в каждом из коррелируемых рядов.
При числе наблюдений n > 9 для оценки силы и достоверности коэффициента корреляции
рангов можно выполнить дополнительное преобразование коэффициента корреляции рангов
Спирмена к t-критерию Стьюдента:
t = ρ √ (n – 2) / (1 - ρ 2)
после чего полученное значение оценивается по соответствующей таблице t-критерия Стьюдента
для числа степеней свободы nt = n – 2.
Расчет коэффициента ассоциации
Альтернативный результат
Альтернативное условие
Да
Да
Нет
93
113,0
Коэффициент
ассоциации
0,85
Нет
72
1072,0
Коэффициент ассоциации применяется в случае альтернативной вариации данных
(заболел – не заболел, было обострение – не было или, в общем случае, да – нет)
и вычисляется по методу четырех полей по формуле:
D где: A, B, C, D – значения четырех полей для двух пар сравниваемых данных.
Оценка достоверности коэффициента ассоциации не проводится.
Информационные технологии - http://www.intexpro.ru/