Вопросы для подготовки к экзамену по дисциплине «Математика»
реклама

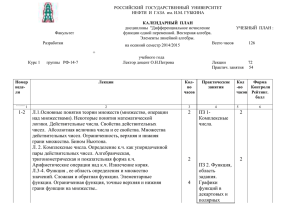
Вопросы для подготовки к экзамену по дисциплине «Математика» для 1- го курса, 1- го семестра: (гр. 510-513) Тема 1. Предел и непрерывность функции 1. Непрерывность функции в точке и на множестве, точки разрыва и их классификация. 2. Доказать непрерывность основных элементарных функций. Свойства непрерывных функций 3. Предел функции одной переменной, основные теоремы о пределах. 4. Числовая последовательность и ее предел. 5. Первый и второй замечательные пределы. Тема 2. Дифференциальное исчисление функции одной переменной 6. Понятие производной функции, ее геометрический смысл, физический и экономический смыслы . 7. Связь между непрерывностью и дифференцируемостью функции. 8. Производная алгебраической суммы, произведения, частного двух функций. 9. Производная степенной, показательной и логарифмической функций. 10. Производные тригонометрических функций. 11. Производные обратных тригонометрических функций. 12. Производная сложной, обратной, неявной функций и функции, заданной параметрически. 13. Понятие дифференциала функции и его геометрический смысл, применение дифференциала в приближенных вычислениях. 14. Производные и дифференциалы высших порядков. Правило Лопиталя. Привести примеры. 15. Теоремы Ролля, Лагранжа и Коши. 16. Необходимый и достаточный признаки возрастания (убывания) функции на интервале. 17. Понятие об экстремумах функции, необходимое условие экстремума (теорема Ферма). 18. Достаточные условия существования экстремума. 19. Необходимые и достаточные условия выпуклости (вогнутости), точки перегиба. 20. Асимптоты графика функции. 21. Схема исследования функции и построение графика. Тема 3. Дифференциальное исчисление функций нескольких переменных 22. Понятие функции нескольких переменных (ФНП), геометрическое изображение функции двух переменных, частное и полное приращение ФНП. 23. Предел и непрерывность ФНП, частные производные и их геометрический смысл для функции двух переменных. 24. Градиент функции и его свойства. 25. Полный дифференциал ФНП. Производные и дифференциалы высших порядков. 26. Необходимое и достаточное условия экстремума ФНП, нахождение наибольшего и наименьшего значения ФНП. 27. Условный экстремум ФНП. Функция Лагранжа. 28. Метод наименьших квадратов. Тема 4. Интегралы 29. Понятие первообразной, неопределенный интеграл и его свойства. 30. Таблица интегралов. 31. Основные методы интегрирования. Основные классы интегрируемых функций. Дробно- рациональные. Иррациональные. Тригонометрические. 32. Определенный интеграл и его свойства. 33. Формула Ньютона-Лейбница. Интегрирование по частям, замена переменной в определенном интеграле. 34. Геометрические приложения определенного интеграла. Длина дуги кривой. Объем тела вращения, площади поверхности вращения. Вычисление объема по площадям параллельных сечений. 35. Приближенные методы вычисления определенного интеграла. 36. Понятие о несобственных интегралах. Тема5. Дифференциальные уравнения 1- го порядка 37. Дифференциальные уравнения (ДУ) с разделяющимися переменными,. 38. Линейное ДУ первого порядка. Тема 6. Векторная алгебра 39. Понятие вектора. Линейные операции над векторами. Тема 7. Матрицы и определители 40. Понятие определителя, минора и алгебраического дополнения элементов определителя. Способы вычисления определителей. 41. Свойства определителей. 42. Понятие матрицы. Виды матриц. Действия над матрицами. 43. Обратная матрица и способы ее нахождения. Тема 8. Системы линейных алгебраических уравнений 44. Решение системы линейных уравнений в матричной форме и по формулам Крамера. 45. Решение системы линейных уравнений методом Гаусса. Тема 9. Элементы аналитической геометрии 46. Уравнение линии на плоскости. Уравнение прямой. Частные случаи. Уравнение прямой в отрезках. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки. Угол между прямыми. Кривые второго порядка. Эллипс. Кривые второго порядка. Гипербола, парабола. Доцент кафедры ЭММ _____________/И.Н. Аглиуллин/ Зав. Кафедрой ЭММ ________________/И.И. Исмагилов/