Оспанов С.С., д.ф.-м. наук, профессор КазНУ им. аль-Фараби

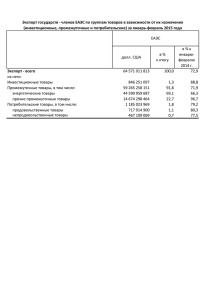
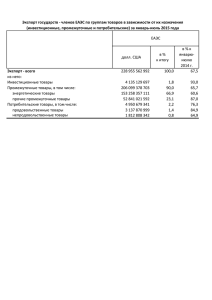
Оспанов С.С., д.ф.-м. наук,
профессор КазНУ им. аль-Фараби
Нетрадиционная транспортная модель с промежуточными пунктами
распределения сырья.
Транспортные задачи всегда входят в состав экономической системы,
которая функционирует во взаимосвязи со всеми субъектами хозяйственной
деятельности с целью обеспечения выпуска и реализации продукции.
При этом предприятия, производящие продукцию взаимодействуют с
потребителями благодаря развитой системе инфраструктуры рынка и
логистики, которые осуществляют обменные процессы.
Трансформация мировой экономической системы в сервисную
экономику стала одним из основных факторов формирования
международных целей поставок для сокращения жизненного цикла
продукции.
Внедрение новых технологий доставки грузов и развития
информационных технологий повлияли к формированию современных
подходов построения новых транспортных моделей.
Принимая во внимание ограничения:
- мощности нефтеперерабатывающих заводов и их пропускных
способностей;
- рыночные приоритеты потребителей.
Транспортные модели – это инструментарий интегрированного
управления потоками, включающие в себя базовые балансовые
соотношения между объемами предложения и спроса, а также алгоритмы
построения экономичных сетей доставки товаров и услуг.
Классические транспортные модели обычно используются для
составления экономического плана перевозок однородной продукции из
нескольких пунктов в пункты потребления с использованием следующих
исходных данных:
ai – объем производства в каждом пункте производства, i=1,2,…,m;
bj – объем спроса в каждом пункте потребления, j=1,2,…,n;
cij – стоимость транспортировки единицы продукта из пункта i в пункт
j.
– матрица стоимостей.
На основании этих данных требуется найти такую схему
транспортировки продукта, при которой общие транспортные затраты были
минимальными.
Графическая интерпретация этой постановки представима в виде
следующего двудольного графа:
a1
1
1
b1
a2
2
2
b2
am
m
n
bn
Пуст xij – количество продукции, перевозимой из пункта отправления в
пункт назначения.
Тогда транспортная задача формулируется в виде оптимизационной
матричной модели:
(1)
При ограничениях
(2)
(3)
Полагаем, что транспортная модель (1) – (3) является сбалансированной i
(4)
Стандартная транспортная модель (1) - (2) сыграла фундаментальную
роль для развития теории и методов оптимизационных моделей исследования
операций.
Многочисленные транспортные и инфраструктурные задачи
современной экономики, которые были сформулированы благодаря
достижениям в области высоких технологий, потребовали разработки
эффективных алгоритмов для решения новых транспортных и
инфраструктурных задач, связанных с определением расстояний и потоков
нематериальной природы, как информационные потоки.
Формулировки и решения практически важных задач потребовали
использование сетевых моделей, наряду с матричными моделями, для
обоснования инфраструктурных проектов.
В качестве примера можно привести задачи проектирования
газопровода и сооружения нефтепровода для разработки крупного
месторождения нефти на большой территории.
Имеются также многочисленные экономические постановки по
определению наиболее экономичной схемы транспортировки нефти,
относятся задачи доставки сырья из пунктов нефтедобычи, через
промежуточные пункты хранения и переработки продукции, к потребителям
и к пунктам распределительной системы.
К примеру, разработка месторождения Кашаган требует создания
трехуровневой системы транспортировки для доставки нефти от пунктов
производства к потребителям через промежуточные пункты.
Трехдольные модели доставки нефти от поставщика к потребителям
через промежуточные пункты приведен в двух вариантах:
- промежуточные пункты используются для буферного хранения сырья
как производителей, так и покупателей;
- промежуточные пункты между производителями и потребителями
функционируют для первоначальной переработки нефти и имеют
ограниченную емкость ее хранения.
Транспортные задачи с промежуточными пунктами отражают реальные
ситуации и описываются в матричной сетевой форме.
Решение этих моделей требует разработки специализированных
эффективных алгоритмов.
В первом варианте модели перевозка груза от пунктов производства
осуществляется через промежуточные, транзитные пункты, а также пункты
потребления.
При этих предположениях транспортную задачу с промежуточными
пунктами можно описывать с помощью двудольной оптимизационной
модели с расширенной матрицей стоимостей [1].
Графическая интерпретация этой модели представима, в виде
следующего трехдольного графа.
В транзитных пунктах, выступающих в качестве как пунктов
отправления также и пунктов назначения, объемы хранения
определяются в виде суммы объемов предложения (или потребления) и
транзита.
a1
1
1
d1
a2
2
2
d2
.
.
.
.
.
.
m
k
am
1
2
b1
b2
.
.
.
dk
n
bn
Во втором варианте перевозки от отправителей к потребителям
осуществляются через пункты первоначальной переработки с фиксированной
емкостью хранения нефти.
Графическое представление модели перевозки с пунктами
первоначальной перевозки можно изобразить в следующем виде:
а1
d1
b1
.
.
.
d2
.
.
.
b2
.
.
.
am
dk
bn
а2
Матричная модель этой транспортной постановки выражается с
помощью двух прямоугольных матриц стоимостей
и
(5)
и соответствующих им неизвестных матриц
и
(6)
Балансовые соотношения между предложением и спросом выражаются
в следующем виде.
(7)
(8)
(9)
(10)
и
для всех допустимых i, l, j в виде рекуррентных функций.
Целевые функции нетрадиционной модели с промежуточными
пунктами формулируются в виде рекуррентных функций, соответствующих
приоритетам потребителей.
Литература:
1. Хемди А. Таха. Введение в исследование операций. М.: 2007