Вопрос о вычислении Птолемеем длины тени гномона
реклама
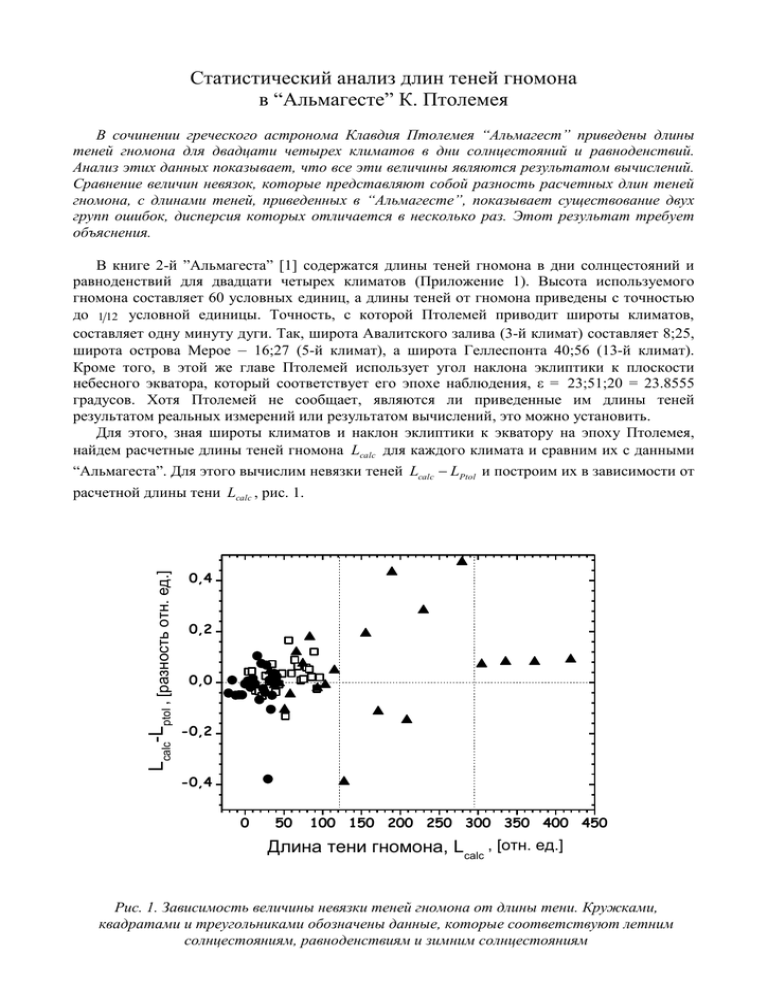
Статистический анализ длин теней гномона в “Альмагесте” К. Птолемея В сочинении греческого астронома Клавдия Птолемея “Альмагест” приведены длины теней гномона для двадцати четырех климатов в дни солнцестояний и равноденствий. Анализ этих данных показывает, что все эти величины являются результатом вычислений. Сравнение величин невязок, которые представляют собой разность расчетных длин теней гномона, с длинами теней, приведенных в “Альмагесте”, показывает существование двух групп ошибок, дисперсия которых отличается в несколько раз. Этот результат требует объяснения. Lcalc-Lptol , [разность отн. ед.] В книге 2-й ”Альмагеста” [1] содержатся длины теней гномона в дни солнцестояний и равноденствий для двадцати четырех климатов (Приложение 1). Высота используемого гномона составляет 60 условных единиц, а длины теней от гномона приведены с точностью до 1 12 условной единицы. Точность, с которой Птолемей приводит широты климатов, составляет одну минуту дуги. Так, широта Авалитского залива (3-й климат) составляет 8;25, широта острова Мерое – 16;27 (5-й климат), а широта Геллеспонта 40;56 (13-й климат). Кроме того, в этой же главе Птолемей использует угол наклона эклиптики к плоскости небесного экватора, который соответствует его эпохе наблюдения, ε = 23;51;20 = 23.8555 градусов. Хотя Птолемей не сообщает, являются ли приведенные им длины теней результатом реальных измерений или результатом вычислений, это можно установить. Для этого, зная широты климатов и наклон эклиптики к экватору на эпоху Птолемея, найдем расчетные длины теней гномона Lcalc для каждого климата и сравним их с данными “Альмагеста”. Для этого вычислим невязки теней Lcalc LPtol и построим их в зависимости от расчетной длины тени Lcalc , рис. 1. 0,4 0,2 0,0 -0,2 -0,4 0 50 100 150 200 250 300 350 400 450 Длина тени гномона, Lcalc , [отн. ед.] Рис. 1. Зависимость величины невязки теней гномона от длины тени. Кружками, квадратами и треугольниками обозначены данные, которые соответствуют летним солнцестояниям, равноденствиям и зимним солнцестояниям В таблице 1 вычислены значения средних невязок Lcalc LPtol и соответствующие им среднеквадратичные отклонения (СКО). Во втором и третьем столбцах представлены результаты расчета, полученные по всей выборке данных, в четвертом и пятом столбцах приведены результаты с отфильтрованными выбросами. Таблица 1 Среднее СКО Среднее СКО Наблюдения (все данные) (все данные) (2σ) (2σ) Летнее солнцестояние 0.091 0.049 –0.022 –0.006 Равноденствие 0.021 0.064 0.027 0.056 Зимнее солнцестояние 0.578 0.077 0.215 –0.030 Отсюда можно сделать два важных заключения. Во-первых, усредненные невязки Lcalc LPtol для летних солнцестояний и равноденствий примерно одинаковы по величине, среднеквадратичному отклонению, и соответствуют друг другу в пределах погрешности. Невязка СКО, вычисленная для зимних солнцестояний, превышает невязки СКО летних солнцестояний и равноденствий более чем в 4 раза, что требует объяснения. Во-вторых, с точки зрения анализа, важной величиной является оценка СКО для невязок равноденствий, поскольку именно она позволяет дать ответ на вопрос являются ли данные Птолемея результатами наблюдений или результатами расчетов. Оценка СКО для равноденствий позволяет получить теоретическую оценку точности, с которой наблюдатель должен уметь определять момент наступления равноденствия. Известно, что в день равноденствия склонение Солнца изменяется примерно на одну минуту дуги за один час. Поэтому погрешность определения момента равноденствия ± n часов приводит к вариации склонения ±n угловых минут. Из-за вариации склонения длина тени гномона d в момент измерения окажется чуть меньше или чуть больше длины его тени d rav в момент равноденствия. Следовательно, мы можем исследовать зависимость поведения невязок d i d i d irav от погрешности определения момента равноденствия. Считая, что ошибка определения момента наступления равноденствия подчиняется распределению Гаусса с параметрами N (0; n) , смоделируем эту ошибку и вычислим, какие при этом получатся невязки теней гномона для всех 24 климатов. Повторим эту процедуру по методу Монте-Карло 30 раз и получим 720 значений невязок, для которых вычислим среднее значение и теоретическое СКО. Проведя такую процедуру для разных значений n, построим зависимость теоретического СКО от величины ошибки определения момента равноденствия. Результаты расчетов представлены на рис. 2. В случае реальных измерений величина ошибки будет больше, по сравнению с теоретически вычисленными значениями СКО, поскольку расчет не учитывает погрешность измерения длины тени. Полученная зависимость позволяет провести обратную оценку, когда из вычисленного значения СКО можно найти погрешность определения момента равноденствия. Если воспользоваться значением СКО из таблицы 1 для равноденствий, то получим оценку погрешности времени ~ 1 часа. Иначе говоря, для того чтобы получить значение СКО ~0.05 необходимо уметь определять момент наступления равноденствия с точностью не хуже 1 часа. Кроме того, потребуется провести селекцию наблюдений, когда из всего множества должны быть отобраны только те наблюдения, в которых момент равноденствия совпадает с моментом прохождения Солнца через местный меридиан. Такая задача вполне разрешима. В работе [2] показано, что наблюдения равноденствий, выполненные греческими астрономами Метоном, Эвктемоном и Гиппархом, имеют ошибку около 7.5 часов, чему соответствует теоретическое значение СКО ~0.25. Очевидно, что при такой погрешности невозможно даже близко получить значения СКО, которые приведены в таблице 1. Следовательно, длины теней гномона являются результатом вычислений, а не измерений. 0,40 Теоретическое СКО 0,35 0,30 0,25 0,20 0,15 0,10 0,05 0,00 0 1 2 3 4 5 6 7 8 9 10 Ошибка определения момента равноденствия, [часы] Рис. 2. Теоретическая зависимость СКО невязки длины тени гномона от величины ошибки определения времени равноденствия В дополнении к сказанному заметим, что данные Птолемея по наблюдению равноденствий имеют значительно большие значения ошибок по сравнению с его предшественниками. Это дает основание считать, что Птолемей не наблюдал сам моменты равноденствий, а вычислял их. Причина расхождения состоит в неправильно принятой величине скорости прецессии 1 градус в 100 лет, поэтому мы не будем далее рассматривать наблюдения Птолемея, для которых теоретические значения СКО должны быть от 0.7 и выше. Таким образом, с помощью статистического анализа было показано, что длины теней гномона являются вычисленными величинами. Этому выводу можно найти косвенное подтверждение, если обратить внимание на то, что часть климатов и соответствующих им широт связана с протяженными объектами, например, “Страны Нижнего Египта”(№ 9), ”Середина Финикии”(№ 10), “Середина Понта” (№ 15), “Юг Британии”(№ 19)”, ”середина Британии” (№ 23). К точно локализуемым объектам относится лишь часть климатов, например, Напату (№ 6), Сиена (№ 7), Геллеспонт (№ 13). Широты самых северных климатов № 21÷№ 25, которые так же являются протяженными объектами, переданы целыми числами. По всей видимости, этим климатам широта была априорно приписана из каких-то соображений, после чего Птолемей для них вычислил продолжительность светового дня и длины теней гномона. Другим не менее важным вопросом к данным Птолемея является проблема невязок для зимних солнцестояний, у которых СКО оказывается в 4 раза больше величины СКО для летних солнцестояний и равноденствий. Основная причина отличия заключается в аномально высоких значениях невязок, которые соответствуют климатам № 12÷№ 20, рис. 1. Значение невязки, усредненное по первым двенадцати климатам, составляет L 0.024 при величине среднеквадратичного отклонения 0.080 . Хотя значение СКО примерно в 1.5 раза превышает величины СКО из таблицы 1, оно было получено на выборке вдвое меньшего объема. Если из данных по летним солнцестояниям и равноденствиям делать случайные выборки из двенадцати элементов, то получим аналогичные величины СКО. Это говорит о том, что длины теней гномона, соответствующие летним солнцестояниям, равноденствиям и первым двенадцати климатам зимних солнцестояний имеют одинаковую Lcalc-Lptol , [разность отн. ед.] статистическую точность. Длина тени гномона во время зимних солнцестояний для климатов ~ № 12÷№ 18 и № 20 имеет среднее значение L 0.162 и ~ 0.344 , что значимо отличается от всех предыдущих результатов, рис. 3. Массалия 0,6 Устье Истоки Танаиса Борисфена Юг Британии Середина Понта 0,4 0,2 0,0 Истоки Истра Озеро Меотидское -0,2 Устье Рейна [выброс] Геллеспонт -0,4 0 50 100 150 200 250 300 Длина тени гномона, L calc , [отн. ед.] Рис. 3. Зависимость величины невязки теней гномона от длины тени для климатов с наибольшими невязками. Кружками, квадратами и треугольниками обозначены данные, которые соответствуют летним солнцестояниям, равноденствиям и зимним солнцестояниям Из рис. 3 следует, что для этих же климатов, невязки соответствующие летним солнцестояниям и равноденствиям имеют значение СКО ~0.08. Это означает, что проблема высоких значений СКО для зимних солнцестояний не может являться следствием в ошибке широты. Кроме того, проверка показала отсутствие ошибок в таблице хорд (или синусов двойного угла) у Птолемея, поэтому высокие значения СКО соответствующие зимним солнцестояниям не могут быть связаны с систематической ошибкой в вычислениях. Наиболее вероятным объяснением наблюдающейся картины является предположение о том, что длины теней гномонов, приведенные в “Альмагесте”, принадлежат как минимум двум разным исследователям. Первоначально длины теней гномонов были получены в результате реальных измерений или не очень точных теоретических расчетов. В последствии, они были заменены более точным расчетом, но не полностью. Такое объяснение вполне соответствует представлениям о компилятивном характере знаний, собранных в “Альмагесте” Птолемея. Литература 1) К. Птолемей. Альмагест, М.: Физматлит, 1998. 2) Р. Ньютон. Преступление Клавдия Птолемея. М.:, “Наука”, 1985. Место 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. Остров Тапробану Залив Авалитский Залив Адулийский Остров Мерое Напату Сиена Гермиева Птолемиада Страны Ниж. Египта Середина Финикии Родос Смирна Геллеспонт Массалия Середина Понта Истоки Истра Истоки Борисфена Озеро Меотидское Юг Британии Устье Рейна Устье Танаиса Бригантий Середина Британии Катукартоний Юг Малой Британии Широта 4.2500 8.4167 12.500 16.450 20.233 23.850 27.200 30.367 33.333 36.000 38.583 40.933 43.067 45.017 46.850 48.533 50.067 51.500 52.833 54.017 55.000 56.000 57.000 58.000 Приложение 1 Длина тени в Длина тени Длина тени летнее СС в равноденствие в зимнее СС 4.417 32.000 –23.333 8.833 37.900 –16.580 13.333 44.167 –12.000 17.750 51.000 –7.750 22.167 58.167 –3.750 0.000 26.500 65.833 3.500 30.833 74.167 6.867 35.083 83.083 10.000 39.500 93.083 12.917 43.600 103.333 15.667 47.833 114.917 18.500 52.167 127.833 20.833 55.917 140.250 23.250 60.000 155.083 25.500 63.917 171.500 27.500 67.833 188.583 29.917 71.667 208.333 31.417 75.417 229.333 33.333 79.083 256.167 34.917 82.583 278.750 36.250 85.667 304.500 37.667 88.833 335.250 39.167 92.417 372.667 40.667 96.000 419.167




