Исследование магнитного поля соленоида

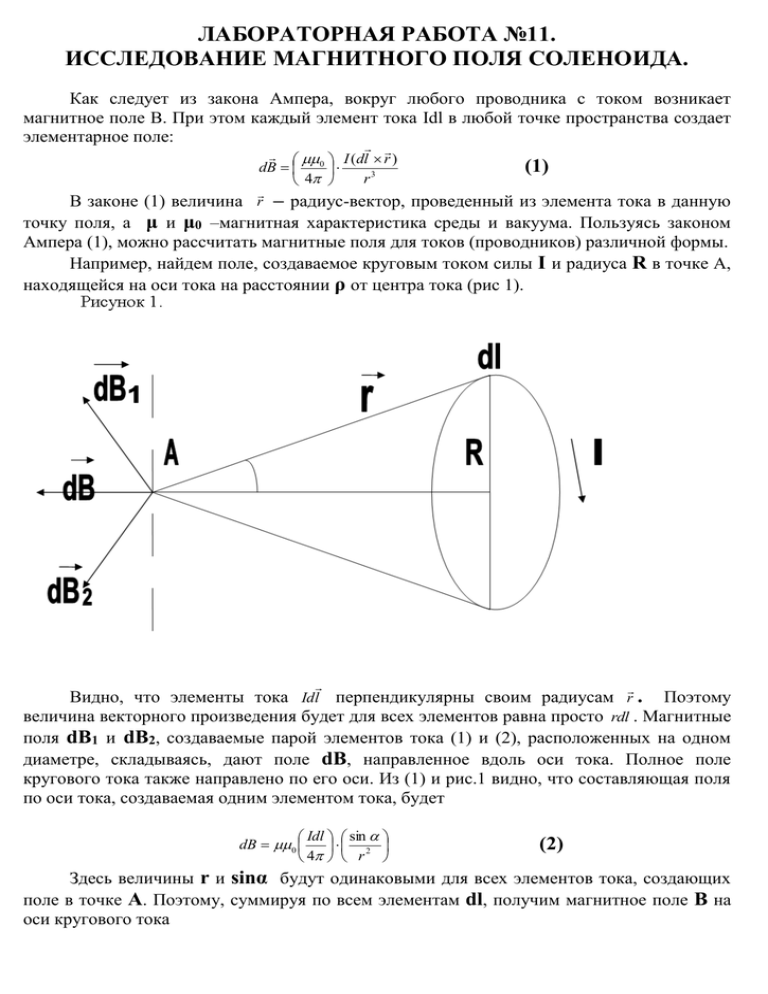
ЛАБОРАТОРНАЯ РАБОТА №11.
ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА.
Как следует из закона Ампера, вокруг любого проводника с током возникает
магнитное поле В. При этом каждый элемент тока Idl в любой точке пространства создает
элементарное поле:

  0  I (dl  r )
(1)
dB  

r3
 4 

В законе (1) величина r – радиус-вектор, проведенный из элемента тока в данную
точку поля, а μ и μ0 –магнитная характеристика среды и вакуума. Пользуясь законом
Ампера (1), можно рассчитать магнитные поля для токов (проводников) различной формы.
Например, найдем поле, создаваемое круговым током силы I и радиуса R в точке А,
находящейся на оси тока на расстоянии ρ от центра тока (рис 1).


Видно, что элементы тока Idl перпендикулярны своим радиусам r . Поэтому
величина векторного произведения будет для всех элементов равна просто rdl . Магнитные
поля dВ1 и dВ2, создаваемые парой элементов тока (1) и (2), расположенных на одном
диаметре, складываясь, дают поле dВ, направленное вдоль оси тока. Полное поле
кругового тока также направлено по его оси. Из (1) и рис.1 видно, что составляющая поля
по оси тока, создаваемая одним элементом тока, будет
 Idl   sin  
dB  0 
 2 
 4   r 
(2)
Здесь величины r и sinα будут одинаковыми для всех элементов тока, создающих
поле в точке А. Поэтому, суммируя по всем элементам dl, получим магнитное поле B на
оси кругового тока
 IR   sin  
B  0     2 
 2   r 
(3)
Другой практически важной задачей
цилиндрического соленоида на его оси (рис.2).
является
расчет
магнитного
поля
Пусть соленоид радиуса R и длины Z имеет N витков, т.е. на единицу длины
приходится n витков:
N
n
Z
(4)
Поле соленоида легко подсчитать, если воспользоваться формулой (3) и
принципом суперпозиции полей, создаваемых N витками. Для каждого витка будет свое
значение α и свое r в (3). Выделим элемент длины соленоида dz, содержащий ndz витков
с током. Поле, создаваемое этими витками, по (3) будет
 IR   sin  
dB  0     2 ndz
 2   r 
(5)
Из рисунка 2 можно видеть, что
dr  (dz ) cos 
(6)
sin   R
(7)
Так как
то, дифференцируя, будем иметь
r
 r dr
cos d   R
2
(8)
Из (5), (6) и (8), интегрируя по всем значениям угла в пределах [α1, α2], получим
B(
0
2
) In (cos  2  cos 1 )
(9)
Это и будет формула для магнитного поля цилиндрического соленоида на его оси.
Видно, что для точек наблюдения, лежащих внутри соленоида, α1<0, cosα1<0. Для очень
длинного стержня соленоида cos 1  1, cos   1 и поле внутри длинного соленоида
B  0 In
(10)
На краях длинного соленоида, где либо α1, либо α2 равны 900, поле будет
Bкр 
0 In
2
(11)
т.е. на краях длинного соленоида поле вдвое слабее, нежили в середине него.
Ту же самую формулу (10) для магнитного поля внутри соленоида можно было
вывести при помощи теоремы
о циркуляции вектора магнитной индукции. Которая гласит

что циркуляция вектора B по произвольному замкнутому контуру равна произведению
магнитной постоянной 0 на алгебраическую сумму токов, охватываемых этим контуром:
n
 
B
d
l

B
dl


0  I к (11)

 l
L
L
к 1
где n— число проводников с токами, охватываемых контуром L произвольной
формы. Каждый ток учитывается столько раз сколько он охватывается контуром.
Определим на (рис. 2) контур ABCD по которому будем проводить интегрирование (рис.
3). Стрелками обозначено направление обхода
контура при интегрировании. Также со

стрелками совпадает направление вектора B внутри и вне соленоида. Для удобства
расчетов предположим, что наш соленоид бесконечно длинный этим мы обеспечим то, что
полем вне соленоида можно будет пренебречь, т.е. поле бесконечно длинного соленоида
сосредоточено внутри него. Нам теперь необходимо найти следующий интеграл:
 B dl
l
ABCDA
Его можно разбить на следующую
сумму интегралов:
 B dl   B dl   B dl   B dl   B dl
l
ABCDA
l
AB
l
BC
l
CD
l
DA
Интегралы по отрезкам AB и CD
равны нулю т.к. на этих участках контур
перпендикулярен вектору B и его проекция
на контур Bl  0 , на участке BC поля вообще нет следовательно здесь интеграл также будет равен нулю.
Ну а на участке DA интеграл равен Bz , где z - длина охватываемого нашим контуром участка соленоида
(длина участка DA). Т.е.  Bl dl  Bz Дальше, т.к. наш контур охватывает количество витков равное N то
ABCDA
правая часть уравнения (11) примет следующий вид:  0 NI и в результате получим:
Bz  0 NI
или:
 NI
B 0
z
N
 n , и теперь если добавим среду с магнитной проницаемостью  то получим:
Где
z
B  0 In
Что является точной копией формулы (10)
(12)
(13)
При многослойной обмотке соленоида поле в точках наблюдения является
результатом наложение полей отдельных слоев, каждое из которых рассчитывается по
формуле 99). Поэтому, качественно, поле соленоида (многослойного) имеет такой же
характер, как и поле однослойного.
В данной работе магнитное поле соленоида изучается с помощью датчика Холла.
Если вдоль однородной прямоугольной пластинки металла шириной а и толщиной b
идет ток силы I в направлении оси Х, а перпендикулярно пластинке вдоль стороны b по

оси Z направим магнитное поле B , то на движущиеся заряды будет действовать сила

 
Лоренца: Fл  e(v  B)
Электроны под действием этой силы сместятся к нижней грани пластинки (рис.4), и
между верхней и нижней гранями возникнет разность потенциалов U x (Эффект Холла).
Поэтому вдоль оси Y возникнет электрическое поле E y 
U
, которое будет нарастать до тех
a
пор, пока электрическая сила eE y не уравновесит силу Лоренца evxB, т.е.
E y  vx B
Выразив поле E y через потенциал Холла U x , заменив vx  v из j  nev и, принимая во
внимание, что ток I  jba , получим
 1  IB
Ux   
 ne  b
Величину
1
принято называть постоянной Холла. Пусть
ne
1
R
ne
Тогда потенциал Холла запишется в виде
Ux  R
IB
b
Измерив потенциал Холла U x , силу тока I, толщину пластинки b и зная постоянную Холла
R, можно определить магнитное поле B.
В данной работе используется датчик Холла с b =0,4 мм; I =90мА; R =2,04 10-4 В м/А Тл
ВЫПОЛНЕНИЕ РАБОТЫ
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:
1. Соленоид: число витков N=2700
число слоев намотки =20
длина l=168 мм
диаметр первого слоя 40мм
толщина каждого слоя 1,2 мм
2. Датчик Холла в эбонитовой трубе с сантиметровыми делениями.
3. Милливольтметр.
4. Источник питания.
Примечание: соленоид и датчик Холла объединяются в блоке ФПЭ-04.
1. Собрать цепь по схеме:
2.Установить ручки регулировки тока и напряжения в крайнее левое положение и
включить источник тока.
-Включить вольтметр, дать приборам прогреться 1-2 мин.
-Установить ток в соленоиде 1 А.
-Вынуть датчик Холла из соленоида и отметить показания вольтметра U01.
-Вдвигая датчик Холла в соленоид, заполнить таблицу, учитывая, что U х= U- U01 (U –
разность потенциалов, которую показывает вольтметр).
Iсоленоида
l,мм
Uх
B=Ub/RI
-Установить ток в соленоиде 2 А, отметить U02 провести аналогичные измерения.
-Построить график для поля соленоида, т.е. кривую
Bэксп  f (I )
-Сравнить экспериментальные значения с теоретическими.