Моделирование лабораторной работы : определение удельного

1
Моделирование лабораторной работы : определение удельного
заряд электрона методом сбросового тока в вычислительной
среде Матлаб.
Целью настоящей работы была попытка моделирования движения электрона с
учетом теплового разброса вылетевших из катода электронов, а также учет
сложной зависимости скорости электрона от расстояния до катода и вытекающей
отсюда поправки к вышеуказанной формуле.
С этой целью в программной среде МАТЛАВ были написаны программы :а) моделирующие движение электронов, начальные скорости которых по величине
и по направлению распределены по нормальному закону и б)- имитирующие
эксперимент- послав значительное количество электронов ( до 1000 ед. для
каждого значения магнитной индукции ) и построить по его результатам
сбросовую кривую.
Результаты моделирования представлены на следующих рисунках с
комментариями.
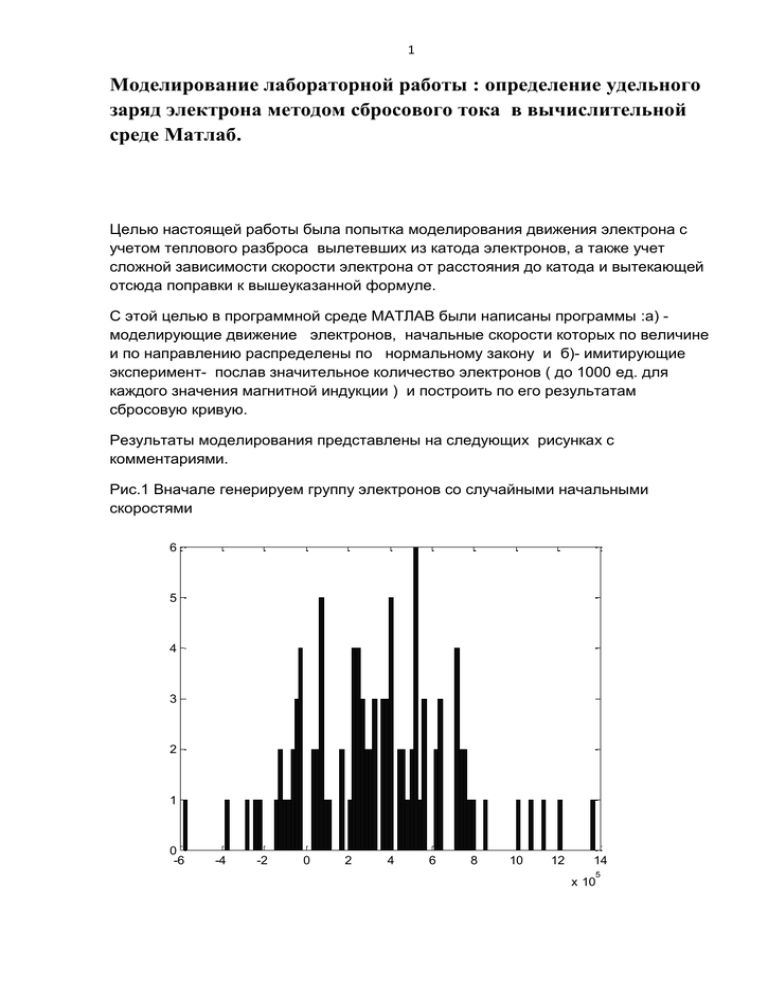
Рис.1 Вначале генерируем группу электронов со случайными начальными
скоростями
6
5
4
3
2
1
0
-6
-4
-2
0
2
4
6
8
10
12
14
5
x 10
2
Гистограмма значений скоростей 100 электронов, эмитируемых катодом лампы
при температуре Т=2000 К.
-3
trajectory of electrone
x 10
8
6
y-axis,m
4
2
0
-2
-4
-6
-6
-4
-2
0
2
4
x-axis,m
6
8
10
12
14
-3
x 10
Рис.2 При напряжении анод-катод около 10 вольт вычисляем траекторию
электрона. Катоду соответствует круг зеленого цвета(r=7мм) , аноду –
красного(R=15 мм). Магнитное поле – выключено
trajectory of electrone
y-axis,m
0.01
0
-0.01
-0.02
-0.025
-0.02
-0.015
-0.01
-0.005
0
x-axis,m
0.005
Рис . 3 Магнитное поле включено. Ток =1А
0.01
0.015
3
trajectory of electrone
0.015
0.01
y-axis,m
0.005
0
-0.005
-0.01
-0.015
-0.015
-0.01
-0.005
0
x-axis,m
0.005
0.01
0.015
Рис .4 Магнитное поле включено. Сила тока 1.3 Ампера.
6
4.5
v -dependence of r
x 10
4
3.5
v-axis,m/sec
3
2.5
2
1.5
1
0.5
0
0
0.05
0.1
0.15
0.2
0.25
r-axis,m
Рис.4 Зависимость скорости электрона от расстояния до оси лампы (Сила тока
=0)
4
6
3
v -dependence of r
x 10
2.5
v-axis,m/sec
2
1.5
1
0.5
0
0.006
0.008
0.01
0.012
0.014 0.016
r-axis,m
0.018
0.02
0.022
0.024
Рис. 5. Та же зависимость : 20 кривых – разные начальные скорости электронов.
Из приведенных рисунков следует, что скорости электронов сильно меняются
5
100
90
80
70
60
50
40
30
20
10
0
0.8
1
1.2
1.4
1.6
1.8
2
Рис.6 Сбросовая кривая для случая 100 электронов, рандомизированных по
скоростям и углам вылета. По горизонтальной оси – сила тока в амперах, по
горизонтальной – в относительных единицах – сила тока через лампу.
Листинг программы Mgntrnrndn.m
clear all
U=input('введите U- анодное напряжение В (12V)
')
R1=7;
R2=15;
% R1=input('введите R1- радиус катода в мм. ')
% R2=input('введите R2- радиус анода в мм. ')
m=9*10^-31;
e=-1.6*10^-19;
% среднеквадратичная скорость электронов для т-ры 2000 С
v0=(1+randn(1,100))*3*10^5;
hist(v0,100)
pause
% v0(2)
% v0=input('введите начальную скорость электрона v0 (10^5)
% alf=input('введите угол вылета электрона (0-90)
')
% alf=45
% alfa=alf*2*pi/360
')
6
alfa=2*pi*rand(1,100);
vx0=v0.*cos(alfa);
vy0=v0.*sin(alfa);
% dt=input('введите шаг по времени dt(10^-11 c)
')
dt=3*10^-11;
I0=input('начальный ток в соленоиде I0(A) ')
Imax=input('максимальный ток в соленоиде I0(A) ')
% n=input('введите n число витков на единицу длины соленоида
')
n=1200;
A=U/log(R2/R1);
C=e/m;
% N=input('введите число шагов по времени ')
N=2000;
kmax=input('введите число значений тока соленоида ')
for k=1:kmax;
I(k)=I0+k*(Imax-I0)/kmax ;
Bz(k)=(4*pi*10^-7)*n*I(k);
for j=1:1:100
vx0(j)=v0(j)*cos(alfa(j));
vy0(j)=v0(j)*sin(alfa(j));
for i=1:N;
vx(1,j)=vx0(j);
vy(1,j)=vy0(j);
x(1,k)=R1*10^-3;
y(1,k)=0;
ax(1,k)=0;
ay(1,k)=0;
% ускорение обусловено магнитной и электричекой составляющей
% силы Лоренца: a=evb+eE где Е=
%%
ax(i+1,j)=-C*(vy(i,j)*Bz(k)+A*x(i,k)/(x(i,k).^2+y(i,k).^2));
ay(i+1,j)=-C*(-vx(i,j)*Bz(k)+A*y(i,k)/(x(i,k).^2+y(i,k).^2));
vx(i+1,j)=vx(i,j)+ax(i+1,j)*dt;
vy(i+1,j)=vy(i,j)+ay(i+1,j)*dt;
v(i,j)=sqrt(vx(i,j).^2+vy(i,j).^2);
x(i+1,k)=x(i,k)+vx(i+1,j)*dt+0.5*ax(i+1,j)*dt.^2;
y(i+1,k)=y(i,k)+vy(i+1,j)*dt+0.5*ay(i+1,j)*dt.^2;
r(i,k)=sqrt(x(i,k).^2+y(i,k).^2);
if r(i,k)>R2*10^-3;
nmb(j,k)=1;
S=sum(nmb);
end
t(i,k)=i*dt;
end
end
end
I
S
n=size(I)
m=size(S)
n(2)
m(2)
7
M=m(2)+1:n(2)
k(2)=n(2)-m(2)
s(1:k(2))=0
S1=cat(2,S,s)
pause
plot(I,S1)
grid on
На основании приведенных модельных опытов была предложена поправка в
формулу для e/m в виде коэффициента в числителе формулы 0.43.