Литература Файл
реклама

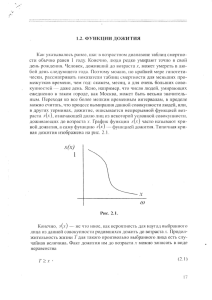
Введение в описательную статистику и некоторые статистические функции MS Excel «Необобщенные данные — не более чем сплетня». Постулат Пирсинга. Результатом любых измерений одного или нескольких признаков будет являться множество данных, которые для последующей интерпретации, должны быть обработаны методами математической статистики. Реально наблюдаемая совокупность объектов, статистически представляемая рядом наблюдений Х1,Х2,Х3…Хn случайной величины Х, называется выборкой, а гипотетическая существующая (домысливаемая) – генеральной совокупность. В предметной биологии генеральную совокупность можно интерпретировать как мыслимое множество вариант, сформированных при одинаковых (внешних и внутренних) условиях. Например, чистая линия инфузорий (дафний), выращенных при температуре помещения 200С. Возможно, что кроме этих конкретных инфузорий, в природе больше не существует таких же, выращенных при этих условиях. Все равно, в определении генеральной совокупности важно не реальное ее существование, а мыслимое однообразие условий, порождающих эти выборки. Отличие генеральных значений от выборочных оценок состоит в том, что в первом случае они рассчитаны по всем вариантам, а во втором – по ограниченному их числу. Поэтому, чем меньше объем выборок, тем менее точными будут выборочные оценки каких-либо параметров, и, напротив, чем больше выборка, тем ближе выборочные значения к генеральным («закон больших чисел»). Выборка образуют вариационный ряд, если все выборочные значения случайной величины Х упорядочены по возрастанию, значения признака, называют вариантами. Одной из важнейших обобщающих характеристик вариационного ряда является средняя величина признака (обозначается буквой М). Существует не- сколько видов средних, но в биологии часто распространена средняя арифметическая величина (М или Х). Общая формула для определения величины средней арифметической – это отношение суммы значений всех вариант (Хi) выборки к их числу (объему выборки, n) В программе Excel значение средней арифметической вычисляет функция =СРЗНАЧ(диапазон). Диапазоном может быть один или несколько столбцов значений. Стандартное отклонение (S, SD, σ) – мера разнообразия входящих в группу объектов и показывает, на сколько, в среднем отклоняются варианты от средней арифметически изучаемой совокупности. Рабочая формула, используемая для расчета стандартного отклонения, учитывает сумму квадратов значений признака для всех вариант, сумму значений признака и объем выборки. В программе Excel стандартное отклонение вычисляется с помощью функции =СТАНДОТКЛОН(диапазон). Стандартное отклонение позволяет сравнивать характер варьирования лишь одних и тех же признаков. Чтобы сопоставить изменчивость разнородных признаков, выраженных в разных единицах измерения или нивелировать влияние масштаба измерений, используют коэффициент вариации (CV) – отношение стандартного отклонения к собственной средней М (или Х): CV= (SD/Х)×100% Методом отнесения стандартных отклонений к соответствующим средним, они переводятся в соизмеримые величины и освобождаются от влияния величины самого признака. Практика показывает, что для многих показателей наблюдается увеличение стандартного отклонения с ростом их величины (средней арифметической), однако коэффициент вариации, остается на прежнем уровне. За увеличение CV ответственны растущие отличия распределения признака от нормального закона. Распределение – это соотношение между значениями случайной величины и частотой их встречаемости. Если значения признака откладывать по оси абсцисс, а частоты встречаемости – по оси ординат, то можно построить гистограмму. Гистограмма, приведенная на рисунке 1, имеет вид холмика и называется нормальным распределением. Большее количество значений признака (содержание гемоглобина) будет находиться в районе среднего значения. Рисунок 1. Пример нормального распределения результатов (среднее 95,0, стандартное отклонение 20,0 г/л). Серыми столбцами показано распределение уровня гемоглобина. Другие варианты распределения представлены в боксе Вероятностные распределения Виды переменных Одномерные Многомерны Бернулли | Биномиальное | Геометрическое | Гипергеометрическое | Дискретные: Логарифмическое | Отрицательное биномиальное | Пуассона | Дискрет- Мультиномиально ное равномерное Бета | Вейбулла | Гамма | Гиперэкспоненциальное | Распределение Гом- Абсолютно непрерывные: пертца | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | Логистическое | Накагами |Парето | Полукруговое | Непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | Хи-квадрат | Многомерное мальное | Копула Экспоненциальное | Variance-gamma Однако несмотря на большое количество вариантов, чаще всего в медикобиологических экспериментах распределение показателей может быть условно отнесено к нормальному для непрерывных переменных и к биномиальному для дискретных переменных. При этом важно в каждом отдельном случае правильно оценивать степень апроксимации. Еще одной характеристикой вариационного ряда является доверительный интервал – это интервал, в котором с заданной вероятностью ожидается присутствие генерального параметра, границы такого интервала, называются доверительными. Для того чтобы доверительный интервал имел числовое отображение, условились, что он будет равен такому диапазону, в который попадает 95% значений, т.е., вероятность того что величина находится вне доверительного интервала меньше 5%. Это относится не к выборке, которую мы можем сплошь и поперек измерить, а к популяции, многие из членов которой нам не доступны. Возвращаясь к рисунку 1, можно констатировать, что все значения признака расположены в форме симметричной колоколообразной кривой. При этом, в пределах одного стандартного отклонения от среднего (1σ) находится 68% всех значений признака (на рисунке это интервал 75-115 г/л), в пределах двух стандартных отклонений (2σ) от среднего находится 95% всех значений признака (интервал 55-135 г/л – доверительный интервал для этой выборки), и в пределах трех стандартных отклонений находится 99,5% всех значений признака. Интервал (М-3σ; М+3σ) является почти достоверным, так как подавляющее большинство отдельных результатов многократного измерения случайной величины окажется сосредоточенным именно в нем. При обработке результатов эксперимента часто используется «правило 3σ», или правило «трех стандартов», которое основано на указанном свойстве нормального распределения. С учетом проведенного выше анализа, можно установить наличие промаха в результате отдельного измерения, а значит, отбросить его, если результат измерения более чем на 3σ отличается от измеренного среднего значения случайной величины. В то же время стоит более тщательно повторить измерения в этой области параметров – возможно, данный результат измерения не является промахом, а свидетельствует о наличии необычного поведения изучаемой системы, которое не укладывается в рамки существующей модели В практике медико-биологических исследований нередки случаи, когда числовые значения признаков, дают распределения, отличающиеся от нормального (рис.2). При асимметричном распределении (Рис.2А) наблюдается появление «хвоста», а для эксцессивного характерно чрезмерное накопление или снижение частот в центральных классах вариационного ряда (рис. 2Б). При отклонениях распределения переменной от нормального в интервале M±2 уже может не содержаться 95% значений. А. Б. Рисунок 2. Ненормальное распределение значений: А) асимметрия Б) эксцесс Для таких распределений понятия среднее и стандартное отклонение утрачивают смысл, поскольку они дают неправильное описание распределения переменной. Распределения, отличные от нормального, принято описывать при помощи медианы, перцентилей и интерквартильного размаха. Медиана – это значение признака, которое делит весь ряд значений по возрастанию пополам, то есть половина значений признака меньше медианы, и половина – больше ее. При больших массивах, данных в ручную определение медианы является трудоемкой операцией. В программе Excel медиана вычисляется с помощью функции =МЕДИАНА(диапазон). Перцентиль – это накопленный (суммированный) процент встречаемости конкретного результата, который складывается из процента встречаемости выбранного результата и всех предшествующих ему результатов. Перцентильные значения (ранги) рассчитываются для того, чтобы разграничить континиум полученных результатов на три зоны значений, т.е. научно обоснованно прове- сти границы между зонами «высоких», «средних» и «низких» результатов. Это делается для того, чтобы впоследствии каждый индивидуальный результат можно было отнести к одной из этих трех зон и построить заключение об уровне полученного результата. Величины перцентилей, которые разграничивают три зоны, называются «критическими перцентилями». Они соответствуют таким величинам, как 25-й и 75й перцентили. Это означает, что все экспериментальные результаты, которые укладываются по своей частоте встречаемости в диапазон от 1-го до 25-го перцентиля включительно, относятся к зоне «низких» значений. В зону «средних» значений попадают результаты, которые оказываются в диапазоне от 26-го по 75-й перцентиль включительно. А зоне «высоких» значений соответствуют результаты, относящиеся к диапазону от 76-го до 100-го перцентиля включительно. Медиана является 50-ым перцентилем. Интерквартильный размах – это интервал между 25 и 75 перцентилями, то есть четверть всех значений признака будут меньше 25 перцентиля, а четверть – больше 75 перцентиля. Таким образом, интерквартильный размах содержит «центральные» 50% значений признака. В принципе, понятие медианы и интерквартильного размаха вполне применимо и к нормальному распределению. В этом случае медиана будет равна среднему, а в пределах интерквартильного размаха будет находиться чуть меньше значений (50% всех значений), чем в пределах одного стандартного отклонения (68% всех значений). Для проверки распределения полученных экспериментальных данных следует рассчитать среднее арифметическое и медиану значений выборки, в случае их совпадения, распределение нормальное, если они не совпадают - ненормальное. Исходя из типа распределения данных, следует выбирать дальнейшие статистические параметры. Завершением обработки данных многократного прямого измерения при заданной доверительной вероятности являются два числа: среднее значение из- меренной величины и его погрешность (полуширина доверительного интервала). Оба числа есть окончательный результат многократного измерения и должны быть совместно записаны в стандартной форме: x±Δx, которая содержит только достоверные, т.е. надежно измеренные, цифры этих чисел. Статистический вывод и проверка гипотез Кроме чисто описательной, другими задачами, которые решает прикладная статистика являются статистический вывод, планирование эксперимента и определение объема выборки, сравнение нескольких переменных, анализ выживания, выявление корреляции и регрессии. Подробности теории статистического анализа рассматриваются в специальной литературе. Разделы Статистические показатели и технологии Доверительный интервал (Частотная вероятСтатистический ность) · Достоверный интервал (Байесовский вывывод вод) · Статистическая значимость · Мета-анализ Генеральная совокупность · Планирование выборПланирование ки · Районированная выборэксперимента ка · Репликация · Группировка · Чувствительность и специфичность Статистическая мощность · Мера эффекта · Стандартная ошибОбъём выборки ка Байесовская оценка решения · Метод максимального правдопоОбщая оценка добия · Метод моментов нахождения оценок · Оценка минимального расстояния · Оценка максимального интервала Z-тест · t-критерий Стьюдента · Критерий Фишера · Критерий Пирсона (Хи-квадрат) · Критерий согласия Колмогорова · Тест Сравнение переменных Вальда · U-критерий Манна — Уитни · Критерий Уилкоксона · Критерий Краскела — Уоллиса · Критерий Кохрена · Критерий Лиллиефорса Функция выживания · Оценка Каплана — Мейера · ЛогранкАнализ выживания тест · Интенсивность отказов · Пропорциональная модель опасностей Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляКорреляция ций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания Основная линейная модель · Обобщённая линейная моЛинейные модели дель · Анализ вариаций · Ковариационный анализ Линейная · Нелинейная · Непараметрическая регресРегрессия сия · Полупараметрическая регрессия · Логистическая регрессия Многообразия статистических процедур делает выбор оптимального теста чрезвычайно сложной задачей. Никогда не следует забывать, что статистиче- ские технологии — это просто инструмент в то время как решение о применении того или иного метода и объяснение результата должно, в первую очередь, основываться на здравом смысле экспериментатора. Мы рассмотрим только некоторые задачи и приемы статистического анализа, наиболее часто применяемые в медико-биологических экспериментах. Определение оптимального количества наблюдений при определении референтных интервалов. Очевидно, что с увеличением количества наблюдений среднее квадратичное отклонение выборки будет уменьшаться, однако до тех пор, пока не достигнет значения общей вариации. При дальнейшем увеличении количества наблюдений возможны некоторые незначительные колебания вокруг ее значения. Поэтому при определении референчных интервалов для количественного теста достаточно такое количество наблюдений при котором величина среднего квадратичного отклонения становится постоянной. Надо дописать и рисунок вставить из русской работы Определение оптимального количества наблюдений для доказательства тождественности выборок. Это нередкая задача, напрмер в фармакологии она ставится при внедрении в медицинскую практику генериков. В статистике она решается через расчет мощности критерия. мощности статистического критерия определяется как вероятность отвергнуть нулевую (основную) гипотезу при заданном распределении наблюдений P. Функция мощности является функцией от распределения P наблюдаемых случайных величин. В случае, если P соответствует нулевой гипотезе, значение функции мощности называется вероятностью ошибки первого рода. Если P соответствует альтернативной гипотезе, то значение функции мощности называют просто мощностью. Для критерия, основанного на выборке фиксированного объема, мощность равна единице минус вероятность ошибки второго рода. Поэтому минимизировать вероятность ошибки второго рода означает максимизировать мощность. Отсюда - наиболее мощные критерии. дописать Доказательства различия выборок Исследование Одна группа до и после Более двух лечения Признак Две группы групп КоличественныйКритерий ДисперсионныйПарный кри(распределение Стьюдента анализ терий Стьюнормальное*) дента Качественный Критерий X2 Критерий X2 Порядковый Критерий Критерий Манна- Уит- Крускала— ни Уоллиса Выживаемость Критерий Гехана Одна группа, несколько ви- Связь признадов лечения ков ДисперсионныйЛинейная реанализ повтор- грессия, корных измерений реляция или метод Блэнда—Алтмана Критерий Критерий Кок- Коэффициент Мак- Нимара рена сопряженности Критерий Критерий Коэффициент Уилкоксона Фридмана ранговой корреляции Спирмена Анализ кривых дожития Построение таблиц дожития (life tables) – метод оценки кривой выживаемости в анализе выживаемости. Одна из основных задача анализа выживаемости – получить оценку функции выживания или функции распределения, а также ожидаемого среднего времени жизни. Наиболее часто используемые параметрические методы непригодны для оценки параметров в анализе выживаемости. Таблица дожития – таблица, описывающая распределение времени до наступления определенного анализируемого события. Таблица дожития содержит обобщенные данные о продолжительности «жизни» и времени «смерти» для определенной совокупности наблюдений. Ключевым показателем для построения таблиц дожития является количественная переменная, характеризующая продолжительность жизни для каждого наблюдения. На основании количественной переменной продолжительности времени жизни рассчитывают следующие показатели таблиц дожития: абсолютные – число доживших или умерших до определенного момента времени; относительные – доля доживших или умерших до определенного момента времени; показатели точности оценивания показателей в таблице дожития. При построении таблиц дожития анализируют некоторое критическое событие. Критическое событие – событие риска, которое приводит к исключению объекта из выборки наблюдений. Например, при анализе продолжительности жизни пациента смерть будет являться критическим событием. Общий алгоритм построения таблиц дожития следующий: разбить временной период возможного наступления критических событий на интервалы; для каждого интервала вычислить абсолютные и относительные показатели, позволяющие оценить вероятности событий, произошедших на этом отрезке времени; оценить общую вероятность анализируемого события в различные моменты времени. С помощью таблиц дожития можно получить точную оценку кривой дожития при отсутствии цензурированных данных. Чем больше цензурированных данных, тем менее точнее будет происходить оценка функции дожития. При нали- чии цензурированных данных для оценки функции дожития предпочтительнее использовать метод Каплана-Мейера для построения таблиц дожития – это метод оценки кривой дожития при наличии цензурированных данных. Оценка функции выживания методом таблиц дожития предполагает предварительную группировку данных и зависит от числа и ширины интервалов времени жизни. Оценка функции выживания по методу Каплана-Мейера происходит без разбиения исходных данных на временные интервалы.