УДК 532.526.5:519.63 ВЛИЯНИЕ ГРАНИЧНЫХ УСЛОВИЙ НА РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ОТРЫВНОГО ПУЛЬСИРУЮЩЕГО

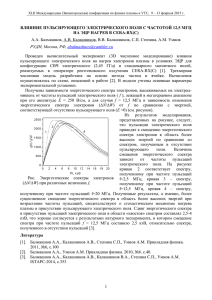
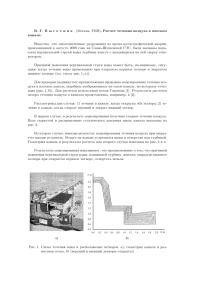
УДК 532.526.5:519.63
ВЛИЯНИЕ ГРАНИЧНЫХ УСЛОВИЙ НА РЕЗУЛЬТАТЫ
МОДЕЛИРОВАНИЯ ОТРЫВНОГО ПУЛЬСИРУЮЩЕГО
ТУРБУЛЕНТНОГО ТЕЧЕНИЯ
С.В. Болдырев, ассистент, г. Набережные Челны, Российская
Федерация, underminder@mail.ru,
А.В. Болдырев, к.т.н., г. Набережные Челны, Российская Федерация,
alexeyboldyrev@mail.ru,
И.Х. Исрафилов, д.т.н., профессор, г. Набережные Челны, Российская
Федерация, irmaris@yandex.ru,
С.И. Харчук, к.ф.-м.н., доцент, г. Казань, Российская Федерация,
kharchyk@mail.ru
Функционирование гидро- и пневмоаппаратов часто сопровождается одновременным возникновением пульсаций и отрывов потока. Причем колебания
течения генерируются как при периодическом движении узлов агрегата в его
проточной полости, так и при выходе аппарата на неустойчивые режимы работы вследствие внешнего возмущающего воздействия (автоколебания запорных
элементов клапанов и т.п. [1-2]). Наложенные пульсации вызывают изменение
характеристик и структуры течения, приводят к резонансным и другим явлениям. С одной стороны их можно создавать для управления отрывом потока [3], а
с другой – они могут приводить к быстрому износу устройств и др. Этим объясняется большой интерес исследователей к данному классу течений.
В настоящей работе исследовано влияние граничных условий и величины
временного шага на результаты численного моделирования осесимметричного
пульсирующего отрывного турбулентного течения вязкого сжимаемого газа
(воздуха) за диафрагмой, расположенной на входе в цилиндрический канал.
Математическая модель, составленная в программном пакете STARCCM+ [4], включала в себя осредненные по Рейнольдсу уравнения НавьеСтокса, неразрывности и энергии, уравнение Клапейрона, уравнения высокорейнольдсовой квадратичной k- модели турбулентности с пристеночными
функциями.
1
Рисунок 1 – Граничные условия
Рисунок 2 – Распределение коэффициента поверхностного трения вдоль стенки
канала для квазистационарного и пульсирующего с частотой 230 Гц отрывных
турбулентных течений
Для тестирования математической модели использованы экспериментальные данные [3] для течения воздуха (средний расход 0,053 м3/с), в котором
за счет вращения заслонки, периодически перекрывающей выходное отверстие
канала, создавались пульсации расхода с частотой f = 0-377 Гц.
Форма и размеры расчетной области (рис.1) максимально приближены к
параметрам экспериментальной установки [3]. Всасывание воздуха из атмосферы и попадание из канала в ресивер смоделировано с помощью полусфериче2
ских областей. На первом этапе исследований колебания генерировались с помощью гармонической функции изменения массового расхода на выходе (на
входе в канал задавалось постоянное статическое давление). Однако в этом
случае не было выявлено наблюдаемого в экспериментах [3] изменения средней
длины отрывной зоны. Поэтому на втором этапе исследований на выходной
границе задавался постоянный средний массовый расход, а пульсации создавались путем периодического изменения во времени площади выходного сечения
канала S(t) с использованием деформирующихся расчетных сеток.
Дискретизация расчетной области осуществлена с помощью сетки из 1,6
млн. ячеек квадратной формы со сгущением вблизи стенок (y+ ≥ 30) и в зоне рециркуляции. При моделировании нестационарных течений шаг по времени составил 10-6 с. Число итераций внутри каждого временного шага выбиралось из
условия снижения уровня невязок минимум до 10-4.
Значения осредненного по времени коэффициента поверхностного трения
CF определены вдоль стенки канала через каждые 10-4 с и нормированы с использованием средней по времени и по сечению скорости потока в канале. При
частоте пульсаций f = 230 Гц (рис.2), получено сокращение средней длины отрывной зоны почти в 1,4 раза по сравнению с вариантом f = 0 Гц. Однако данный эффект сильно занижен по сравнению с экспериментом. Дальнейший анализ результатов моделирования показал, что при низких частотах достигается
как качественное, так и количественное соответствие экспериментальным данным. В то же время при высокочастотных колебаниях протяженность отрывной
зоны изменяется слабее, чем в натурном эксперименте, а погрешность расчета
коэффициента Cf достаточно высока.
Расчетами подтверждено наличие экстремума для зависимости относительной длины отрывной зоны от числа Струхаля (рис.3), однако по сравнению
с экспериментальными данными [3] положение экстремума соответствует области больших значений частоты пульсаций.
Рисунок 3 – Изменение относительной длины отрывной зоны в зависимости от
числа Струхаля: слева – эксперимент, справа – расчет для Re = 33000
3
Рисунок 4 – Распределение безразмерной энергии турбулентных пульсаций
вдоль оси канала (слева) и относительная амплитуда пульсаций осевой скорости вблизи диафрагмы (справа) при различных частотах наложенных пульсаций
В ходе расчетов замечено увеличение кинетической турбулентной энергии (рис.4, слева) на пульсирующих режимах по сравнению с квазистационарным, а также некоторое смещение зоны максимальных пульсаций к диафрагме
при увеличении частоты f, тем не менее, положение данной зоны каждый раз
оказывалось несколько ниже по течению, чем в экспериментах [3].
Зависимость относительной амплитуды пульсаций осевой скорости вблизи диафрагмы от частоты пульсаций f (рис.4, справа) также свидетельствует о
снижении точности расчета пульсационных характеристик течения на высокочастотных режимах.
Для исследования влияния величины временного шага на результаты моделирования применены значения из диапазона t = 10-7…10-4 с. Выявлено, что
при данных условиях величина временного шага не оказывает существенного
влияния на протяженность отрывной зоны. Погрешность расчета коэффициента
Cf в отрывной зоне при уменьшении временного шага сначала растет, а со значения 10-7 с – начинает уменьшаться.
Таким образом, полученные результаты говорят о необходимости модификации квадратичной k- модели турбулентности для более адекватного учета
влияния наложенных пульсаций на параметры течения. При этом в расчетах
целесообразно генерировать пульсации путем периодического изменения площади выходного сечения канала.
4
СПИСОК ЛИТЕРАТУРЫ
1. Попов Д.Н. Механика гидро- и пневмоприводов: учебник для вузов.
– М.: МГТУ им. Н.Э. Баумана, 2001. – 320 с.
2. Салман М.И. Совершенствование электрогидравлических следящих
приводов с пропорциональным управлением золотниковым распределителем /
Автореф. дисс. канд. тех. наук / Москва. – МГТУ им. Н.Э. Баумана. – 2013.
3. Давлетшин И.А. Гидродинамические и тепловые процессы в пульсирующих турбулентных потоках: дис. докт. техн. наук. – Казань, 2009. – 298 с.
4. User Guide STAR-CCM+ Version 8.02.011. – CD-adapco, 2013.
5