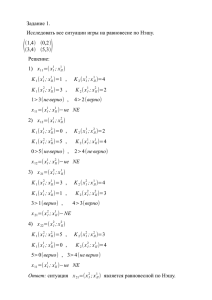Домашнее задание 62013-09
реклама

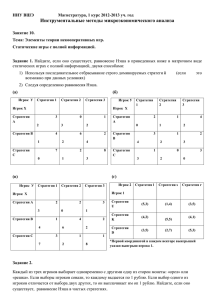
Рассмотрим следующую игру: s1 s2 t1 1;-1 6;-6 t2 3;-3 0;0 t3 0;0 9;-9 t4 4;-4 -3;3 1. Найдите все равновесия Нэша в чистых стратегиях. 2. Найдите все равновесия Нэша, в которых первый игрок играет чистую стратегию, а второй игрок смешивает стратегии. Далее считаем, что первый игрок играет смешанную стратегию αs1+(1-α)s2, где 0 < α < 1. 3. Для каждой чистой стратегии второго игрока определите его ожидаемые выигрыши при использовании этой стратегии (напомним, что первый игрок играет стратегию αs1+(1-α)s2). 4. Постройте «стакан». Для каждого значения α, 0 < α < 1, определите наилучший ответ второго игрока на стратегию первого αs1+(1-α)s2. При каких α второму игроку имеет смысл смешивать стратегии? 5. Рассмотрим случай тех α, для которых оптимальный ответ второго игрока может быть только чистой стратегией (обозначим оптимальный ответ второго через BR2(α); здесь BR – сокращение от Best Response (наилучший ответ)). Проверьте, является ли стратегия αs1+(1-α)s2 оптимальным ответом первого игрока на стратегию BR2(α) второго. Найдите все равновесия Нэша, соответствующие этому случаю. 6. Рассмотрим случай тех α, для которых второму игроку может быть выгодно смешивать стратегии. В общем случае смешанная стратегия второго игрока имеет вид β1t1+β2t2+β3t3+β4t4, где 0 ≤ β1, β2, β3, β4 ≤ 1. Используя соображение о том, что раз первый игрок смешивает стратегии s1 и s2, то эти две чистые стратегии приносят ему одинаковый ожидаемый выигрыш, определите коэффициенты β1, β2, β3, β4. Является ли стратегия αs1+(1-α)s2 оптимальным ответом первого игрока на стратегию β1t1+β2t2+β3t3+β4t4 второго? Найдите все равновесия Нэша, соответствующие этому случаю. 7. Выпишите все равновесия Нэша в смешанных стратегиях в этой игре.