Вариант 7. м = 20 м/с
реклама

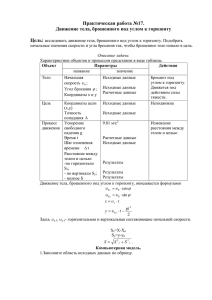
Вариант 7. В последнюю секунду свободно падающее тело прошло 20 м. С какой высоты и сколько времени падало тело, с какой скоростью достигло тело земли? Вариант 7. Камень, брошенный горизонтально на высоте H = 60 м над землей, упал на расстоянии x = 71 м от места бросания (считая по горизонтали). Найти его начальную и конечную скорости (v0 и v). Вариант 7. Камень, брошенный со скоростью v0 = 20 м/с под углом = 45° к горизонту, упал на землю на расстоянии x от места бросания. С какой высоты H надо бросить камень в горизонтальном направлении, чтобы при той же начальной скорости v0 он упал на то же место? Вариант 7. С высоты H = 20 м вниз под углом к горизонту = 60° брошен мяч с начальной скоростью v0 = 25 м/с. Определить расстояние x между абсциссой точки бросания и местом первого удара мяча о землю. Вариант 7. Шар массой m1 = 2 кг, испытал упругое столкновение с неподвижным шаром массой m2 = 8 кг. Какую относительную часть кинетической энергии потерял налетающий шар, если столкновение лобовое? Вариант 7. При постоянном давлении моль водяных паров, занимавший объем V1= 27,9 л, был нагрет от температуры t1= 129 oC до t2 = 228 oC. Начальное давление водяных паров P = 120 кПа. Определить конечный объем V2 и работу расширения газа A. Вариант 7. В закрытом сосуде объемом V = 10 л находится моль воздуха при давлении P1 = 199 кПа. Какое количество тепла Q надо сообщить воздуху, чтобы повысить давление в сосуде в 2 раза? Вариант 7. Моль газа объемом V1 = 10 л при изотермическом расширении изменяет давление от P1 = 164 кПа до P2 = 42 кПа. Определить температуру T, конечный объем V2 газа и работу расширения A. Вариант 7. Моль одноатомного газа, занимающий объем V1 = 40 л при температуре t1 = 27 oC, сжали адиабатически так, что давление его увеличилось в 2 раза. Определить конечные объем V2, температуру t2 и изменение внутренней энергии газа. Вариант 7. Наименьший объем моля газа, совершающего цикл Карно, V1 = 10 л, а наибольший V3 = 40 л. Объем газа в конце изотермического расширения V2 = 20 л, а в конце изотермического сжатия V4 = 18 л. Определить с помощью компьютерной модели к.п.д. цикла и температуры нагревателя T1 и холодильника T2. Вариант 7. Найти индукцию магнитного поля в точке, отстоящей на r1 = 1,5 м от бесконечно длинного прямого провода, по которому течет ток силой I1 = 2 А. Вариант 7. Два прямолинейных длинных параллельных проводника находятся на некотором расстоянии r1 = 0,75 м друг от друга. По проводникам текут токи, равные по величине и по направлению. Найти силу тока, текущего по каждому из проводников, если известно, что сила взаимодействия на единицу длины проводников равна F = 0,864 мкН. Вариант 7. В однородном магнитном поле, индукция которого равна B = 0,1 Тл, вращается с частотой f = 2 об/сек прямоугольная рамка, площадью S = 94 см2. Определить магнитный поток , пронизывающий рамку, когда нормаль к ее плоскости составляет с направлением магнитного поля угол = 45о. Вариант 7. Квадратная рамка площадью S = 120 см2 равномерно вращается в однородном магнитном поле (B = 0,2 Тл) с частотой f = 10 об/сек относительно оси, проходящей в плоскости рамки через середины ее двух противоположных сторон и перпендикулярно линиям индукции. В момент времени t = 0 нормаль к плоскости рамки составляет угол = 0 с линиями поля. Определить три первых момента времени после начала вращения, когда мгновенная э.д.с. в рамке равна = + 0,15 В.