М Е Х А Н И К А
реклама
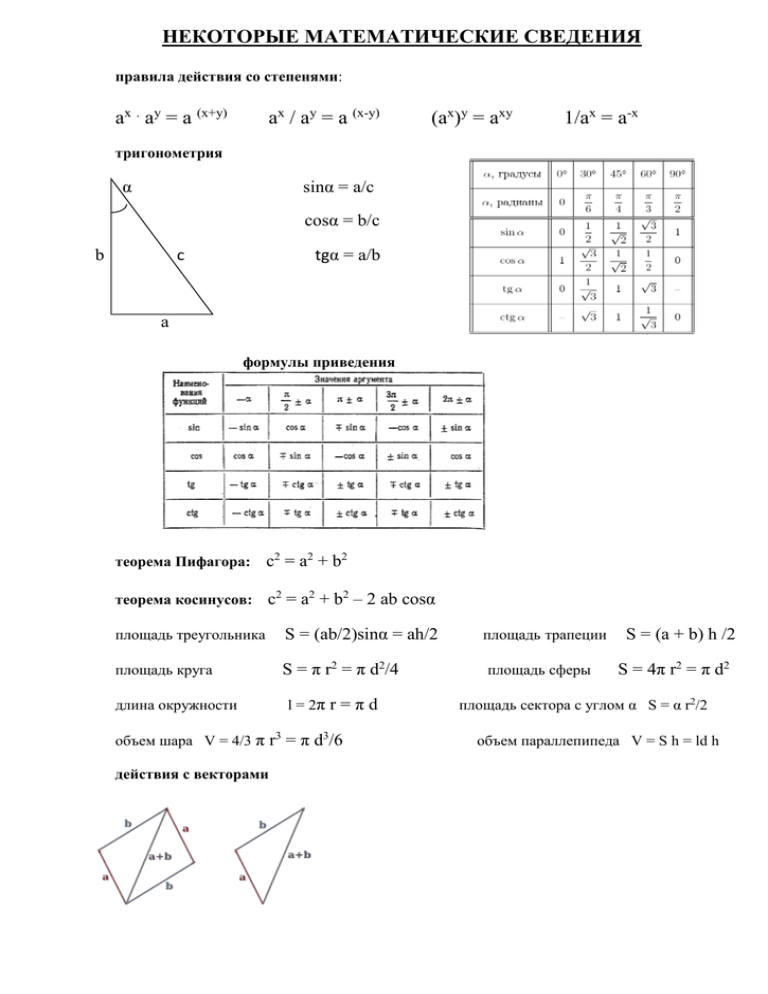
НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ СВЕДЕНИЯ правила действия со степенями: ах . ау = а (х+у) ах / ау = а (х-у) (ах)у = аху 1/ах = а-х тригонометрия α sinα = a/c cosα = b/c b b c tgα = a/b а формулы приведения теорема Пифагора: с2 = а2 + b2 теорема косинусов: с2 = а2 + b2 – 2 аb cosα площадь треугольника S = (ab/2)sinα = ah/2 площадь круга S = π r2 = π d2/4 длина окружности l = 2π r = π d объем шара V = 4/3 π r3 = π d3/6 действия с векторами площадь трапеции площадь сферы S = (a + b) h /2 S = 4π r2 = π d2 площадь сектора с углом α S = α r2/2 объем параллепипеда V = S h = ld h МЕХАНИКА I. КИНЕМАТИКА Физические величины – буквенное обозначение (единицы измерения) Основными единицами измерения являются: кг, м, с. Остальные единицы измерения могут быть выражены через них. Связь основных и составных единиц измерения 1 Н = (кг м)/с2; 1 Дж = (кг м2)/с2 = Н м; 1 Вт = (кг м2)/с3 = Дж/с = (Н м)/с 1 Па = кг/(с2 м) = Н/м2 Координата – х,у (м); пройденный путь(длина) – l (м); перемещение - S (м); высота – h (м) скорость (линейная) – v (м/с); угловая скорость – w (рад/с); ускорение – а (м/с2); время – t (с) ускорение свободного падения – g=9,8 м/с2 период вращения – Т (с); частота вращения – n (с-1); угловая скорость – ω (рад/с) Основная задача механики: определение положения тела относительно других тел в любой момент времени. Система отсчета: тело (точка) отсчета, связанная с ним система координат и часы. Материальная точка: тело, размерами которого в данных условиях можно пренебречь. законы сложения скоростей и перемещений в векторной форме: v = v1 + v2 s = s1 + s 2 где: v - cкорость тела относительно неподвижной системы отсчета (перемещение – s) v1 – cкорость тела относительно подвижной системы отсчета (перемещение – s1) v2 - cкорость подвижной системы отсчета относительно неподвижной системы отсчета (перемещение – s2) кинематические уравнения - это уравнения зависимости x(t); y(t); v(t) уравнение траектории это уравнение y(x) – надо из уравнения x(t) выразить t, подставить это значение в y(t) и получится y(x). средняя скорость – весь путь, деленный на все время: vcp = (l1 + l2 + …) / (t1 + t2 + …) дополнительные формулы для перемещения: s = (v2 – v02)/2a перемещение за n-ую секунду движения: sn = a/2(2 n – 1) Геометрический смысл пройденного пути: перемещение тела за время t определяется по графику зависимости скорости от времени (v(t)) как площадь фигуры ограниченной этим графиком и значением времени. Задачи на движение под действием силы тяжести движение по вертикали: высота h=gt2/2 время полета t=√2ℎ/𝑔 тело брошено с некоторой высоты, скорость направлена горизонтально: высота h=gt2/2 дальность L=v0t время полета тело брошено со скоростью направленной под углом к горизонту: дальность L=(2v02 sinα cosα)/g время подъема: t=(v0 sinα)/g высота h=(vo2 sin2α)/2g время полета: t=(2v0 sinα)/g t=√2ℎ/𝑔 Особенности криволинейного движения: 1. Если точки расположены на одном диске, но на разных расстояниях от центра, то у них одинаковая угловая скорость. 2. Если диски разные, но вращаются вместе (связанные – ременная передача, или соприкасающиеся), то одинаковая линейная скорость. 3. Расчет движения различных точек обода колеса, движущегося по горизонтали со скоростью Vг А По правилу сложения скоростей: точка А: VA = Vг + Vвр или VA = 2Vвр точка В и D: VВ = VD = Vг + Vвр или VВ = VD = Vвр 2 D B точка С: VС = Vг - Vвр или VС = 0 точка О: VО = Vг C Алгоритм решения задач с использованием уравнений движения: 1. Сделать схематичный рисунок с указанием направления скоростей и системой координат 2. Написать общий вид необходимых уравнений движения: x(t), y(t), vx(t), vy(t) 3. Записать начальные и конечные условия (x0, y0, vox, voy, x, y, vx, vy ) 4. Уравнения движения записать с учетом (3) и решить полученные уравнения относительно искомой величины. II. ДИНАМИКА Физические величины – буквенное обозначение (единицы измерения) масса тела – m (кг) плотность – ρ (кг/м3) коэффициент жесткости – k (Н/м); коэффициент трения (сопротивления) - µ сила – F (Н), сила реакции опоры – N (Н), сила натяжения нити – Т (Н), вес тела - Р (Н) правила нахождения проекций векторов Инерция – явление сохранения скорости тела Закон инерции (принцип относительности Галилея): если на тело не действуют другие тела или их действие скомпенсировано, то тело либо покоится, либо движется равномерно и прямолинейно. Инертность – свойство тел сохранять скорость Масса тела – это мера его инертности m=ρV Сила – физическая величина, характеризующая взаимодействие тел и являющаяся причиной ускорения. Результирующая (равнодействующая) сила – векторная сумма всех сил, действующих на тело. Fрез = F1 +… + FN 1-й закон Ньютона: Существуют такие системы отсчета (инерциальные), относительно которых, тело, на которое не действуют другие тела или их действие скомпенсировано (Fрез =0) покоится или движется равномерно и прямолинейно. Инерциальные системы – это неподвижные или движущиеся равномерно и прямолинейно системы отсчета 2-й закон Ньютона: Результирующая сила (векторная сумма всех сил действующих на тело) равна произведению массы тела на сообщаемое этой силой ускорение. Fрез = ma; F ↑↑ a 3-й закон Ньютона: Сила действия равна противодействию. F12 = - F21 Силы приложены к разным телам. Пример: сила реакции опоры (нормального давления) и вес тела. Сила Всемирного тяготении: сила тяжести Fтяж = mg F = GMm/R2 ускорение свободного падения при 1-я космическая скорость и скорость полета спутника h≪R g = GM/R2 vI =√𝐺𝑀/𝑅 = √𝑔𝑅 ; vII = vI √2 Для Земли vI = 7,9 км/с; vII = 11 км/с Вес тела: а = о, Р = mg а↑↑g, P = m(g – a) a↑↓g, P = m(g + a) Невесомость – вес равен 0, свободное падение: а = g Частным случаем сил упругости являются сила натяжения нити частный случай силы упругости: сила натяжения нити (Т) и сила реакции опоры или нормального давления (N) Сила трения – сила возникающая между соприкасающимися телами и направленная против возможного движения Fтр = µN (для движения по горизонтали Fтр = µmg ) Алгоритм решения задач на динамику: 1. Сделать рисунок, где изобразить все силы, действующие на тело или несколько тел. 2. Выбрать и начертить систему отсчета (иногда для нескольких тел, например для связанных тел). 3. Записать для данной задачи 2-й закон Ньютона в векторной форме для каждого тела. 4. Переписать (3) в проекциях на оси координат и с учетом данных задачи. 5. Полученные уравнения решить относительно искомой величины. III. СТАТИКА Точка опоры(точка вращения) – точка, относительно которой может вращаться тело. Плечо силы – кратчайшее расстояние от точки вращения до линии действия силы – d (м) Момент силы – произведение силы на ее плечо – М (Нм) Если сила вращает тело по часовой стрелке, то М>0, если протии часовой стрелки, М<0 Условия равновесия: 1) Векторная сумма всех сил, действующих на тело, равна 0. 𝛴Fi = 0 2) Cумма моментов всех сил равна 0. 𝛴 Мi = 0 «Золотое» правило механики: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии – ни один из механизмов не дает выигрыша в работе. Если в сообщающихся сосудах налиты неоднородные жидкости, то чем больше плотность жидкости, тем меньше высота столба этой жидкости в колене сообщающегося сосуда. При движении жидкости (газа) по трубам разной толщины – действует следующее правило (закон Бернулли): чем толще труба (больше площадь поперечного сечения), тем меньше скорость и больше давление, отсюда и возникает подъемная сила крыла. IV. ЗАКОНЫ СОХРАНЕНИЯ Физические величины – буквенное обозначение (единицы измерения) работа – А (Дж); энергия – Е (Дж); мощность – N (Вт); коэффициент полезного действия КПД – η (%) импульс тела – р (кг м/с) Импульс силы – произведение силы на время ее действия (F t). Импульс силы равен изменению импульса тела Ft=∆p Механическая работа: A = Fs cosα Работа силы тяжести Работа силы упругости Работа результирующей силы A(Fтяж) = - ∆Ep A(Fупр) = - ∆Ep A(Fрез) = ∆Eк если действуют силы сопротивления, то или Ер2 + Ек2 = Ер1 + Ек1 + Q A(Fтр) = - ∆Eп = - ((Ер2 + Ек2) - (Ер1 + Ек1)) = Q (где Q – выделившееся в результате трения количество теплоты) Алгоритм решения задач на законы сохранения: 1. Записать закон сохранения (изменения) энергии (импульса) в общем виде. 2. Определить начальную и конечную энергию (импульс) тела. 3. Записать (1) с учетом (2) (и проекций для импульса). 4. Решить полученные уравнения относительно искомой величины. V. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ Вынужденные колебания – колебания, происходящие под действием периодически изменяющейся внешней силы. Резонанс – резкое возрастание амплитуды колебаний при совпадение частоты внешней силы и собственной частоты колебаний. Звук – механическая продольная волна. Распространяется только в веществе, чем плотнее вещество, тем больше скорость звука в нем. Высота тона звука зависит от частоты колебаний источника звука Громкость звука зависит от амплитуды колебаний источника звука


