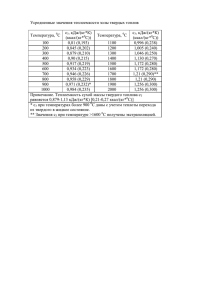
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ ЯРОСЛАВА МУДРОГО
Самолюк Н.П.
ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ МЕТАЛЛОВ МЕТОДОМ
ОХЛАЖДЕНИЯ
Учебно–методическое пособие по лабораторной работе для студентов
физико-математических и инженерных специальностей
ВЕЛИКИЙ НОВГОРОД
2011
2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ ЯРОСЛАВА МУДРОГО
Самолюк Н.П.
ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ МЕТАЛЛОВ МЕТОДОМ
ОХЛАЖДЕНИЯ
Учебно–методическое пособие по лабораторной работе для студентов
физико-математических и инженерных специальностей
ВЕЛИКИЙ НОВГОРОД
2011
3
УДК 53 (0765)
Рецензент: кандидат физико-математических наук, доцент Иванова
Г.Я.
В пособии подробно рассмотрены теоретические положения,
необходимые для выполнения лабораторной работы, а также порядок
выполнения лабораторной работы. Пособие может быть использовано
на всех специальностях, в стандарты которых включена дисциплина
«Физика»
Определение теплоемкости металлов методом охлаждения. Учебно–методическое
пособие
по
лабораторной
работе
для
студентов
физико-
математических и инженерных специальностей. / Сост. Н.П. Самолюк. НовГУ им. Ярослава Мудрого. – Новгород, 2011. – 25 с.
4
ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ МЕТАЛЛОВ МЕТОДОМ
ОХЛАЖДЕНИЯ
Лабораторная работа
Цель работы: 1. Изучить закон Дюлонга и Пти;
2. Изучить модель Дебая для вычисления теплоемкости твердого тела;
3. Измерить удельную теплоемкость твердых тел методом охлаждения.
Приборы и оборудование: печь; термопара; милливольтметр; штатив;
подставка для установки образцов; градуировочный график; набор
образцов из исследуемых металлов; секундомер; источник тока.
1. Теория вопроса. Модель Дебая
В молекулярной физике понятие теплоемкости играет важную роль.
Это связано с тем, что теплоемкость является не только характеристикой
процесса, но и характеристикой вещества. Это говорит о том, что
теплоемкость
определяется
строением
вещества
и
особенностями
теплового хаотического движения частиц, из которых состоит вещество.
Поэтому, зная теплоемкость вещества, можно делать выводы о строении
вещества и о поведении частиц вещества.
На основе распределения Максвелла была выведена теорема о
равномерном распределении энергии по степеням свободы, на основе
которой была сформулирована классическая теория теплоемкостей
идеальных газов. Согласно теореме о равномерном распределении энергии
по степеням свободы, на каждую степень свободы поступательного и
вращательного движения молекулы приходится в среднем одинаковая
энергия, равная
1
k  T , то есть:
2
1
2
 nocm 1   bp   k  T
1
(1)
5
Согласно
этой
же
теореме,
на
каждую
степень
свободы
колебательного движения молекулы приходится в среднем одинаковая
энергия, равная k  T :
 koл 1  k  T
(2)
Из этой теории следует, что теплоемкость газов зависит только от
геометрии молекул газа, которая позволяет определить число степеней
свободы вращательного и колебательного движений. По классической
теории теплоемкостей газов получается, что теплоемкость газов не зависит
от рода газа и не зависит от температуры.
Сравнение этой теории теплоемкостей с экспериментом показало,
что эта теория хорошо согласуется с экспериментом только при высоких
температурах, а при низких температурах наблюдается существенное
расхождение теоретических и экспериментальных результатов. Для
объяснения этих расхождений в классической физике было введено
понятие
о
«замораживании»
степеней
свободы.
Согласно
этому
представлению, молекулы газа при средних и низких температурах не
совершают колебательного движения. Для легкого газа, например для
водорода,
при
низкой
температуре
молекулы
не
участвуют
во
вращательном движении.
Классическая физика не могла объяснить замораживание степеней
свободы. Это удалось сделать только на основе квантовых представлений,
согласно которым энергия колебательного движения атомов в молекулах
может принимать только дискретные значения.
При определении теплоемкости твердых тел Дюлонг и Пти
использовали классическую теорему о равномерном распределении
энергии по степеням свободы. При этом необходимо учитывать, что
атомы, ионы или другие структурные элементы, находящиеся в узлах
кристаллической
решетки
твердого
тела,
совершают
хаотические
колебательные движения около положения равновесия. Все возможные
6
колебания можно разложит по трем осям неподвижной системы координат
и тогда получается, что каждый структурный элемент кристаллической
решетки совершает хаотические колебания по трем независимым
направлениям, а это означает, что каждый структурный элемент имеет три
степени свободы колебательного движения.
Так как по теореме о равномерном распределении энергии по
степеням свободы, на каждую степень свободы колебательного движения
приходится в среднем одинаковая энергия, равная k  T , то каждый
структурный элемент кристаллической решетки твердого тела имеет
среднюю энергию хаотического движения, равную 3  k  T :
  3 k T
(3)
Тогда внутренняя энергия одного моля твердого тела будет равна:
U  NA    3 NA  k T  3 R T
(4)
При записи формулы (4) использовался постулат термодинамики,
согласно которому все термодинамические величины определяются
средними
значениями
соответствующих
отдельные частицы. В формуле (4)
N A  6,02  1023
k
величин,
характеризующих
- постоянная Больцмана,
1
Дж
- число Авогадро, R  8,31
- универсальная
моль
моль  К
газовая постоянная, T - температура.
Используя формулу (4), можно найти молярную теплоемкость
твердого тела в процессах при постоянном объеме:
 U 
CV  
  3 R
 T V
(5)
Формула (5) называется законом Дюлонга и Пти. Согласно этой
7
формуле теплоемкость твердых тел не зависит от температуры и не
зависит от рода вещества. Сравнение этого закона с экспериментальными
данными показало, что классическая теория теплоемкостей дает хорошее
согласие с экспериментом только при высоких температурах. При низких
температурах наблюдается существенное расхождение теоретических и
экспериментальных результатов.
Для того, чтобы преодолеть различия экспериментальных и
теоретических результатов, Эйнштейн предложил квантовую теорию
теплоемкостей. Он рассматривал каждое колебательное движение в
кристалле как независимое от других колебаний и описывал его как
квантовый гармонический осциллятор. В модели Эйнштейна атомы в узлах
кристаллической решетки твердого тела могут колебаться с различными
частотами, величина которых может изменяться от нуля до бесконечности.
В результате для теплоемкости твердого тела была получена
следующая формула:
 h  
 h  
3 NA  k 
 exp 


 U 
 k T 
 k T 
CV  


2
 T V

 h   
 exp  k  T   1

 

2
(6)
Здесь h  6,63 1034 Дж  с - постоянная Планка,  - частота колебаний
структурного элемента твердого тела.
Из формулы (6) следует, что теплоемкость твердого тела зависит от
температуры и от частоты колебаний атомов твердого тела. Чтобы
сравнить результаты этой теории с экспериментом рассмотрим, как
выглядит эта функция при малых и при больших температурах.
Проанализируем модель Эйнштейна при больших температурах. В
этом
случае
h 
 1 ,
k T
разложить в ряд:
тогда
экспоненциальную
функцию можно
8
h 
 h  
exp 
 1
k T
 k T 
(7)
Подставляем формулу (7) в формулу (6) и получаем:
h  

1


k T 
 h  

CV  3  R  
 3 R
 
2
 k T  
h 

 1
1 
 k T

2
(8)
Формула (8) показывает, что при высоких температурах модель
Эйнштейна дает результат, совпадающий с классическим законом
Дюлонга и Пти, который дает хорошее совпадение с экспериментом при
этих условиях. Переход результата квантовой теории в предельном случае
к результату классической теории свидетельствует о выполнении одного
из главных признаков научного знания, который называется принципом
соответствия. Согласно этому принципу, новая более точная наука не
отбрасывает результаты менее точной науки, а содержит их как
предельный случай. Дальнейшее развитие теории теплоемкостей твердых
тел состоит в том, чтобы получить совпадение с экспериментом при
низких температурах.
При малых температурах T  0 , тогда
h 
 1 , следовательно
k T
 h  
exp 
  1. Это значит, что единицей в знаменателе формулы (6)
 k T 
можно пренебречь. Тогда получаем, что при низких температурах
теплоемкость твердого тела имеет вид:
 h  
 h  
CV  3  R  
  exp  

 k T 
 k T 
2
(9)
Сравнение этой формулы с результатами эксперимента показывает,
что при низких температурах модель Эйнштейна не применима, так как на
9
опыте показано, что при низких температурах теплоемкость твердого тела
растет пропорционально третьей степени температуры, то есть имеет вид
CV    T 3
(10)
где   const . Этот закон был получен в модели, предложенной Дебаем и
поэтому формула (8) называется законом Дебая.
В модели Дебая учитывается, что колебания атомов в кристалле
приводят к тому, что в кристалле, как и в любой другой упругой среде
возникает
система
стоячих
волн,
аналогичных
стоячим
волнам,
возникающим в струнах, стержнях. При изучении стоячих волн в механике
было показано, что уравнение стоячей волны, распространяющейся в
одном направлении, например, вдоль оси OX имеет вид:
  x, t   A  sin  k x  x   cos t
Здесь A - амплитуда волны, k x 
2

(11)
- волновой вектор, направленный
вдоль оси OX ,  - длина волны, x - координата точки среды, в которой
распространяется волна,  
2
T
- циклическая частота, T - период
колебаний частиц в волне.
Если волна распространяется в любом направлении, то формула (11)
для такого случая будет иметь вид:
  x, y, z, t   A  sin  k x x   sin  k y y   sin  k z z   cos t 
(12)
Здесь k x , k y , k z - проекция волнового вектора на координатные оси.
Из механики стоячих волн также известно, что в ограниченном
стержне распространяются только такие стоячие волны, для которых
волновой вектор k x принимает значения, удовлетворяющие условию:
kx 
n
(13)
l
Здесь n  1,2,3,... , а l - длина стержня, вдоль которого распространяется
волна.
Формула
(13)
справедлива
для
случая,
когда
волна
10
распространяется в одном направлении. Эти представления можно
обобщить на случай, когда в твердом теле волны распространяются по
трем независимым направлениям. Для этого рассмотрим кристалл в форме
прямоугольного параллелепипеда со сторонами a, b, c . Такой кристалл
изображен на рисунке 1.
Рис.1. Кристалл в форме прямоугольного параллелепипеда.
Упругая волна в таком кристалле описывается формулой (12), в
которой проекции волнового вектора на координатные оси подчиняются
условиям:
kx 
 n1
a
;ky 
 n2
b
; kz 
 n3
(14)
c
где n1, n2 , n3  1,2,3,....
Найдем число dN k упругих стоячих волн в кристалле, для которых
модуль волнового вектора принимает значения в интервале  k ; k  dk  . Все
эти векторы заканчиваются внутри восьмой части сферического слоя,
радиус которого равен k , а толщина равна dk . Эта ситуация наглядно
представлена на рисунке 2.
На
каждый
вектор
k,
координаты
которого
определяются
формулами (14) приходится объем, который определяется по формуле:
  
3
3
  

,
a b c abc V
где V  abc - объем рассматриваемого кристалла.
(15)
11
Рис.2. Геометрическая иллюстрация к вычислению числа dN k упругих
волн в кристалле, имеющем форму прямоугольного параллелепипеда.
Объем выделенной части сферического слоя вычисляется по
формуле:
1
dVk   4  k 2  dk
8
(16)
Тогда число упругих волн можно определить, разделив объем выделенной
части сферического слоя (16), на объем, приходящийся на каждый
волновой вектор (15). Однако необходимо учесть, что в твердом теле в
одном направлении может распространяться две поперечных волны и одна
продольная волна, поэтому полученное при делении число необходимо
умножить на три, то есть на полное число волн, которые соответствуют
одному волновому вектору в твердом теле. Тогда число упругих волн
будет определяться по формуле:
3  V  k 2dk
dN k 
2 2
(17)
Из определения волнового вектора следует:
k
2


2  2
 
,
c T c
c
(18)
где c - скорость распространения волн,  - частота колебаний частиц в
волне.
По формуле (18) определяем:
12
dk 
d 2 d

c
c
(19)
Подставляем формулы (18) и (19) в формулу (17) и получаем число
волн, для которых частоты лежат в интервале  ,  d  , равно:
3  V   2  d
dN 
2 2  c3
(20)
Так как полное число колебаний в твердом теле равно 3N , тогда
выполняется условие:
 dN  3N
(21)
 
Если формулу (20) подставить в формулу (21), то станет понятно, что
интеграл будет сходиться, если частота колебаний атомов в твердом теле
не превышает некоторого максимального предельного значения max :
  max . С учетом этого условия получаем:
3 V
2 2  c3
max

 2  d  3N
(22)
0
Из формулы (22) найдем значение max :
max  3
Здесь n 
6 N   2  c3
 c  3 6 2  n
V
(23)
N
- концентрация атомов в твердом теле.
V
При изучении квантового гармонического осциллятора получено,
что средняя энергия одного гармонического осциллятора определяется
выражением:
 
h 
h
e kT
1

h 
2
(24)
Если предположить, что средняя энергия одной упругой волны в
кристалле равна средней энергии квантового гармонического осциллятора,
тогда внутренняя энергия кристалла будет определяться по формуле:
13
U
max

0
3 V
  ddN  2 3
2  c
max 

0

         2 d
 
2 
k

T
 e 1

(25)
В формуле (25) использовано известное в физике обозначение

h
. Интеграл (25) будем вычислять как сумму интегралов. Сначала
2
рассмотрим второй интеграл, который представляет собой энергию
нулевых колебаний U 0 . Особенность ее состоит в том, что она не зависит
от температуры и, следовательно, не может вносить вклад в теплоемкость
кристалла.
3 V
U0  2 3 
2  c 2

max

4
3  V  max
  d  2 3 
4
4  c
3
0
(26)
3 V 
9
3
2

c

6


n



  max  N
max
8
16 2  c3
Вычислим первое слагаемое в формуле (25):
3 V
U1 T   2 3
2  c
max



0
e kT
  2  d
(27)
1
Для того чтобы вычислить этот интеграл, введем новую переменную
x

kT
kT
; 
 x; d 
 dx
kT
(28)
Подставляем формулы (28) в формулу (27):
3 V 
U1 T   2 3
2  c

3  V   kT 


2 2  c3 

xmax

4
3
 kT  x  dx


 x

 e 1
0
4 xmax

0
x  dx
3 V  k

e x  1 2 2  c3 
3
4
T 4
3
xmax

0
(29)
x  dx
ex  1
3
Полная внутренняя энергия кристалла определяется суммой энергии
нулевых колебаний U 0 и энергии U1 T  . Однако, так как от температуры
зависит только
U1 T  , то при определении теплоемкости будем
рассматривать только эту часть внутренней энергии твердого тела.
14
Чтобы найти теплоемкость твердого тела, надо по определению
теплоемкости
продифференцировать
последнее
выражение
по
температуре. При этом получим, что теплоемкость твердого тела является
функцией температуры и зависит от рода вещества. Зависимость от рода
вещества связана с тем, что в формуле внутренней энергии присутствует
максимальная частота колебаний, которая для различных твердых тел
будет принимать различные значения.
Рассмотрим
поведение
внутренней
температурах, то есть при условии
энергии
при
низких

 1 . Тогда значение xmax будет
kT
очень велико, и его можно считать равным бесконечности. Тогда интеграл
можно вычислить в явном виде:

x3  dx  4
 e x  1  15
0
(30)
Теперь при низких температурах имеем:

3
4
3 V  k 4
3 V  k 4
 2 V  k 4 4
4 x  dx
4 
U1 T   2 3 3  T  x
 2 3 3 T 

 T (31)
3
3
15
2  c 
e

1
2


c

10

c

0
По определению находим теплоемкость твердого тела при низких
температурах:
 2 V  k 4
2 2  V  k 4 3
 U 
3
CV T   
 4 T 
T   T 3
 
3
3
3
3
5c 
 T V 10  c 
(32)
Из последней формулы следует, что теплоемкость твердого тела при
низких температурах пропорциональна третьей степени температуры, что
соответствует опытным наблюдениям.
Используя формулу (23) для максимальной циклической частоты,
можно изменить вид постоянной  в формуле (32). При этом получаем:
2 2  V  k 4 2 2  V  k 4  6 2  N 12 4  N  k 4




3
3
5  c3  3
5  max
 3 V
5  max
 3

12  N  k  k 


5
  max 
4
3
(33)
15
Подставляем формулу (33) в (32) и получаем:
3
4

k
 U 
3 12  N  k 
3
CV T   

 T 
   T 
5
 T V
  max 

3
12  N  k  k  T  12  N  k  T 

 
 
5


5
 
max 

4
4
(34)
3
В формуле (34) введено удобное обозначение  
 max
(35). Эта
k
величина называется температурой Дебая.
При высоких энергиях в формуле (29) для внутренней энергии
кристалла величина x 

 1 . Поэтому экспоненту можно разложить в
kT
ряд Тейлора и ограничиться двумя членами разложения: e x  1  x . Тогда
исследуемая часть внутренней энергии кристалла будет иметь вид:
U1 T  
3 V  k
2 2  c3 
4
3 V  k 4
 2 3 3 T 4
2  c 
T 4
3
xmax

0
xmax

0
x  dx
3 V  k

e x  1 2 2  c3 
3
4
3
T 4
xmax

x3  dx

1 x 1
0
3
3 V  k 4
4 xmax
x  dx  2 3 3  T 

3
2  c 
2
(36)
3
3
 max
V  k4
4
 2 3 3 T  3 3 
2  c 
k T
3
V k
c  6 2  N
 2 3 T 
 3 N  k T
V
2  c 
Тогда при высоких температурах для теплоемкости твердых тел
получаем:
 U 
CV  
  3 N  k
 T V
Если число частиц твердого тела равно числу Авогадро, то молярная
теплоемкость твердого тела при высоких температурах определяется по
формуле:
 U 
CV , моль  
 3 NA  k  3 R T

 T V , моль
(37)
16
Эта формула соответствует классическим представлениям и выражает
известный закон Дюлонга и Пти. Таким образом, модель Дебая наиболее
точно описывает теплоемкость твердых тел.
2. Теоретические основы метода измерения
Возьмем металлический образец произвольной формы. Если в
качестве начала отсчета температур принять температуру окружающей
среды, то количество тепла, отдаваемое телом за единицу времени его
поверхностью S , будет равно:
q   TnobdS
(1)
S
Здесь  - коэффициент теплоотдача, который зависит не только от
температуры поверхности тела Tnob при известной температуре окружающей
среды, но и от значения градиента температуры в окружающей среде вблизи
поверхности образца. В соответствии с этим внутренняя энергия тела за единицу
времени уменьшается на величину:
q    c
V
T
dV ,
t
(2)
где c - удельная теплоемкость вещества,  - плотность вещества, V - объем
тела.
По закону сохранения энергии эти количества теплоты должны быть
равны друг другу. Следовательно:
 c
V
T
dV      Tnob  dS
t
S
(3)
Умножим и разделим левую часть равенства (3) на величину объема, а
правую часть - на величину поверхности. Получим:
V
1
T
1
c

dV


S
  Tnob  dS
V V
t
S S
(4)
Принимая c и  в качестве средних значений удельной теплоемкости и
плотности по объему, а величину  в качестве среднего значения коэффициента
17
теплоотдачи по поверхности и вынося их за знаки интегралов, получим:
Vcp  c   
1 T
1
  dV   S      Tnob  dS
V V t
S S
1 T

 dV
V V t
Величина
представляет
собой
(5)
среднее
значение
скорости охлаждения объема тела. Тогда для краткости можно ввести
обозначение:
1 T
T

 dV 
V V t
t
В свою очередь величина
(6)
1
 Tnob  dS представляет собою среднее
S S
значение температуры поверхности, и для нее можно ввести обозначение:
1
 Tnob  dS  Tnob
S S
(7)
Таким образом, выражение (5) с учетом обозначений (6) и (7)
принимает вид:
Vcp  c   
T
   S  Tnob
t
(8)
Так как объем, по которому производилось интегрирование, со временем
не меняется, то можно считать, что:
T


T
t
t
(9)
и тогда выражение (8) принимает вид:
Vcp  c   
 T
   S  Tnob
t
(10)
Возьмем теперь два образца из различных металлов. Запишем выражение
(10) для каждого из этих образцов, употребляя для параметров одного из них
индекс 1, а для другого индекс 2:
18
 T 
V1  c1  1  
    S1  Tnob

t

1
1
 T 
V2  c2   2  
    S 2  Tnob
 t 2
(11)
2
Если оба образца при комнатной температуре имеют одинаковые
объемы и одинаковую форму, то V01  V02 , а также S01  S02 .
Примем во внимание далее, что всегда
V01  01  m1  V1  1 , а также V02  02  m2  V2  2 ,
где m1 - масса первого образца, m2 - масса второго образца. Из отношения
правых и левых частей уравнений (11) получим:
 T

m2  t
c1  c2 

m1   T

 t


2 1  Tnob

  2  Tnob

1
1
,
(12)
2
где c2 - известная удельная теплоемкость одного из образцов.
Если взять образцы в форме тонкого цилиндра, то, пренебрегая влиянием
концов, можно будет считать тепловой поток направленным по радиусам
цилиндра от оси к поверхности. В этом случае средняя температура поверхности
будет просто температурой боковой поверхности. Измерить температуру
поверхности или среднюю температуру по объему трудно, значительно легче
измерить температуру на оси цилиндра (например, термопарой). Но при этом
возникает совершенно законный вопрос о том, какова будет ошибка при замене
температуры поверхности температурой, измеренной на оси образца.
В работе 9 был рассмотрен вольфрамовый образец радиусом 0,3 см.
Уравнение теплопроводности в цилиндрических координатах имеет вид:
2
T   T
2  T 
c 
 
r  2 
t r  r
r 
(13)
где  - коэффициент теплопроводности вольфрама. Как и в случае
определения средней температуры на поверхности, мы опять не принимаем во
19
внимание влияния концов образца, поэтому в уравнении (13) отсутствует
вторая производная по координате z .
Решение этого уравнения получено в работе [9], для тонкого (длинного)
цилиндра при начальных условиях:
t  0, Tnob  const ,
(14)
и при граничном условии:
 T 
    Tnob
 r  nob
 
Для
теплоотдачи
температуры
равен
(15)
поверхности
Tnob  10000 C
коэффициент
кал
.
см  с 0 С
Коэффициент
приблизительно 0,3  102
2
теплопроводности вольфрама равен приблизительно 0,3
кал
. Из
см  с 0 С
2
граничного условия (15) следует:

0,3  10
 T 

    Tnob  

0,3
 r nob
2
 10  10
3
0
C
см
(1кал = 4,1868Дж).
В предположении линейной зависимости T  r  в объеме образца
0
T   Tnob
C
можно записать:
. Тогда разность температур T   Tnob при
 10
r
см
радиусе образца r  0,3см составит T   Tnob  30 C . В действительности
линейного распределения температуры по радиусу нет. Истинное значение
температуры на оси цилиндра гораздо меньше, чем T  .
Таким образом, если
вместо
температуры
поверхности
взять
преувеличенное значение температуры на оси цилиндра, то ошибка
составляет  30 C .
Если температуру T  приравнять температуре T , действительно
измеренной на оси образца, то ошибка будет гораздо меньше 30 C . Тогда
для измерения теплоемкости при 10000С относительная ошибка составит,
гораздо меньше, чем 0,3 %. В действительности относительная погрешность
20
при измерении теплоемкости значительно больше  2  3%  .
Что же касается средней температуры по объему, то ее величина еще
меньше отличается от температуры на оси цилиндра, и поэтому при замене
средней температуры по объему температурой на оси будет допущена еще
меньшая ошибка.
Существенно отметить, что эти обе ошибки действуют в разные
стороны: если первая при замене температуры поверхности температурой на
оси - в сторону увеличения результата, то вторая - при замене температуры
средней по объему температурой на оси - в сторону уменьшения результата.
При более низких температурах, при которых коэффициент теплоотдачи
меньше, ошибки также будут меньшими.
Таким образом, можно считать достаточно обоснованной замену
температуры средней по объему и температуры на поверхности температурой
на оси цилиндра, которая измеряется в эксперименте. С учетом проведенных
оценок выражение (12) приобретает вид:
 T 


m2  t 2 1  T1
c1  c2 


m1  T   2  T2


 t 1
(16)
Практически можно для расчетов брать образцы в таких состояниях,
когда их температуры одинаковы; но при условии Tnob1  Tnob 2 или, вследствие
вышеуказанной замены, при T1  T2 , также 1   2 .
При этом предполагается, что условия охлаждения для обоих образцов
совершенно одинаковы, тогда вместо (16) можно записать:
 T 


m2  t 2
c1  c2 

m1  T 


 t 1
Таким
образом,
если
(17)
один
образец
изготовить
из
металла,
теплоемкость которого c2 достаточно точно определена в зависимости от
21
температуры, и использовать этот образец в качестве эталона, то можно
получить температурную зависимость теплоемкости другого образца.
Так как длительность эксперимента не может превышать времени,
необходимого на охлаждение образца, то опытная часть определения
температурной зависимости теплоемкости металла потребует мало времени,
что имеет существенное значение в условиях студенческого физического
практикума.
3 Описание установки и метода измерения
Схема установки изображена на рис.1. Электропечь A смонтирована на
направляющем стержне, по которому она может перемещать, вверх и вниз.
Образец B представляет собой цилиндр высотой 30 мм и диаметром 5 мм с
высверленным с одного конца каналом. Этим каналом образец помещают на
фарфоровую трубку, через которую пропущены концы, термопары C .
Температура образца отсчитывается с помощью
милливольтметра,
снабженного графиком перевода его показаний в значения температуры
спая термопары. В начале опыта электропечь опускают по направляющему
стержню вниз настолько, чтобы образец полностью оказался внутри нее, и
включают источник тока. После нагрева образца до
температуры
~550+600°С печь отключают от источника тока, быстро поднимают вверх и
закрепляют винтом. Нагретый образец охлаждается в неподвижном воздухе.
С помощью секундомера через каждые 10 производят запись показаний
милливольтметра, и по графику определяют температуру образца. После
охлаждения образца до температуры ниже 100 0С опыт повторяют.
Для каждого образца необходимо снять две кривые охлаждения. Кривые
получают для трех образцов: медного, алюминиевого и железного. За эталон
принимается образец из меда, для которого зависимость теплоемкости от
температуры приведена в таблице 1.
Таблица 1. Зависимость удельной теплоемкости меди от температуры
600
0,1090
400 500
0,1070
300
0,1038
200
0,1008
Теплоемкость меди,
100
0,0975
0
0,0940
Температура, 0С
0,0910
22
Рис. 1. Схема установки для нагревания образцов и измерения
температуры
Полученные
в
опыте
кривые
T  f t  ,
дающие
зависимость
температуры от времени для трех образцов, необходимо перевести в кривые
T
. С этой целью кривые T  f  t  разбиваются на участки достаточно
t
близкими друг к другу вертикальными линиями, проведенными на
одинаковом расстоянии. Эти линии представляют собой линии одинаковых
температур, т. е. изотермы. Интервал между изотермами можно принять
равным 25 °С. В этом случае отношение скоростей охлаждения определяется
только
промежутками
времени.
Отношение
скоростей
охлаждения,
определенное этим способом, относится к средней температуре между
изотермами. Ошибки здесь появляются, главным образом, за счет измерения
интервалов времени.
Можно, наоборот, выделить на кривых участки, соответствующие
одинаковым интервалам времени. Тогда отношение скоростей охлаждения
будет определено через отношение разностей температур на концах
23
выделенных участков кривых. Ошибки при этом появляются, главным
образом, за счет измерения этих разностей температур.
Оба эти способа равноценны и дают для каждой кривой средние
значения скоростей охлаждения по отношению к выделенным интервалам
температур. Подставляя полученные отношения скоростей охлаждения в
формулу (17), получают зависимость теплоемкости от температуры
c   T  для каждого образца, массы которых определяют взвешиванием.
Порядок выполнения работы и обработки результатов измерений
продумайте самостоятельно.
4. Контрольные вопросы
1. Какая физическая величина называется теплоемкостью?
2. Какова связь между молярной и удельной теплоемкостями вещества?
3. Какова связь между молярными теплоемкостями вещества в изохорном
и изобарном процессах в идеальных газах?
4. Какова схема установки для определения теплоемкости методом
охлаждения?
5. Каков порядок выполнения работы?
6. Как получить кривую охлаждения образца?
Каким образом из зависимости
7.
охлаждения
8.
9
T  f t 
найти скорость
T
образца в заданных интервалах температур?
t
Что называется коэффициентом теплоотдачи? От чего он зависит?
Получить дифференциальное уравнение теплопроводности в случае
цилиндрической симметрии задачи.
10.Получить рабочую формулу для расчета удельной теплоемкости
твердого тела методом охлаждения.
11.Каковы погрешности измерения при определении теплоемкости
методом охлаждения?
12.Каковы основные положения классической теории теплоемкости
24
твердых тел и ее выводы?
13.Какие закономерности были установлены при экспериментальных
следованиях теплоемкости твердых тел?
14.Теплоемкость кристаллической решетки в модели Эйнштейна.
Частные случаи.
15.Теплоемкость кристаллической решетки в модели Дебая. Частные
случаи.
16.Сравнение
выводов
теория
Эйнштейна
и
Дебая
с
экспериментальными результатами.
17.Что такое характеристическая температура? От чего она зависит?
5. Техника безопасности
Будьте осторожны при работе с электрической печкой.
Тело переносите из нагревателя в калориметр только с помощью
щипцов. Температура тела больше 100 0С.
6. Литература
1. Б.В.Бондарев, Н.П.Калашников, Г.Г.Спирин. Курс общей физики. Книга
3. Термодинамика. Статистическая физика, Строение вещества: - М.:
Высшая школа, 2003. – 366 с.
1. И. К. Кикоин, А. К. Кикоин. Молекулярная физика. Лань, 2008 г. – 484 с.
2. А. А Детлаф., Б.М. Яворский Курс физики. Учеб. пособие для студ.
втузов – М.: Издательский центр «Академия», 2003. – 720 с.
3. С.Э. Фриш, А.В. Тиморева. Курс общей физики. В 3 томах. Том 1.
Физические основы механики. Молекулярная физика. Колебания и волны.
Лань, 2007. – 480 с.
4. Т.И. Трофимова. Курс физики. Учебное пособие – М.: Издательский
центр «Академия», 2007. – 560 с.
5. Д. В. Сивухин. Общий курс физики. Том 2. Термодинамика и
молекулярная физика. Физматлит/МФТИ, 2005. – 544 с.
25
6. А.Н. Матвеев. Молекулярная физика. Издательство: Лань, 2010. – 368 с
7. С.Е. Мальханов. Общая физика - Конспект лекций. Издательство: СанктПетербург, 2001. – 438 с.
8. А.Н. Зайдель. Ошибки измерений физических величин: учеб. пособие.
Издательство: Лань СПб, 2005. – 112 с.
9. Я.А. Tуровский, Г.М. Бартенев. Определение теплоемкости металлов
методом охлаждения // ЖТФ. - 1940. - Т.10, вып. 6. - С. 514 - 524.
10. О.М. Тодес, Г.А. Зисман. Курс общей физики: В 3 тт: Т. 1: Механика;
Молекулярная физика; Колебания и волны. Издательство Лань, СПб,
2007.-352 с.
11. Курс общей физики: Молекулярная физика /Е.М. Гершензон, Н.Н.Малов и
др. - М.: Просвещение, 1982. - С. 162 -169.
12. В. Ф. Яковлев. Курс физики: Теплота и молекулярная физика. - М.:
Просвещение, 1976. - С. 262 - 265.
13. Г.И. Епифанов. Физика твердого тела. - М.: Высшая школа, 1977 - С. 89 –
103.
14. Ч. Киттель. Введение в физику твердого тела. - М.: Наука, 1978. - С.
211-230.
15. Г.С. Жданов. Физика твердого тела. - М.: МГУ, 1962. - С 378 – 381,
С 387-388.
16. Р. В. Телеснин. Молекулярная физика Издательство: Лань, 2009.- 368 с.
Содержание
Стр.
1. Теория вопроса. Модель Дебая
4
2. Теоретические основы метода измерения
3 Описание установки и метода измерения
16
21
4. Контрольные вопросы
5. Техника безопасности
23
24
6. Литература
24