Задачи на движение - Образовательный портал г. Липецка
реклама

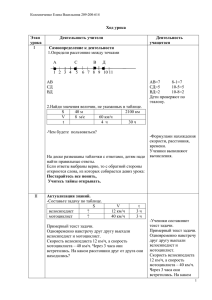
Никонович Елена Васильевна учитель начальных классов МОУ лицей №44 Урок математики в 4 классе. Образовательная система «Школа 2100». Тема урока: «Задачи на движение». Цели урока: Образовательные: обобщать и систематизировать знания о различных видах движения: навстречу друг другу, в противоположных направлениях, вдогонку, с отставанием; отрабатывать навыки нахождения скорости сближения, скорости удаления, зависимости между величинами: скорость, время, расстояние. Воспитательные: воспитывать уважение к предмету, умение видеть математические задачи в окружающем мире, воспитывать навыки дисциплинированных пешеходов, соблюдающих правила дорожного движения. Развивающие: развивать умение находить способы решения задач и выделять рациональные способы решения; развивать пространственное воображение и образное мышление; развивать умения применять знания на практике. Оборудование: учебник Л.Г.Петерсон «Математика» 4 класс, часть 2, наглядный материал, иллюстрирующий различные виды движения, круги двух цветов (зелёный, красный) для рефлексии, карточки с задачами. Ход урока: 1. Организационный момент. Самоопределение к деятельности. - Запишите в тетради: Число. Классная работа. - Поработаем устно. Это задание поможет нам сформулировать тему урока. - Найдите значение выражений и расшифруйте запись, которая станет эпиграфом урока. 70·10 – 3 ·90 = 430 360:4:18·5 = 25 42 – 320:80·4 = 26 2 6/8 + 3 4/8 – 2 7/8 = 3 3/8 7 5/9 – (2 4/9 +1/9) = 5 без жить с могут 165 5 25 192 Люди 430 12 6/10 – 4 5/10 + 1 9/10 = 10 движения. 106 4·30 + 9·8 = 192 рождения 3 3/8 не самого 10 26 150 – 640 : 80 + 23 = 165 201·6 – 1100 = 106 Люди с самого рождения жить не могут без движения. - Итак, сегодня на уроке мы будем повторять и обобщать знания о различных видах движения, будем решать задачи на движение. - Запишите в тетради: Задачи. 2. Актуализация знаний. (На доске наглядный материал, иллюстрирующий улицу, пешеходов, автомобили, различные виды движения.) - Вот наша улица. По её проезжей части мчатся автомобили, проходят троллейбусы и автобусы. На тротуарах пешеходы. Всё в движении. Рассмотрите, какие случаи движения представлены на доске? (Встречное движение, движение в противоположных направлениях, движение вдогонку, движение с отставанием.) - Что происходит с расстоянием во время встречного движения и движения вдогонку? (Расстояние уменьшается.) - Что происходит в конце концов с объектами? (Они встречаются.) - О какой скорости в этих случаях мы говорим? (О скорости сближения.) - Что называется скоростью сближения? (Расстояние, на которое сближаются объекты за единицу времени, называется скоростью сближения.) - Как находим скорость сближения в случае встречного движения? (Vсбл.= V1 + V2) (На доску постепенно вывешиваются таблицы с различными видами движения.) - А в случае движения вдогонку? (Vсбл.= V1 - V2) - Что происходит с расстоянием во время движения в противоположных направлениях и движения с отставанием? (Расстояние увеличивается.) - Происходит ли встреча в данных случаях? (Нет.) - О какой скорости мы говорим здесь? (О скорости удаления.) - Что называется скоростью удаления? (Расстояние, на которое удаляются объекты за единицу времени, называется скоростью удаления.) - Как находим скорость удаления в случае движения в противоположных направлениях? (Vуд. .= V1 + V2) - Как находим скорость удаления в случае движения с отставанием? (Vуд. .= V1 - V2) - Используя данные с доски, составьте задачи, в которых надо найти скорость сближения или скорость удаления. (Устное решение составленных детьми задач.) – А теперь решите мою задачу: Из двух домов одновременно выбежали девочка и мальчик и бегут в школу. Девочка бежит со скоростью 80 м/мин и мальчик со скоростью 80 м/мин. Им надо перейти через дорогу. Кто быстрее попадёт в школу? Почему? (Ответы детей.) - Для того, чтобы на улицах было безопасно, надо соблюдать правила дорожного движения. Такие правила должны знать и водители, и пешеходы. Что означают эти знаки? («Осторожно - дети!», «Пешеходный переход».) - Первый предупреждает водителей, что рядом находится школа или какое-либо другое учебное заведение. А второй указывает, что в данном месте пешеходный переход, и только здесь можно перейти проезжую часть. - Где ещё можно переходить улицу? (Там, где есть светофор.) 3. Локализация затруднений. - На протяжении нескольких уроков мы учились решать задачи про различные движущиеся объекты: про самолёты, машины, поезда. А сегодня я хочу предложить вам задачи про вас. Посмотрим, сможете ли вы вычислить свою скорость при движении, расстояние или время, которое вам потребуется? - Попробуем решить задачу про кого-то из вас. Серёжа начал догонять Алину, когда расстояние между ними было 120 м. Серёжа идет со скоростью 60 м/мин, а Алина – со скоростью, составляющей 2/3 от скорости Серёжи. Через сколько минут Серёжа догонит Алину? 4. Построение проекта выхода из затруднений. - Как вы думаете, с чего начнём? - Какую формулу надо вспомнить? - Надо ли обратить внимание на вид движения? Вспомнить формулу одновременного движения. Определить вид движения. Выбрать нужную формулу для решения задачи. - Вспомните формулу одновременного движения. Как найти первоначальное расстояние между объектами? (Первоначальное расстояние равно скорости сближения, умноженной на время до встречи s = v сбл. · tвстр.) (На доску вывешивается формула одновременного движения.) - Для каких видов движения подходит эта формула? (Для встречного и движения вдогонку.) - Одинаково ли будем находить первоначальное расстояние в случае встречного движения и в случае движения вдогонку? (Разница лишь в том, что при встречном движении Vсбл.= V1 + V2 , а при движении вдогонку Vсбл.= V1 - V2.) - Почему эта формула не подходит для движения в противоположных направлениях и движения с отставанием? (В этих случаях расстояние между объектами увеличивается и встреча не произойдёт.) - Но ведь расстояние между объектами можно найти в любой момент времени. Что для этого надо сделать? (Скорость сближения или удаления умножить на время.) (На доску вывешивается формула s = v уд. · t .) - И полученное число прибавить, если идёт увеличение расстояния, или вычесть, если идёт его уменьшение, из первоначального расстояния. - Эти формулы напоминают обычную формулу пути. (На доску вывешивается формула s = v · t .) - Только значения s, v, t (расстояние, скорость, время) наполнены особым смыслом. 5.Обобщение затруднений во внешней речи. - Какой вид движения представлен в задаче? (Движение вдогонку.) - Какие объекты движутся? (Серёжа и Алина.) - С какой скорость идёт Серёжа? (60 м/мин) - А Алина? (Её скорость составляет 2/3 от скорости Серёжи.) - Что надо узнать в задаче? (Через сколько минут Серёжа догонит Алину, т.е. время до встречи.) - Как узнать время до встречи? (Надо первоначальное расстояние разделить на скорость сближения.) - Можем сразу ответить на главный вопрос? (Нет.) - Почему? (Мы не знаем скорость Алины и скорость сближения.) - Можем узнать скорость Алины? Как? (Да. 60:3·2) - Узнав скорость Алины, сможем узнать скорость сближения? (Да.) - Каким действием? (Вычитанием.) - Затем сможем узнать, через сколько минут Серёжа догонит Алину, т.е. время до встречи? (Да.) - Каким действием? (Делением.) - Запишите решение задачи, ответ. 1) 60:3·2=40 (м/мин) – скорость Алины. 2) 60 – 40 = 20 (м/мин) – скорость сближения. 2) 120: 20 =6 (мин)- время до встречи. Ответ: Серёжа догонит Алину через 6 минут. - Решим ещё одну задачу. Никита и Саша договорились покататься на велосипедах. Они выехали навстречу друг другу одновременно из своих домов, расстояние между которыми 2 км 225 м. Никита ехал со скоростью 240 м/мин, и через 5 минут мальчики встретились. С какой скоростью ехал Саша? - Нам известно расстояние и время? Что можем найти? (Скорость сближения.) - Как? (Чтобы найти скорость сближения, надо первоначальное расстояние разделить на время.) - Узнав скорость сближения, сможем найти скорость Саши? Как? (Да. Из скорости сближения вычесть скорость Никиты.) 1) 2 225 : 5 = 445(м/мин) – скорость сближения. 2) 445 – 240 = 205(м/мин) – скорость Саши Ответ: скорость Саши 205 м/мин. 6. Самостоятельная работа с самопроверкой по эталону. - А следующие задачи решите самостоятельно. (Дети работают самостоятельно.) Задача №1. Маша и Лиза вышли одновременно из школы и пошли домой в противоположных направлениях. Скорость Лизы 50 м/мин, а скорость Маши на 10 м/мин меньше. На каком расстоянии они буду находиться друг от друга через 15 минут? 1) 50-10=40 (м/мин) – скорость Маши. 2) 50+40=90 (м/мин) – скорость удаления. 3) 90 ·15=1350 (м) – расстояние. Ответ: расстояние через 15 минут 1км 350 м. Задача №2. На уроке физкультуры Вова бежал со скоростью 100 м/мин, Ваня догонял его со скоростью 85 м/мин. Как изменяется расстояние между ними за 1 минуту? Какое расстояние будет между ними через 5 минут? 1) 100-85=15 (м/мин) – скорость удаления. 2) 15·5=75 (м) – расстояние через 5 минут. Ответ: Вова за 1 минуту удаляется на 15 м, расстояние через 5 минут 75 метров. Задача №3. Папа Кирилла поехал в Москву. Расстояние между Липецком и Москвой 450 км. Сколько времени потребуется папе на проезд туда и обратно, если он будет ехать со скоростью 90 км/ч, в Москве задержится на 5 часов, а в пути сделает две остановки по 30 минут? 1) (450+450):90=10 (ч) – время в пути. 2) 30 ·2=60 (мин) – время остановок. 3) 10+5+1=16 (ч) – всего. Ответ: папе потребуется 16 часов. - Проверьте решение задач по эталону на доске. Физкультминутка Люди с самого рождения жить не могут без движения Руки опустите вниз, держите спину ровно, голову не наклоняйте. Медленно поднимайте руки вверх и сцепите их в замок над головой. Представьте, что ваше тело – как гора. Одна половина горы говорит: «Сила во мне» и тянется вверх. Другая говорит: «Нет, сила во мне» и тоже тянется вверх. «Нет!» - решили они – две половинки одной горы – сила в нас обеих». Потянулись обе вместе, сильно-сильно. Медленно опустите руки и улыбнитесь. 7. Включение в систему знаний и повторения. - И ещё одна задача. Расстояние от дома Миши до школы равно 500 м. Миша проходит этот путь за 20 минут. Однажды он прошёл половину пути и вспомнил, что забыл дома дневник. Ему пришлось вернуться. На сколько он должен увеличить свою скорость, чтобы вернуться домой за дневником и успеть в школу к началу урока? - Мы знаем расстояние от дома Миши до школы и время, которое он тратит на дорогу. Что можем узнать? (Скорость Миши.) - Каким действием? (Делением.) - Какое выражение запишем? 1) 500:2=25 (м/мин) – скорость Миши. - Он прошёл половину пути. Как узнать, сколько он прошёл? 2) 500:2=250 (м) – половина пути. - Как узнать, сколько времени он потратил? 3) 20:2=10 (мин) – половина времени. - Ему пришлось вернуться, то есть его путь увеличился. На сколько? Сколько теперь ему надо пройти? 4) 500+250=750 (м) – надо пройти Мише. - А времени сколько у него осталось? (10 минут.) - Узнаем, с какой скоростью ему надо преодолеть 750 м за 10 минут. 5) 750:10=75 (м/мин) – новая скорость Миши. - Скорость Миши была 25 м/мин, а должна стать 75 м/мин. На сколько же надо её увеличить? 6) 75-25=50 (м/мин) – на столько увеличить. Ответ: надо увеличить скорость на 50 м/мин. 8. Рефлексия учебной деятельности (итог урока) - Ну что же, Миша взял дневник, увеличил свою скорость, улицу перешёл в положенном месте и успел к началу урока. А вы знаете, почему Мише так необходим дневник? Чтобы получить в него очередную пятёрку. Я думаю, что он её сегодня получает. А ещё получают … - А теперь я попрошу вас самих оценить себя и свою деятельность на уроке. У вас на столах «сигналы» - круги двух цветов светофора для пешеходов: зелёного и красного. Если вам на уроке было интересно, если вы отвечали правильно на все вопросы, если у вас всё получилось, прикрепите к доске ЗЕЛЁНЫЙ сигнал. Если у вас возникали затруднения в ходе работы, но вы с ними справились, прикрепите КРАСНЫЙ сигнал. (Дети прикрепляют к доске «сигналы».) - Зелёный сигнал светофора показывает, что движение открыто. Что ж, будем двигаться дальше, к новым знаниям. - Всем спасибо. Урок окончен.