работа №4. Энтропия источника дискретных Лабораторная

Лабораторная работа
сообщений без памяти
№4.
Энтропия
источника
дискретных
В лабораторной работе исследуется энтропия источника дискретных
сообщений без памяти и двоичного кодирующего устройства на основе кода
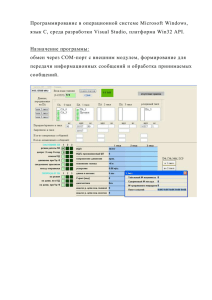
Windows 1251. Схема исследуемого устройства приведена на рис. 4.1.
Источник
сообщения
{ai }
Windows1251
{bi }
Двоичный {bi}
{ai}
симетричный
Windows1251
канал связи
Получатель
сообщения
Ошибка
Рис. 4.1. Схема лабораторной работы
Мера информации содержащийся в сообщении {ai } оценивается как:
k
H ( A)    P(ai ) log( P(ai )) .
i 1
1
Максимальное значение H ( A) будет принимать если P(ai )  , i  1..k , в
k
этом случае
k 1
1
H ( A)  H ( A) max    log( )  log( k )
(2.11)
k
k
i 1
Для источника дискретных сообщений вводится понятие избыточности
источника:
H ( A)
,
(2.12)
pи  1 
H ( A) max
pи является безразмерной величиной в пределах [0..1].
Для определения предельных характеристик дискретных каналов связи
К.Шенноном была введена была введена величина названная пропускной
способностью канала связи C
C  к max( H ( B)  H ( B / B))  к max( H ( B)  H ( B / B)) . (2.24)
0  C  к log( m)
При полностью независимых входе и выходе канала связи (канал связи
полностью забит помехами) C  0 . Максимальное значение C   к log( m) ,
получается если в канале связи нет помех H ( B / B )  0 и
H ( B)  H ( B) max  log( m) .
Например, в случае двоичного дискретного канала связи ( m  2 ), при
заданной вероятности ошибки в канале p , пропускная способность будет
равна
C  k (log( 2)  (1  p) log( 1  p)  p log( p)) .
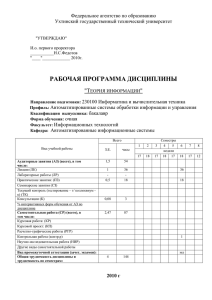
График нормированной
представлен на рис. 4.2.
пропускной
способности
канала
связи
Из рис. 4.2 видно что пропускная
способность
канала
связи
максимальная в случае если
ошибок в канале связи нет p  0 ,
или в случае если p  1 , то есть
каждый передаваемый символ
меняется на противоположное
значение (фактически канал
связи работает в качестве
Рис. 4.2. График зависимости
p  0,5 –
инвертора). Если
нормированной пропускной
вероятность приема символа не
способности двоичного дискретного
канала связи от вероятности ошибки в зависит от того какой символ
канале связи
передает источник сообщения и в
этом
случае
пропускная
способность канала связи C  0 .
Выполнение лабораторной работы
Этап I
Исследовать работу дискретного канала связи в программе лабораторной
работы TIPSlab4.exe. Для этого ввести сообщение преобразовать его в
двоичный код. Проанализировать значение ансамбля сообщений источника
сообщений и кодера (приемника и декодера).
Проанализировать влияние вероятности ошибки дискретного канала связи
на значения ансамбля получаемого при приеме сообщения.
Составить график нормированной пропускной способности дискретного
канала связи.
Внешний вид окна программы лабораторной работы представлен на
рис. 4.3. Окно вывода статистики источника (приемника) дискретных
сообщений показано на рис. 4.4.
Рис. 4.3. Внешний вид программы лабораторной работы
Рис. 4.4. Окно вывода статистики источника дискретных сообщений
Этап II
Составить программу вычисления энтропии, максимальной энтропии и
избыточности источника дискретных сообщений по введенным данным.
Для ввода строки в MatLab, рекомендуется использовать функцию input()
с ключом ‘s’:
S=input(‘введите строку’,’s’) ;
Добавление к строке значения 0 позволяет получить массив со значениями
кодов символов строки. Размерность массива вычисляется с помощью
функции size().
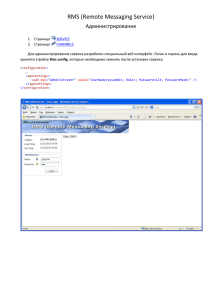
В программе представленной на блок–схеме рис. 4.5, в массиве Р
вычисляется вероятность появления символа. Номер элемента массива
соответствует при этом коду символа. При вычислении меры информации,
содержащийся в каждом символе на блок–семе показан обход ситуации при
которой Pi  0 , приводящий к аварийному завершению программы (попытка
вычисления log( 0) ).
P=P/L
Hmax = log2(K)
H=0; K=0
Pi = 1- H / Hmax
i= 1
H, Hmax, Pi
S
S= S+ 0
P = zero(256)
L = size(S )
i < 256
i= 1
P[i] > 0
H=H+P(i)*log2(P (i))
i <= L
K=K+1
P(S (i)) = P(S(i))+ 1
i= i+ 1
i= i+ 1
Рис. 4.5. Блок–схема алгоритма вычисления информационных характеристик источника
дискретных сообщений без памяти
Содержание отчета
Отчет по лабораторной работе должен содержать:
1.
Пример сообщения и расчет энтропии, избыточности для
дискретного источника сообщений.
2.
Графики нормированной пропускной способности канала связи от
вероятности ошибки в канале связи.
3.
Алгоритм, листинг программы и тестовый пример расчета
информационных характеристик дискретного источника сообщений
без памяти в математическом пакете MatLab.
4.
Выводы по сравнению результатов, полученных на своей программе
и в программе лабораторной работы.