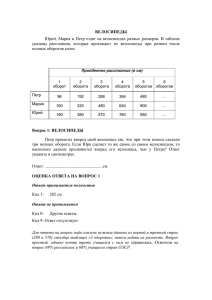
1.23. Зависимость углового ускорения колеса, вращающегося

1.23. Зависимость углового ускорения колеса, вращающегося
относительно неподвижной оси, перпендикулярной к его плоскости и
проходящей через его центр, от времени задана уравнением: ε=2+3t2 (с2).
Радиус колеса 0,3 м, масса 20 кг равномерно распределена по ободу.
Определить: угловой путь, пройденный за время от t1=1 с до t2=3 с;
полное число оборотов, сделанных колесом за это время; линейную скорость
точек на ободе колеса; момент импульса колеса в момент времени 3 с (при
t=0 ω=0).
Дано:
  2  3t 2 с2
R=0,3 м
m=20 кг
t1=1 с
t2=3 с
t0=0
ω0=0
Найти:
φ=?
N=?
v=?
L=?
Решение.
Угловое ускорение колеса:
d
,

dt
откуда
d =dt  (2  3t 2 )dt ,

t
 d =  (2  3t
0
2
)dt
0
  0 =2t  t 3 .
С учетом того, что ω0=0, получим закон изменения
угловой скорости:
d
=2t  t 3 с-1,
dt
d =(2t  t 3 )dt .
Принимая, что в начальный момент φ0=0, получим:
=

t
 d =  (2t  t )dt ,
3
0
0
t4
=t  , рад.
4
Из выражения для угловой скорости колеса следует, что при t>0 ее
направление не изменяется, т.е. угол поворота только увеличивается. Угловой
путь, пройденный за время от t1 с до t2, равен разности углов поворота в эти
моменты:
t24 2 t14
2
  (t2 )  (t1 )=t2   t1 
4
4
4
4
3
1
81
1
  32   12   9   1   8  20  28( рад)
4
4
4
4
Число оборотов за это время:

28
N

 4,46
2 2  3,14
Линейная скорость точек на ободе колеса связана с угловой скоростью
соотношением:
v  R=(2t  t 3 ) R .
2
Для момента времени t2 находим:
v(t2 )  (2t2  t23 ) R  (2  3  33 ) c 1  0,3 м  9,9
Момент импульса тела:
м
.
с
L  I ,
где I – момент инерции (для колеса относительно заданной оси вращения
I  mR 2 ).
L  mR 2 (2t  t 3 )
Для заданного момента времени
кг  м2
2
3
2 2
3
1
.
L  mR (2t2  t2 )  20 кг  0,3 м  (2  3  3 ) с  59,4
с
Ответ: угловой путь, пройденный колесом, φ=28 рад, число оборотов N=4,46,
линейная скорость точек на ободе колеса v=9,9 м/с, момент импульса колеса
L=59,4 кг·м2/с.
1.31. Платформа в виде диска вращается по инерции вокруг вертикальной
оси с частотой n1=15 оборотов в минуту. На краю платформы стоит человек.
Когда человек перешел в центр платформы, частота вращения возросла до 25
оборотов в минуту. Масса человека m=70 кг. Определить массу платформы М.
Человека считать точечной массой.
Дано:
n1=15 мин-1
n2=25 мин-1
m=70 кг
Найти:
М=?
Решение.
Момент инерции платформы:
MR 2
I
.
2
Момент инерции человека, стоящего на краю платформы,
относительно оси вращения:
Iч1  mR 2 .
После перехода в центр платформы его момент инерции Iч2=0.
Момент инерции системы в начальном состоянии:
MR 2
2m  M 2
I1  I  I ч1 
 mR 2 
R
2
2
Начальный момент импульса системы:
2m  M 2
L1  I11 
R  2n1  n1 (2m  M ) R 2 ,
2
1  2n1 - начальная угловая скорость вращения платформы.
Момент импульса системы после перехода человека в центр:
MR 2
I 2  I  Iч2 
,
2
поскольку момент инерции человека при этом равен нулю.
Момент импульса системы после перехода человека в центр:
MR 2
L2  I 22 
 2n2  n2 MR 2 .
2
Считая систему замкнутой, запишем закон сохранения момента
импульса:
L1  L2 ,
n1 (2m  M ) R 2  n2 MR 2
(2m  M )n1  Mn2 ,
2mn1  Mn2  Mn1  M (n2  n1 ) ,
2mn1
.
M
n2  n1
кг  мин1
 кг
M  
мин1
2  70 кг  15 мин 1
M
 210(кг )
(25  15) мин1
Ответ: масса платформы М=210 кг.
1.38. Двум одинаковым маховикам, выполненным в виде однородных
дисков радиусом 0,4 м и массой 1000 кг, сообщили одинаковую частоту
вращения 480 оборотов/мин. Под действием сил трения первый маховик
остановился через 1 мин 20 с, а второй маховик сделал до полной остановки
240 оборотов. Определить моменты сил трения, действовавшие на каждый из
маховиков, считая их величины постоянными во время вращения.
Дано:
Решение.
R=0,4 м
Момент инерции каждого из маховиков:
m=1000 кг
mR 2
-1
I

I

I

.
1
2
n0=480 об/мин=8 c
2
t1=1 мин 20 с=80 c
Применим к первому маховику теорему об
N2=240
изменении момента импульса:
Найти:
dL
 Me.
Mтр1=?
dt
Mтр2=?
В качестве момента внешних сил выступает момент силы трения Мтр1.
Считая его постоянным, получим:
L1
t1
 dL   M
L01
0
t1
dt  M тр1  dt
тр1
0
L1  L01  M тр1t1 .
В момент остановки L1=0, тогда
L01
I 0
2n0mR 2
n0mR 2
,
M тр1  



t1
t1
2t1
t1
где ω0=2πn0 – начальная угловая скорость вращения маховика. Знак "-"
указывает, что момент тормозит движение тела.
3,14  8 с 1  1000 кг  0,42 м2
M тр1  
 50,2 Н  м .
80 с
Ко второму маховику применим теорему об изменении кинетической
энергии:
T  A ,
где T  T  T0 - изменение кинетической энергии системы,
А – работа всех сил.
В конце движения Т=0 (тело останавливается). Поскольку маховик
совершает вращательное движение, его начальная кинетическая энергия
I 02 mR 2  (2n0 ) 2
T0 

 2 n02 mR 2 .
2
4
Работа постоянного момента сил сопротивления при повороте на угол φ:
A  M тр 2  M тр 2  2N 2  2N 2 M тр 2 ,
поскольку при каждом обороте угол увеличивается на 2π рад.
Отсюда
2n02mR2  2N2 M тр 2 ,
n02mR 2
.
M тр 2  
2 N2
3,14  82 с 2  1000 кг  0,42 м2
 67,0 Н  м .
2  240
Ответ: моменты сил трения, действовавшие на маховики Мтр1=-50,2 Н·м,
Мтр2=-67,0 Н·м.
M тр 2  
2.6. Бесконечная равномерно заряженная нить и шар расположены, как
показано на рис. Заряд шара 10-9 Кл; линейная плотность заряда на нити
5·10-10 Кл/см; а=10 см. Окружающая
среда – воздух.
Определить:
напряженность поля в точках А и В; работу перемещения заряда 10 -8 Кл из
точки А в точку В. Считать, что расположение зарядов не нарушено
взаимодействием.
Дано:
Q=10-9 Кл
=5·10-10 Кл/см=5·10-8 Кл/м
а=10 см=0,1 м
ε=1
q=10-8 Кл


2
Найти:
ЕА=?
ЕВ=?
А=?
Решение.
Согласно принципу суперпозиции полей, напряженность поля в точке А
EA  EA1  EA2 ,
где EA1 , EA2 – напряженности полей, созданных в точке А нитью и шаром
соответственно.
Модуль напряженности поля бесконечной равномерно заряженной нити:

,
E1 
20 r1
где r1 – расстояние от оси нити.
Вектор напряженности нити направлен перпендикулярно нити (при >0 –
от нее). При r1=а получим:

E A1 
.
20 a
Напряженность поля шара на расстоянии r2≥R (радиуса шара) от его
центра
Q
E2 
,
40 r22
вектор направлен радиально (при Q>0 – от центра шара).
Для точки А при r2=а
Q
.
E A2 
40 a 2

Учитывая, что угол между векторами E A1 и E A 2 равен   , по теореме
2
Пифагора находим результирующую напряженность в точке А:
2
2
    Q 
1
Q2
2
EA  E  E  

  2 .
 
2 
2

a
4

a
2

a
4a
0 
0
0



Для точки В получаем;
EB  EB1  EB 2 ,
где напряженности полей получим из тех же формул при r1=2а, r2=а:

,
EB1 
40 a
Q
.
EB 2 
40 a 2
2
A1
2
A2
Учитывая, что векторы EB1 , EB 2 направлены одинаково, получим:

Q
1 
Q
EB  EB1  EB 2 





.
40 a 40 a 2 40 a 
a
Потенциал поля бесконечной равномерно заряженной нити:
r1


r
1    E1dr   
dr 
ln 0 ,
20 r
20 r1
r0
где r0 – радиус цилиндра (нити), потенциал поверхности нити принят равным
нулю.
Для потенциала поля шара имеем:
Q
2 
 0 ,
40 r2
где φ0 – константа, зависящая от выбора точки с нулевым потенциалом.
С учетом принципа суперпозиции находим потенциалы точек А и В:

r
Q
 A   A1   A2 
ln 0 
 0 ,
20 a 40 a

r
Q
B  B1  B 2 
ln 0 
 0 .
20 2a 40 a
Работа поля по перемещению заряда q из точки А в точку В:
 

r
Q

r
Q
A  q ( A   B )  q 
ln 0 
 0 
ln 0 
 0  
20 2a 40 a
 20 a 40 a


 r 2a 
q  r0
r0 
q
q
ln  0   
ln 2 .
 ln  ln  
20  a
2a 
20  a r0  20
1
Кл 2 Кл 2
В Кл В
[ EA ] 





2
2
Ф
м
м
Кл
м
м
м
м
1  Кл Кл  В Кл В
[ EВ ] 





Ф
м
м
Кл
м
м


м
м
[ A] 
Кл
м  Кл 2  В  Кл  В  Дж
Ф
Кл
м
Кл 
1
1018
2
16
EA 
5  10 
 9  103 ( В / м)  9(кВ / м)
12
2
2  1  8,85  10  0,1
4  0,1

1
109 
8
3
EB 
 5  10 
  5,4  10 ( В / м)  5,4( кВ / м)
12
4  1  8,85  10  0,1 
0,1 
108  5  108
A
 ln 2  6,2  106 ( Дж )  6,2( мкДж )
12
2  3,14  1  8,85  10
Ответ: напряженность поля в точке А ЕА=9 кВ/м, в точке В ЕВ=5,4 кВ/м, работа
поля по перемещению заряда q из точки А в точку В А=6,2 мкДж.
2.11. Потенциал электростатического поля задан выражением
10
,
( x, y, z ) 
( x  a ) 2  ( y  b) 2  ( z  c ) 2
где а=b=с=0,1 м.
Определить напряженность электростатического поля в точке
координатами х=0,2 м, у=-0,2 м, z=0,1 м.
Дано:
Решение.
Связь напряженности поля с
потенциалом:
E   grad  ,



E i 
j k,
x
y
y
где i , j , k - орты декартовой системы
координат.
10
( x, y, z ) 
( x  a ) 2  ( y  b) 2  ( z  c ) 2
а=b=с=0,1 м
х=0,2 м
у=-0,2 м
z=0,1 м
Найти:
Е=?
Проекции вектора E на оси координат:


1
Ex  

10(( x  a)2  ( y  b) 2  ( z  c) 2 ) 2 
x
x
1
10( x  a)
3
 10   (( x  a)2  ( y  b)2  ( z  c)2 ) 2  2( x  a) 
3 ,
2
(( x  a)2  ( y  b)2  ( z  c)2 ) 2







10( y  b)
1
10(( x  a)2  ( y  b)2  ( z  c)2 ) 2 
3 ,
y
(( x  a)2  ( y  b)2  ( z  c)2 ) 2

10( z  c)
1
Ez  
10(( x  a)2  ( y  b)2  ( z  c)2 ) 2 
3 .
z
(( x  a)2  ( y  b)2  ( z  c)2 ) 2
Для заданной точки
10  (0,2  0,1)
Ex ( x, y, z ) 
3  31,6( В / м) ,
2
2
2 2
((0,2  0,1)  (0,2  0,1)  (0,1  0,1) )
10  (0,2  0,1)
E y ( x, y, z ) 
3  95( В / м)
((0,2  0,1)2  (0,2  0,1) 2  (0,1  0,1) 2 ) 2
10  (0,1  0,1)
Ez ( x, y, z ) 
3  0
((0,2  0,1)2  (0,2  0,1) 2  (0,1  0,1) 2 ) 2
E  31,6i  95 j .
Модуль вектора напряженности
Ey  
с
E  Ex2  E y2  Ez2  32,62  (95)2  02  100( В / м)
Ответ: модуль вектора напряженности поля в заданной точке равен 100 В/м.
2.23. Сферический конденсатор состоит из двух концентрических
обкладок радиусами 10 см и 14 см, пространство между которыми заполнено
диэлектриком с диэлектрической проницаемостью равной 6. Конденсатор
заряжен до напряжения 100 В.
Определить энергию, заключенную между сферическими поверхностями
радиусами 11 см и 13 см.
Дано:
R1=10 см=0,1 м
R2=14 см=0,14 м
ε=6
U=100 В
r1=11 см=0,11 м
r2=13 см=0,13 м
Найти:
W=?
Решение.
Объемная плотность энергии электрического поля:
D2
.
w
20
Найдем модуль электрического смещения в пространстве между
обкладками. Из сферической симметрии системы следует, что вектор смещения
направлен вдоль радиуса, а его модуль зависит только от расстояния от центра
сфер. Выберем поверхность S в виде сферы радиуса R1<r<R2, концентрической
с обкладками. Применим теорему Остроградского-Гаусса для вектора
смещения:
 DdS   DndS  Q ,
S
S
где Q – суммарный свободный заряд, находящийся внутри поверхности.
Внутри выбранной поверхности находится заряд сферической обкладки
радиуса R1, равный заряду конденсатора. Тогда, учитывая, что для всех точек
выбранной поверхности модуль вектора D одинаков и направлен вдоль
нормали к поверхности, т.е. Dn  D  const , получим:
 D dS  D  dS  Q ,
n
S
S
D  4r  Q ,
Q
.
D
4r 2
Объемная плотность энергии электрического поля:
2
1  Q 
Q2
w

 
20  4r 2  3220 r 4
Энергия электрического поля внутри объема
W   wdV .
2
V
Исходя из симметрии системы, выберем элемент объема в виде
сферического слоя, ограниченного сферами радиусов r и r+dr, тогда
dV  4r 2dr ,
r
r2
r
Q2
Q 2 2 dr
Q2 1 2
Q 2  1 1  Q 2 (r2  r1 )
2
W 
 4r dr 



.
  
2
4
2

32


r
8

r
8

r
8

r
r
8

r
r
r1
0
0 r1
0
0  1
2 
0 1 2
r1
Заряд конденсатора
где C  40
Q  CU ,
R1R2
- емкость сферического конденсатора.
R2  R2
40UR1R2
,
Q
R2  R2
2
(r  r )  40UR1R2  20 (r2  r1 ) R12 R22 2
W 2 1 
U .
 
80 r1r2  R2  R1 
r1r2 ( R2  R1 ) 2
Ф
 м  м2  м2
Кл 2
[W ]  м 2 2
 В2 
 В  Кл  В  Дж
м м
В
2  6  8,85  1012  (0,13  0,11)  0,12  0,142
W
 1002  5,7  107 ( Дж )  0,57( мкДж )
2
0,11  0,13  (0,14  0,1)
Ответ: энергия электрического поля внутри выбранного объема W=0,57 мкДж.
Задача №2.36.
В
некоторого проводника
количество
тепла
длиной 2 м за 2 с выделяется
.
Определить:
напряжение
на
концах
проводника; скорость упорядоченного движения и подвижность электронов в
проводнике, считая концентрацию электронов
Дано:
Найти:
.
Решение:
Количество тепла, которое выделяется в проводнике вычисляется по формуле:
,
где
–
сопротивление
проводника,
который
равен
. Отсюда
Отсюда выразим напряжение:
Подставим числовые значения:
Заряд, протекающий по проводнику равен
где
–
количество
электронов,
, силу тока равна
, отсюда
которое
найдем
, отсюда
по
формуле
.
Приравняем правые части уравнений (1) и (2) и выразим отсюда скорость:
Подставим числовые значения:
Подвижностью
называют
коэффициент
пропорциональности
между скоростью носителей тока и величиной приложенного электрического
поля
Ответ:
, т.е.
напряжение
на
концах
проводника
равно
126,5
В;
скорость
упорядоченного движения равна 39,5 мкм/с, а подвижность электронов в
проводнике равна
.