Задача “Песочница”

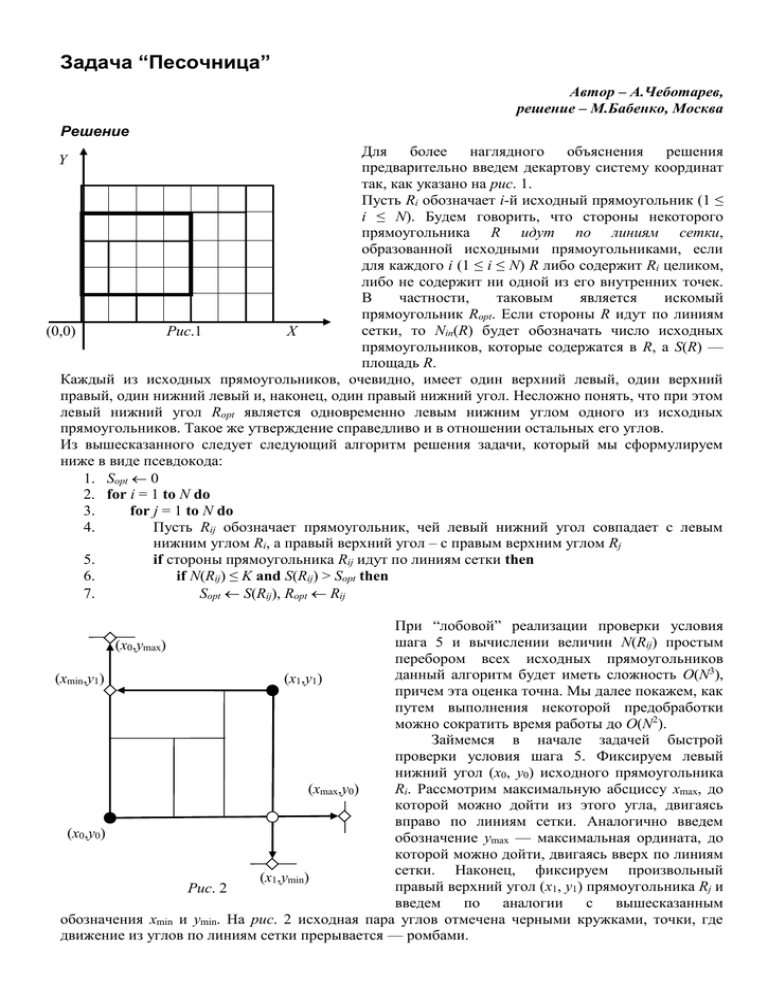
Задача “Песочница”
Автор – А.Чеботарев,
решение – М.Бабенко, Москва
Решение
Для более наглядного объяснения решения
предварительно введем декартову систему координат
так, как указано на рис. 1.
Пусть Ri обозначает i-й исходный прямоугольник (1 ≤
i ≤ N). Будем говорить, что стороны некоторого
прямоугольника R идут по линиям сетки,
образованной исходными прямоугольниками, если
для каждого i (1 ≤ i ≤ N) R либо содержит Ri целиком,
либо не содержит ни одной из его внутренних точек.
В
частности,
таковым
является
искомый
прямоугольник Ropt. Если стороны R идут по линиям
сетки, то Nin(R) будет обозначать число исходных
(0,0)
Рис.1
X
прямоугольников, которые содержатся в R, а S(R) —
площадь R.
Каждый из исходных прямоугольников, очевидно, имеет один верхний левый, один верхний
правый, один нижний левый и, наконец, один правый нижний угол. Несложно понять, что при этом
левый нижний угол Ropt является одновременно левым нижним углом одного из исходных
прямоугольников. Такое же утверждение справедливо и в отношении остальных его углов.
Из вышесказанного следует следующий алгоритм решения задачи, который мы сформулируем
ниже в виде псевдокода:
1. Sopt  0
2. for i = 1 to N do
3.
for j = 1 to N do
4.
Пусть Rij обозначает прямоугольник, чей левый нижний угол совпадает с левым
нижним углом Ri, а правый верхний угол – с правым верхним углом Rj
5.
if стороны прямоугольника Rij идут по линиям сетки then
6.
if N(Rij) ≤ K and S(Rij) > Sopt then
7.
Sopt  S(Rij), Ropt  Rij
Y
При “лобовой” реализации проверки условия
шага 5 и вычислении величин N(Rij) простым
(x0,ymax)
перебором всех исходных прямоугольников
данный алгоритм будет иметь сложность O(N3),
(xmin,y1)
(x1,y1)
причем эта оценка точна. Мы далее покажем, как
путем выполнения некоторой предобработки
можно сократить время работы до O(N2).
Займемся в начале задачей быстрой
проверки условия шага 5. Фиксируем левый
нижний угол (x0, y0) исходного прямоугольника
(xmax,y0)
Ri. Рассмотрим максимальную абсциссу xmax, до
которой можно дойти из этого угла, двигаясь
вправо по линиям сетки. Аналогично введем
(x0,y0)
обозначение ymax — максимальная ордината, до
которой можно дойти, двигаясь вверх по линиям
сетки. Наконец, фиксируем произвольный
(x1,ymin)
правый верхний угол (x1, y1) прямоугольника Rj и
Рис. 2
введем по аналогии с вышесказанным
обозначения xmin и ymin. На рис. 2 исходная пара углов отмечена черными кружками, точки, где
движение из углов по линиям сетки прерывается — ромбами.
Из рисунка также следует, что прямоугольник Rij идет по линям сетки, если и только если
выполняются следующие неравенства: xmax ≥ x1, ymax ≥ y1, xmin ≤ x0, ymin ≤ y0. Предвычисление
величин xmax, ymax (для каждого левого нижнего угла) и xmin, ymin (для каждого правого верхнего
угла) легко провести за общее квадратичное время. Действительно всего углов O(N), а вычисление
для каждого из них сводится к просмотру списка прямоугольников и нахождению ближайшей
“преграды”.
Теперь проверка условия шага 5 может быть выполнена за время O(1), однако общая
сложность алгоритма по-прежнему останется кубической, поскольку вычисление N(Rij) на шаге 6
занимает линейное время. К счастью, подходящая предобработка может помочь и в этом случае.
Для угла A = (x0, y0) каждого из прямоугольников Ri пусть W(A) обозначает число таких j, что Rj
целиком лежит в квадранте плоскости, определяемом неравенствами x ≥ x0, y ≥ y0. Очевидно, все 4N
чисел W() можно вычислить за время O(N2).
Пусть рассматривается прямоугольник Rij.
Введем обозначения: A — левый нижний угол Ri, D —
правый верхний угол Rj. Если A = (x0, y0), D = (x1, y1),
то должны существовать узлы сетки B = (x1, y0) и C =
W(D)
W(C)–W(D)
(x0, y1), причем эти точки должны быть
соответственно правым нижним и левым верхним
углами некоторых исходных прямоугольников.
C
D
Остается только заметить, что справедливо
соотношение: N(Rij) = W(A) – W(B) – W(C) + W(D). Его
W(A)–W(B)–
W(B)–W(D)
доказательство оставляется читателю в качестве
W(C)+W(D)
упражнения и сводится к рассмотрению возможных
положений прямоугольников относительно точек A и
D. Рис. 3 поясняет вышесказанное.
B
A
Несмотря на всю простоту алгоритма, тем не
Рис. 3
менее, остается одна существенная проблема. Даже
вычислив предварительно значения W(), для
применения этой комбинаторной формулы помимо точек A и D требуется знание еще и точек B и
C. Конечно, их координаты просто получить из координат A и D, но при фактической реализации
массив W будет индексироваться номерами углов прямоугольников, а не их координатами.
Возможны два способа решения данной проблемы. Первый из них состоит в предварительном
составлении списка всех углов исходных прямоугольников и его лексикографической сортировке.
Данная операция потребует O(NlogN) времени (заметим, что здесь можно применить даже
квадратичный алгоритм). После этого для получения номера угла по его координатам достаточно
осуществить бинарный поиск в отсортированном массиве. Такой подход позволит вычислить
любое из значений N(Rij) за время O(logN), а следовательно общая сложность всего алгоритма
будет O(N2logN).
Иной способ использует то свойство, что возможных значений координат углов
прямоугольников довольно мало. Их число не превосходит N + 1 по каждому измерению.
Обозначим все возможные значения X1, …, Xs и Y1, …, Yt соответственно, при этом считаем, что
каждая их этих последовательностей идет в возрастающем порядке. Тем самым установлено
взаимнооднозначное соответствие между возможными координатами и начальным отрезком
натурального ряда. Пусть на шаге 2 алгоритма была фиксирована вершина A, тогда поскольку YB =
YA и XC = XA, то достаточно построить два массива
 xlist[q] будет обозначать номер прямоугольника, чей правый нижний угол имеет координаты
(Xq, YA) или 0, если таких прямоугольников нет;
 ylist[q] будет обозначать номер прямоугольника, чей левый верхний угол имеет координаты
(XA, Yq) или 0, если таких прямоугольников нет.
При наличии этих массивов определение номеров прямоугольников для углов B и С тривиально
выполняется за время O(1). Построение массивов требует времени O(N) на каждой итерации цикла
2, а потому общие расходы на их построение будут O(N2), что не превышает сложности остальных
частей алгоритма. Поскольку эти массивы используются только в пределах одной итерации (при
фиксированном значении i), то объем дополнительной памяти для алгоритма линеен.