Зачет по теме: «Перпендикулярность в прос транстве»
реклама

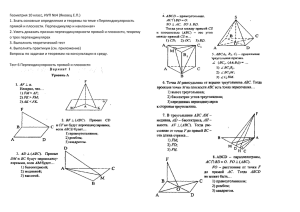
Зачет по теме: «Перпендикулярность в пространстве» 1.Дайте определение перпендикулярности прямой и плоскости. 2.Теорема о трех перпендикулярах. 3.Какие плоскости называются перпендикулярными? 4.Точка О – центр квадрата со стороной а; ОА – отрезок, перпендикулярный к плоскости квадрата и равный b. Найдите расстояние от точки А до вершин квадрата. 5.Стороны треугольника равны 13 см, 14 см, 15 см. Точка М расположенная вне плоскости треугольника, удалена от всех сторон треугольника на 5 см. Определите расстояние от точки М до плоскости треугольника. 6.Через вершину С ромба АВСД проведена прямая МС, перпендикулярная сторонам ромба ВС и СД. О – точка пересечения диагоналей ромба. Докажите перпендикулярность прямой ВД и плоскости МОС и найдите площадь ромба, если МВ = 10см, МО = 8 см, ВД : АС = 2:3. Зачет по теме: «Перпендикулярность в пространстве» 1.Признак перпендикулярности прямой и плоскости. 2.Что называется расстоянием от точки до плоскости? 3. Свойства перпендикулярных прямых и плоскости. 4.Диагонали квадрата АВСД пересекаются в точке О. Из точки О проведен к плоскости квадрата перпендикуляр ОМ. Найдите расстояние от точки М до вершин квадрата, если АД = 6 см, ОМ = 4 см. 5.Стороны треугольника равны 13 см, 14 см, 15 см. Точка М расположенная вне плоскости треугольника, удаленная от всех сторон треугольника, находится на расстоянии 3 см от плоскости треугольника. Определите расстояние от точки М до сторон треугольника. 6. Через вершину В прямоугольника АВСД проведена прямая МВ, перпендикулярная сторонам прямоугольника АВ и ВС. Докажите перпендикулярность прямой СД и плоскости МВС и найдите площадь прямоугольника, если МД = 13см, МС = 12 см, АД : СД = 8:5. Зачет по теме: «Перпендикулярность в пространстве» Зачет по теме: «Перпендикулярность в пространстве» 1.Признак перпендикулярности плоскостей. 1.Определение перпендикулярности прямой и плоскости. 2.Теорема о трех перпендикулярах. 2.Что называется расстоянием от точки до плоскости? 3.Какие прямые называются перпендикулярными? 3. Свойства перпендикулярных прямых и плоскости. 4.Точка О – центр квадрата со стороной а; ОА – отрезок, перпендикулярный к плоскости квадрата и равный b. Найдите расстояние от точки А до вершин квадрата. 4.Диагонали квадрата АВСД пересекаются в точке О. Из точки О проведен к плоскости квадрата перпендикуляр ОМ. Найдите расстояние от точки М до вершин квадрата, если АД = 6 см, ОМ = 4 см. 5.Стороны треугольника равны 13 см, 14 см, 15 см. Точка М расположенная вне плоскости треугольника, удалена от всех сторон треугольника на 5 см. Определите расстояние от точки М до плоскости треугольника. 5.Стороны треугольника равны 13 см, 14 см, 15 см. Точка М расположенная вне плоскости треугольника, удаленная от всех сторон треугольника, находится на расстоянии 3 см от плоскости треугольника. Определите расстояние от точки М до сторон треугольника. 6.Через вершину С ромба АВСД проведена прямая МС, перпендикулярная сторонам ромба ВС и СД. О – точка перечения диагоналей ромба. Докажите перпендикулярность пря- 6. Через вершину В прямоугольника АВСД проведена прямая мой ВД и плоскости МОС и найдите площадь ромба, если МВ, перпендикулярная сторонам прямоугольника АВ и ВС. МВ = 10см, МО = 8 см, ВД : АС = 2:3. Докажите перпендикулярность прямой СД и плоскости МВС и найдите площадь прямоугольника, если МД = 13см, МС = 12 см, АД : СД = 8:5. Зачет по теме: «Перпендикулярность в пространстве» Зачет по теме: «Перпендикулярность в пространстве» 1.Что называется расстоянием от точки до плоскости? 2. Свойства перпендикулярных прямых и плоскости. 3.Признак перпендикулярности прямой и плоскости. 1.Признак перпендикулярности плоскостей. 2.Теорема о трех перпендикулярах. 3.Дайте определение перпендикулярности прямой и плоскости. 4.Из вершины равностороннего треугольника АВС восстановлен перпендикуляр АД к плоскости треугольника. Чему равно расстояние от точки Д до прямой ВС, если АД = 1 дм, ВС = 8 дм? 4.Из вершины квадрата АВСД восстановлен перпендикуляр АЕ к плоскости квадрата. Чему равно расстояние от точки Е до прямой ВД, если АЕ = 2 дм, АВ = 8 дм? 5.Гипопотенуза прямоугольного треугольника равна 12 см. Вне плоскости треугольника дана точка, удаленная от всех вершин треугольника на расстояние 10 см. Найдите расстояние от этой точки до плоскости треугольника. 5. В равнобедренном треугольнике основание и высота равны по 8 см. Точка А удалена от плоскости треугольника на 12 см и равноудалена от его вершин. Найдите расстояние от точки А до вершин треугольника. 6. Стороны треугольника равны 10 см, 17 см, 21 см. Из вершины большего угла проведен перпендикуляр к плоскости треугольника, равный 15 см. Определите расстояние от его концов до большей стороны. 6.Диагонали ромба АВСД равны 30 см и 40 см. Из вершины А ромба проведен к плоскости перпендикуляр АК. Найдите расстояние от точки К до противоположной стороны ромба, если АК = 10 см. 7. Через сторону АД ромба АВСД проведена плоскость . Найдите расстояние от прямой ВС до плоскости , если площадь ромба равна 20 см2, сторона – 5 см, а угол между проекциями стороны СД и высоты СН (Н АД) равен 45 0 . 7. Катет и гипотенуза прямоугольного треугольника соответственно равны 12 и 15 см. Расстояния от данной точки до сторон треугольника равны 5 см. Найдите расстояние от данной точки до плоскости треугольника.