Модели ИИСС «Уравнения и неравенства»
реклама
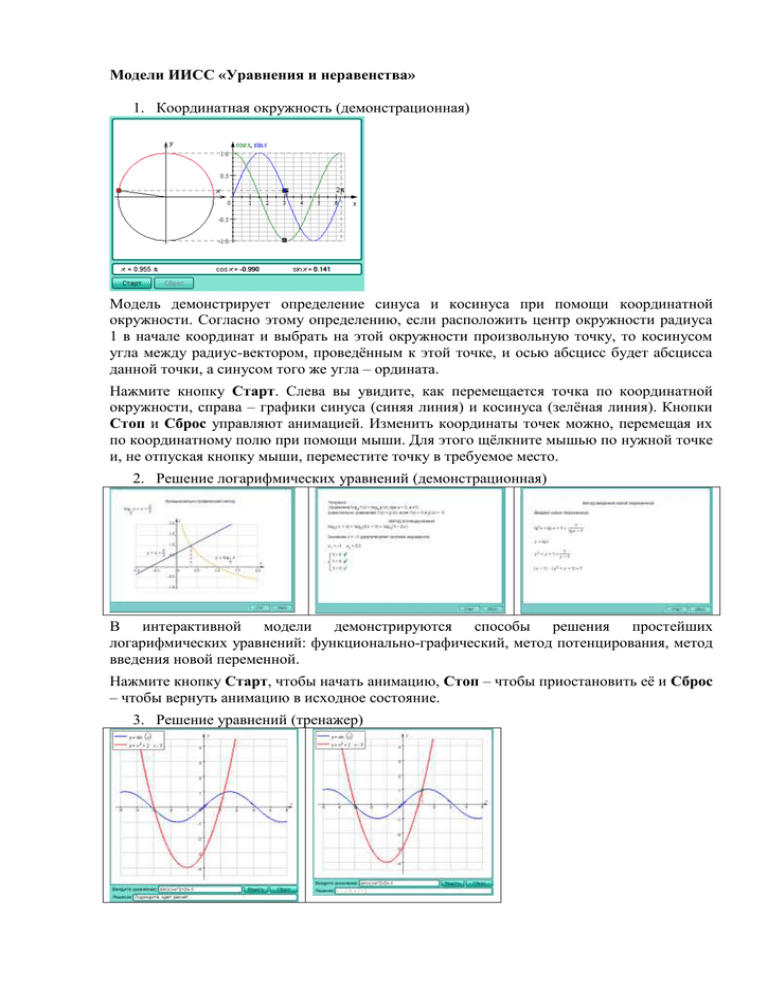
Модели ИИСС «Уравнения и неравенства» 1. Координатная окружность (демонстрационная) Модель демонстрирует определение синуса и косинуса при помощи координатной окружности. Согласно этому определению, если расположить центр окружности радиуса 1 в начале координат и выбрать на этой окружности произвольную точку, то косинусом угла между радиус-вектором, проведённым к этой точке, и осью абсцисс будет абсцисса данной точки, а синусом того же угла – ордината. Нажмите кнопку Старт. Слева вы увидите, как перемещается точка по координатной окружности, справа – графики синуса (синяя линия) и косинуса (зелёная линия). Кнопки Стоп и Сброс управляют анимацией. Изменить координаты точек можно, перемещая их по координатному полю при помощи мыши. Для этого щёлкните мышью по нужной точке и, не отпуская кнопку мыши, переместите точку в требуемое место. 2. Решение логарифмических уравнений (демонстрационная) В интерактивной модели демонстрируются способы решения простейших логарифмических уравнений: функционально-графический, метод потенцирования, метод введения новой переменной. Нажмите кнопку Старт, чтобы начать анимацию, Стоп – чтобы приостановить её и Сброс – чтобы вернуть анимацию в исходное состояние. 3. Решение уравнений (тренажер) Введите в верхнее поле ввода уравнение в виде f (x) = g (x), например, sin x = x2 – 2x + 3. Нажмите кнопку Enter или Решить. Подождите некоторое время. Будет построен график правой и левой частей уравнения, зелёными точками будут отмечены корни, записаны корни уравнения. Чтобы ввести новое уравнение, нажмите кнопку Сброс. Если вы сделаете ошибку при вводе, в нижнем окне появится соответствующее сообщение. 4. Метод деления отрезка пополам (тренажер) Интерактивная модель демонстрирует один из наиболее распространенных способов нахождения нулей функции на отрезке (и решения алгебраических уравнений) – метод деления отрезка пополам. Введите функцию в поле ввода в правом верхнем углу модели. Задайте границы отрезка [a; b], на котором ищутся нули, при помощи полей численного ввода. Нажмите кнопку Сделать шаг. Программа определит, является функция на отрезке [a; b] монотонной и непрерывной. Если функция не является непрерывной, то в окне вывода будет выдано сообщение об этом; вам будет предложено уточнить границы отрезка, на котором ищутся нули. То же самое произойдет, если предполагаемых нулей функции на данном отрезке будет слишком много (примером является поиск нулей функции y = cos x на отрезке [–2; 2]). Продолжайте нажимать кнопку Сделать шаг. Следите на графике функции и в окне вывода за тем, как изменяются границы отрезков, на которых ищутся нули. Через несколько шагов нули будут найдены с точностью до сотых. Кнопка Сброс возвращает модель в исходное состояние. 5. Решение показательных уравнений Показательными уравнениями называют уравнения вида где a – положительное число, отличное от 0, и уравнения, сводящиеся к этому виду. В интерактивной модели демонстрируются способы решения простейших показательных уравнений. Нажмите кнопку Старт, чтобы начать анимацию, Стоп – чтобы приостановить её и Сброс – чтобы вернуть анимацию в исходное состояние. 6. Решение неравенств графическим методом Введите в верхнее поле ввода неравенство в виде f (x) ? g (x), где знаком «?» обозначена какая-либо из операций сравнения «<», «<=», «>», «>=», например, sin(x)>=2*exp(x). Нажмите кнопку Enter или Решить. Подождите некоторое время. Будет построен график правой и левой частей неравенства, штриховкой по оси абсцисс будет отмечено решение. В нижней части модели выводятся приблизительные решения с точностью до 0,1. Чтобы ввести новое неравенство, нажмите кнопку Сброс. Если вы сделаете ошибку при вводе, в нижнем окне появится соответствующее сообщение. 7. Метод интервалов Интерактивная модель демонстрирует один из методов решения дробно-рациональных неравенств – метод интервалов. Общий вид левой части неравенства записан в левой части модели. В правой части неравенства находится 0. Между этими частями могут стоять знаки «>», «<», «=», «≥», «≤»; выбор нужного знака осуществляется при помощи соответствующего переключателя. Задайте параметры C, ai, bi, αi, βi (для 1 ≤ i ≤ 3). Графическая иллюстрация к методу интервалов появится в верхней части модели. Точки, входящие в решение неравенства, будут выделены зелёным цветом. Формульную запись решения можно увидеть в окне вывода в нижней части модели. 8. Колебания в электрической цепи. Колебания в электрической цепи происходят по закону синуса или косинуса. Так, в цепи изображенной в правом верхнем углу модели, заряд на обладках конденсатора изменяется по закону q = CU + (q0 – CU) cos ωt, где C – емкость конденсатора, U – напряжение на источнике тока, L – индуктивность катушки, – угловая частота колебаний в цепи. Установите параметры колебательного контура и нажмите Старт. В левой части модели начнут строиться графики q (t) и I (t). Текущие значения t, q и I появятся в нижней части окна вывода. Кнопка Стоп приостанавливает анимацию, кнопка Сброс возвращает модель в исходное состояние. 9. Функция синус Интерактивная модель демонстрирует график тригонометрической функции y = A sin (ax + b) + B. Введите значения коэффициентов функции в численные поля ввода и нажмите кнопку Построить. На экране появится синусоида. Можно задать координату некоторой точки из области определения функции (в единицах π). На экране появится значение функции в этой точке. 10. Функция косинус Интерактивная модель демонстрирует график тригонометрической функции y = A cos (ax + b) + B. Введите значения коэффициентов функции в численные поля ввода и нажмите кнопку Построить. На экране появится косинусоида. Можно задать координату некоторой точки из области определения функции (в единицах π). На экране появится значение функции в этой точке. 11. Простейшие тригонометрические уравнения Модель позволяет в интерактивном режиме решать простейшие тригонометрические уравнения. Введите в верхнее поле ввода уравнение вида A f (ax + b) = B (например, 2*tg(3*x+4)=0.5) и нажмите кнопку Решить. Через некоторое время в среднем поле появится ответ. В качестве функции f можно вводить sin, cos, tg и ctg. Если вы допустили ошибку при вводе, то в нижнем поле появится сообщение об ошибке. Чтобы очистить поле ввода, нажмите Сброс. 12. Решение тригонометрических неравенств Тригонометрическими неравенствами называются неравенства, в которые входят тригонометрические функции и их композиции. Решениями тригонометрических неравенств являются, как правило, серии интервалов, отстоящих друг от друга на некоторое число. В интерактивном режиме выбирается, какая тригонометрическая функция входит в неравенство, и задаются коэффициенты. Программа автоматически находит решение неравенства и рисует его графически. Чтобы перейти в демонстрационный режим, щёлкните по кнопке с кинопроектором. Нажмите кнопку Старт, чтобы начать анимацию, Стоп – чтобы приостановить её и Сброс – чтобы вернуть анимацию в исходное состояние. Для возвращения в интерактивный режим нажмите на кнопку с изображением руки. 13. Тригонометр Модель демонстрирует определение основных тригонометрических функций при помощи координатной окружности. Также, модель позволяет в интерактивном режиме решать простейшие тригонометрические уравнения и неравенства. Для демонстрации значений основных тригонометрических функций выберите режим «Значения основных тригонометрических функций». С помощью выпадающего списка выберите необходимую тригонометрическую функцию. Угол можно задавать тремя способами: 1. Вбивать значение угла в поле для ввода. 2. Изменять значение угла в поле для ввода с помощью. 3. Изменить координату точки, перемещая их по координатному полю при помощи мыши. В режиме «Решение тригонометрических уравнений/неравенств» можно выбирать основные тригонометрические функции для решения простейших уравнений и неравенств, а также вид уравнения/неравенства. Предусмотрено решение уравнений/неравенств для табличных значений тригонометрических функций. 14. Графер (виртуальный практикум) Программа «Графер» предназначена для построения и преобразования графиков функций различного вида. Она обеспечивает демонстрацию связи формулы и графика функций. Для школьников использование модели облегчает изучение графиков функций, обеспечивает наглядность и простоту в использовании. Для преподавателей модель может служить хорошим средством для подготовки к занятиям, для создания наглядных пособий и так далее. Построение графиков функций можно производить в декартовой и полярной системах координат. Пользователь может самостоятельно задать функцию вида y = f (x), параметрического вида y = f (t), x = g (t) или полярную функцию r = r (t). Имеется набор «стандартных» функций: степенных, тригонометрических и гиперболических. К графикам функций можно строить касательные. Модель даёт возможность производить над функциями и их графиками различные преобразования: смещение графика функций относительно координатных осей, сжатие, растяжение, зеркальное отображение относительно осей координат. Можно производить взаимные преобразования нескольких функций, такие как сложение функций, умножение и деление одной функции на другую, преобразование вида f (g (x)). При этом соответствующие преобразования одновременно влияют как на графическое изображение функции, так и на её аналитический вид. Имеются различного рода графические возможности, предназначенные для оформления графиков функций, для придания им более наглядного вида. Можно ставить надписи, отмечать точки, отрезки, интервалы и многое другое. Так как для построения функций используются численные, а не аналитические методы, возможны некоторые неточности построения в сложных критических точках. Инструкция для ученика. Введение Пользовательский интерфейс Практическая работа Как построить график функции Как изменить параметры графика функции Построение элементарных графиков функций Как изменить масштаб координатной плоскости Как удалить, сохранить данные, извлечь сохранённые данные Преобразования графиков и их функций Как добавить вспомогательную информацию Схематические надписи и рисунки Формулы Кнопки «На задний план» и «На передний план» Дополнительные графические возможности Графера