Лабораторная работа №1 Исследование однофазного трансформатора 1.2.1.1.1
реклама

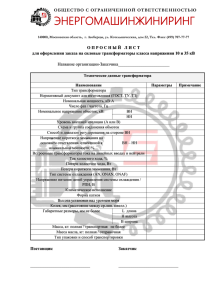
Лабораторная работа №1 1.2.1.1.1 Исследование однофазного трансформатора 1.Цель работы: исследование однофазного трансформатора при работе с активной нагрузкой. 2.Указания к выполнению работы. К выполнению работы следует приступить после изучения разделов, посвященных работе однофазного трансформатора, настоящего пособия. В качестве дополнительной литературы рекомендуется воспользоваться [Бруск]. 3.Содержание работы. 3.1.Определение параметров трансформаторов различной мощности с помощью двух опытов: холостого хода и короткого замыкания. 3.2.Снятие нагрузочных и рабочих характеристик трансформатора. 3.3.Построение векторных диаграмм и определение падения напряжения на трансформаторе с помощью векторной диаграммы, а также аналитическим способом с помощью выражения (1-13) (настоящее пособие). 3.4. Сравнение результатов расчета по этим способам. 1.2.1.1.1.1.1 Описание виртуальной лабораторной установки. Схема установки изображена на рис. Л1-1. Виртуальная модель содержит: E1 - источник переменной ЭДС (библиотека Power System Blocset / Electrical Sources); V1 ,V2 - измерители напряжения в первичной и вторичной цепях трансформатора (библиотека Power System Blockset / Measurement); i1 , i2 - измерители тока первичной и вторичной обмоток трансформатора (библиотека Power System Blockset / Measurement); P, Q - измеритель активной мощности в первичной цепи однофазного трансформатора (библиотека Power System Blockset / Extras / Measurement); Powergui – блок пользователя, в который записываются результаты измерений блоков V1 ,V2 , i1 , i2 ; Display- блок количественного представления измеренных мощностей (библиотека Simulink / Sinks); Scope- блок наблюдения кривых тока и напряжения во вторичной цепи (библиотека Simulink /Sinks Рис. Л1-1. Модель для исследования однофазного трансформатора. Окно настройки параметров однофазного трансформатора показано на рис. Л1-2. Рис. Л1-2. Окно настройки параметров трансформатора. В полях окна настройки задаются: - Pn , f n - полная мощность трансформатора и номинальная частота (ВА и Гц); - V1 , R1 , L1 - действующее напряжение, активное сопротивление и индуктивность рассеяния первичной обмотки трансформатора - V2 , R2 , L2 - действующее напряжение, активное сопротивление и индуктивность рассеяния вторичной обмотки трансформатора; - Lm , Rm - индуктивность ветви намагничивания и сопротивление потерь в ферромагнитном сердечнике; - Heasurments- переменные состояния трансформатора, которые измеряются блоком Multimeter. Основная схема замещения трансформатора представлена на рис. Л1-3. Она учитывает активные сопротивления обмоток ( R1 , R2 , R3 ) , индуктивности рассеяния ( L1 , L2 , L3 ) , а также магнитные параметры сердечника, который представлен в виде ветви Rm , Lm с линейными характеристиками. Параметры схемы замещения трансформатора представлены в относительных единицах. Базовыми значениями параметров трансформатора являются: расчетная мощность в ВА, номинальная частота в Гц, действующее номинальное напряжение в В соответствующей обмотки. Для каждой обмотки относительные сопротивления и индуктивность определяются выражениями: R p.u. R LH R V ; L p.u. ; Rbase n ; Lbase base 2 f n Rbase Lbase Pn 2 (1-17) Для магнитных сопротивлений: резистивного Rm и индуктивного Lm относительные единицы базируются на расчетной мощности трансформатора и номинальном напряжении его обмотки. Для примера, параметры (“по умолчанию”) первичной обмотки дают следующие базовые значения: (735e3 / sqrt (3)) 2 720,3 Rbase 720,3Ом; Lbase 1.91Гн . 6 250e 2 60 Полагая, что параметрами первичной обмотки являются: R1 1, 44Ом и L1 0,1528Гн , соответствующими значениями, фиксированными в диалоговом окне, являются: 1, 44(Ом) 0,1528( Гн) R1 0, 002 p.u.; L1 0, 008 p.u. 720,3(Ом) 1,91( Гн) Чтобы точно установить (специфицировать) ток намагничивания, равный (в относительных единицах) 0,2% (активная и реактивная составляющие) по отношению к номинальному току, необходимо ввести относительные величины (p.u.) 1 / 0,002=500 p.u. для резистивного и индуктивного сопротивлений ветви намагничивания. При этом соответствующие величины Rm и Lm будут равны: Rm 3, 6e5Ом и Lm 995Ом . Относительные величины параметров первичной и вторичной обмоток равны между собой, также равны между собой и относительные величины параметров ветви намагничивания. (В приложении приведены данные силовых трансформаторов.) В окне настройки (рис. Л1-2) внесены относительные параметры трансформатора ТС-100 / 066. Если в лабораторной работе исследуется двухобмоточный трансформатор, то в поле параметров для третьей обмотки вводится нуль. Поскольку блок Multimeter не используется, то в поле Measurement из выпадающего меню выбрана опция None. Окно настройки параметров источника питания показано на рис. Л1-4. Рис. Л1-4. Окно настройки параметров источников питания. В полях окна задаются: - амплитуда источника питания (В); - начальная фаза в градусах; - частота в Гц; - образец времени (с); -переменные, измеряемые блоком Multimeter (если он не используется, то в соответствующем окне ставится нуль). Напряжение и частота источника должны соответствовать параметрам трансформатора. Окно настройки параметров нагрузки показано на рис. Л1-5. Рис. Л1-5. Окно настройки параметров нагрузки. В полях окна задаются величины R,L,C - параметры нагрузки. Для исключения реактивных элементов индуктивность должна быть задана, равной нулю, а емкость бесконечности (inf). В окне настройки параметров измерителя активной и реактивной мощности (рис. Л1-6) указывается частота, на которой измеряется активная и реактивная мощности. Рис. Л1-6. Окно настройки измерителя активной и реактивной мощностей. Окно настройки параметров дисплея показано на рис. Л1-7. В его полях окон настройки указывается формат представления числовых результатов, в поле Decimation (разрежение) задается число шагов вычисления, через которые значения результатов выводятся на дисплей. Подробное описание блока Scope приведено в гл.1. Рис. Л1-7. Окно настройки параметров дисплея. Действующие (и амплитудные) значения напряжений и токов трансформатора при различных режимах его работы отображаются в окне блока Powergui (рис. Л1-8). Рис. Л1-8. Действующие значения напряжения и токов. Как было показано выше, точность определения параметров трансформатора зависит от относительной величиной тока холостого хода, которая в мощных трансформаторах составляет всего лишь несколько процентов от намагничивающего тока, а в трансформаторах малой мощности она может достигать 60%. В лабораторной работе необходимо определить параметры, как мощного трансформатора, так и маломощного с относительно большим током намагничивания. Для второго типа трансформатора его параметры следует определить двумя способами: 1)без учета потерь в первичной обмотке трансформатора в режиме холостого хода и потерь в ферромагнитном сердечнике в режиме короткого замыкания; 2)с учетом этих потерь и оценить погрешности экспериментального определения параметров трансформатора обеими способами. В режиме холостого хода определяется также коэффициент трансформации исследуемого трансформатора. 1.2.1.2 Определение параметров трансформатора большой мощности В качестве примера определим параметры трансформатора большой мощности типа ТС-100 / 066. Параметры модели рассматриваемого трансформатора представлены на рис. Л1-9. Рис. Л1-9. Параметры трансформатора большой мощности типа ТС 100/066. 1.Режим холостого хода. На рис. Л1-10 изображена схема виртуальной установки для измерения параметров, на рис. Л1-11- результаты измерения действующих значений напряжений и токов первичной и вторичной обмоток, а на рис. Л1-12- осциллограммы кривых напряжений первичной и вторичной обмоток и тока первичной обмотки трансформатора в режиме холостого хода. Рис. Л1-10. Модель и результаты моделирования трансформатора большой мощности типа ТС-100/066 в режиме холостого хода. Рис. Л1-11. Действующие напряжения и токи трансформатора большой мощности типа ТС-100/066 в режиме холостого хода. Рис. Л1-12. Осциллограммы кривых напряжения (V1), тока (I1) первичной обмотки и напряжения (V2) вторичной обмотки трансформатора большой мощности типа ТС-100/066 в режиме холостого хода. Показания приборов виртуальной установки в рассматриваемом режиме имеют вид: Pxx 499,89 Вт; I xx 1, 071A; U1 660 В; U 2 399,9 В. Вследствие высокого значения добротности первичной обмотки трансформатора (согласно выражению (1-1)) можно записать U E 660В , что позволяет найти величину Rm : U2 6602 871, 4Ом. Pxx 499,89 Найдем величину Rm , заложенную в модель. Для этого определим Rbase : Rm Rbase (U п )2 6602 4,356Ом ; Pn 105 Rm Rbase *200 4,356*200 871, 2Ом . Найдем ошибку в определении величины Rm : 871, 2 871, 4 *100% 0, 23%. 871, 2 Определим величину cos : P 499,89 cos xx 0, 707 . UI 660*1, 071 Следовательно, угол между активной и реактивной составляющими тока холостого хода трансформатора равен 450 , и активная составляющая комплексного сопротивления ветви намагничивания равна реактивной: xm Lm 2 fLm Rm , отсюда: Rm 871, 4 2, 774 Гн . 2 f 2 *50 Определим величину Lm математической модели: R 4,356 Lm Lbase * 200 base * 200 * 200 2, 773 Гн . 2 f 2 *50 Ошибка в определении Lm : 2, 773 2, 774 *100% 0, 04% . 2, 773 Коэффициент трансформации исследуемого трансформатора равен: U 660 Кт 1 1, 65. U 2 399,9 Lm 2. Режим короткого замыкания. На рис. Л1-13 изображена схема виртуальной установки, на рис. Л1-14- результаты измерения действующих значений напряжений и токов первичной и вторичной обмоток, на рис. Л1-15- осциллограммы напряжений и токов первичной и вторичной обмоток исследуемого трансформатора в режиме короткого замыкания. Рис. Л1-13. Модель и результаты моделирования мощного трансформатора типа ТС-100/066 в режиме короткого замыкания. Рис. Л1-14. Действующие напряжения и токи трансформатора большой мощности типа ТС-100/066 в режиме короткого замыкания. Рис. Л1-15. Осциллограммы кривых напряжения (V1) и тока (I1) первичной обмотки и кривая тока вторичной обмотки (I2) трансформатора большой мощности типа ТС -100/066 в режиме короткого замыкания. Подбираем такую величину входного напряжения, при которой по первичной обмотке “ закороченного“ трансформатора протекает номинальный ток. В результате имеем: U k 34, 26 В ; I k I n 147, 7 A; Pk 2850, 71Вт . Определяем R1 и R2 : P 2850, 71 R1 R2 k2 0, 0653Ом . 2 I n 2*147, 7 2 Величины R1 и R2 математической модели: R1 R2 Rbase * R1 p.u. 4,356*0, 015 0, 065Ом . Ошибка в определении R1 и R2 : 0, 0650 0, 0653 *100% 0,5% . 0, 0650 Определяем L1 и L2 . Модуль комплексного сопротивления трансформатора в режиме короткого замыкания: U k 34, 26 0, 232Ом . I n 147, 7 Индуктивное сопротивление короткого замыкания определится выражением: Zk xk Zk2 Rk2 . Учитывая, что Rk 2 R1 2 R2 , имеем xk ( L1 L2 ) 2 L1 2 L2 Zk2 4R12 0, 2322 0,13062 0,1917Ом . Отсюда имеем: 4 xk 0,1917 3, 052*10 Гн . 2* 2 f 2* 2 *50 Величины L1 и L2 математической модели: 4 4,536 L1 L2 Lp.u . Lbase 0, 022* 3, 051*10 Гн . 2 *50 Ошибка в определении L1 и L2 : 3, 051 3, 052 *100% 0, 03% . 3, 051 3. Режим нагрузки. На рис. Л1-16 изображена схема виртуальной установки. L1 L2 Рис. Л1-16. Модель мощного трансформатора типа ТС-100/066 в режиме нагрузки. Снимаем нагрузочную характеристику исследуемого трансформатора большой мощности типа ТС-100/066. Для этого: регулируем сопротивление нагрузки в пределах: ( 0,8 Rн ) и для каждого из сопротивлений нагрузки определяем величину выходного напряжения. Результаты эксперимента сводим в таблицу № Л1-1. Таблица 1.2.1.2.1.1.1 Rн Ом №Л1-1 16 12,8 6,4 3,2 1,6 1,28 U н В 399,9 398,7 398,4 396,9 393,9 387,9 384,9 I А 0 24,92 31,13 62,02 123,1 242,5 300,7 По данным этой таблицы на рис. Л1-17 построена нагрузочная характеристика исследуемого трансформатора большой мощности типа ТС-100/066. 402,00 400,00 398,00 U[В] 396,00 394,00 392,00 390,00 388,00 386,00 384,00 0,00 100,00 200,00 300,00 400,00 Iн[А] Рис. Л1-17. Нагрузочная характеристика мощного трансформатора типа ТС-100/066. Результаты измерений позволяют определить падение напряжения на трансформаторе: 660 U (400 387,9) K т (400 387,9) 19,97 В 400 или 19,97 U расч *100% 3, 02%. 660 Расчет падения напряжения на трансформаторе типа ТС-100/066 с использованием выражения (1-13) дает следующие результаты: I н Rk 147, 7 *0, 065* 2 0, 029; Uн 660 I x 147, 7 *0,1917 U kr н k 0, 043. Uн 660 U ka U % (U ka cos U kr sin ) 2 (U kr cos U ka sin ) 2 200 12 (0, 029 cos 00 0, 043sin 00 ) 2 1(0, 029 cos 00 0.043sin 00 ) 0.0291. 200 В процентах, по отношению к номинальному напряжению это составит: U %*100 0, 0291*100 2,91% . Величина ошибки при расчете падения напряжения на трансформаторе по формуле (113): 3, 02 2,91 *100% 3, 6%. 3, 02 3, 02 3, 4 100 12,5%. 3, 02 Определять величину падения напряжения на трансформаторе с помощью векторной диаграммы при такой малой величине падения напряжения (около 3%) нецелесообразно т.к. точность этого метода невысока. Коэффициент трансформации трансформатора типа ТС-100/066: E U 660 kт 1 1 1, 65. E2 E2 400 Коэффициент полезного действия исследуемого трансформатора для номинального режима работы: Pн 100000 *100 *100 96,8%. Pн Pхх Pк 100000 499,89 2850, 71 Используя модель исследуемого трансформатора, снимаем зависимость активной мощности от тока нагрузки. Результаты исследования заносятся в таблицу №Л1-2. P1 Вт 499,89 10466,1 12948,21 25301,66 49719,61 97374,37 120599,6 P2 Вт 0 9936,38 12401,79 24617,1 48492,3 94053,26 115759,23 I н А 0 24,92 31,13 62,02 123,1 242,5 300,7 % 0 94,9 95,7 97,3 97,5 96,6 95,9 По данным этой таблицы на рис. Л1-18 построена зависимость коэффициента полезного действия трансформатора большой мощности типа ТС-100/066 от тока нагрузки. 120,00 100,00 КПД[% ] 80,00 60,00 40,00 20,00 0,00 0,00 100,00 200,00 300,00 400,00 Iн[А] Рис. Л1-18. Зависимость коэффициента полезного действия трансформатора типа ТС-100/066 от тока нагрузки. Анализ полученных при исследовании трансформатора большой мощности результатов подтверждает известный в практике расчетов вывод: При исследовании холостого хода трансформатора величина активной мощности, выделяемой в активном сопротивлении первичной обмотки трансформатора пренебрежимо мала, также пренебрежимо мала и активная мощность, выделяемая в ферромагнитном сердечнике трансформатора в режиме “нормального” короткого замыкания. Определение параметров трансформатора малой мощности В качестве объекта исследования при расчете параметров маломощного трансформатора выбран трансформатор типа ТН36-127/220-50. Параметры модели рассматриваемого трансформатора представлены на рис. Л1-19. Рис. Л1-19. Параметры трансформатора малой мощности типа ТН36-127/220-50. 1.Режим холостого хода. На рис. Л1-20 показана схема виртуальной установки. Рис. Л1-20. Модель и результаты исследования трансформатора малой мощности типа ТН-36-127.220-50 в режиме холостого хода. На рис. Л1-21 представлены результаты измерения действующих значений напряжения и токов первичной и вторичной обмоток исследуемого трансформатора. Рис. Л1-21. Действующие напряжения и токи трансформатора малой мощности типа ТН-36-127/220-50 в режиме холостого хода. На рис. Л1-22 изображены осциллограммы напряжений и токов в этих обмотках. Рис, Л1-22. Осциллограммы кривых напряжения вторичной (V2), первичной (V1) обмоток и тока первичной обмотки (I1) трансформатора малой мощности типа ТН-36-127/220-50 в режиме холостого хода. Показания измерительных приборов в режиме холостого хода. I xx 0,1312 A ; Pxx 11,95Вт ; U1 127 В ; U 2 27, 49В ; I 2 0 A . Учитывая высокое значение добротности первичной обмотки трансформатора, можно считать U E =127В, что позволяет найти величину Rm : U 2 127 2 Rm 1349, 7Ом . Pxx 11,95 Найдем величину Rm , заложенную в математическую модель, предварительно определив Rbase и Lbase : (U п )2 127 2 R 448 Rbase 448Ом ; Lbase base 1, 426 Гн, Pn 36 2 f 2 *50 Rm Rbase *3 1344Ом . Ошибка в определении Rm : 1344 1349.7 100 0 0 0.42 0 0 . 1344 Определим величину cos : P 11.95 cos xx 0.717 . UI 127 *0.1312 Реактивная составляющая тока холостого хода трансформатора будет равна: I pxx I 1 cos2 0.1312* 1 0.7172 0.0914 A . Находим величину xm : xm U 127 1389.5Ом . I pxx 0.0914 Теперь можно найти Lm : x 1389.5 Lm m 4.423 Гн . 2 f 2 *50 Величина Lm математической модели определится из выражения: Lm Lbase *3 1, 426*3 4, 278 Гн. Ошибка в определении Lm : 4, 278 4, 423 *100 3,39% . 4, 278 2.Режим короткого замыкания. На рис. Л1-23 изображена схема виртуальной установки. Рис. Л1-23. Модель и результаты моделирования трансформатора малой мощности типа ТН-36-127/220-50 в режиме короткого замыкания. На рис. Л1-24 величины действующих напряжений и токов первичной и вторичной обмоток. 1.2.1.2.2 Рис. Л1-24. Действующие напряжения и токи трансформатора малой мощности типа ТН-36-127/ 220-50 в режиме короткого замыкания. На рис. Л1-25 изображены осциллограммы кривых напряжений и токов этих обмоток исследуемого маломощного трансформатора. Рис. Л1-25. Осциллограммы кривых напряжения (V1) и тока (I1) первичной обмотки и кривая тока вторичной обмотки (I2) трансформатора малой мощности типа ТН-36-127/220-50 в режиме короткого замыкания. Подбираем такую величину входного напряжения, при которой по первичной обмотке “закороченного” в “нормальном” режиме трансформатора протекает номинальный ток. В результате получаем: U k 12,75В ; I k I1н 0, 286 A ; Pk 3, 62Вт. Определяем R1 и R2 : R1 R2 Pk 3, 62 22,13Ом . 2 2 I н 2*0, 2862 Величины R1 и R2 математической модели: R1 R2 Rbase R1 p.u. 448*0, 05 22, 4Ом Ошибка в определении R1 и R2 : 22, 4 22.13 *100 1, 21% . 22, 4 Определяем L1 и L2 . Модуль комплексного сопротивления в режиме короткого замыкания Z k : Zk U k 12, 75 44, 6Ом. I н 0, 286 Индуктивная составляющая комплексного сопротивления xk короткого замыкания определится выражением: xk Zk2 Rk2 . 1.2.1.2.2.1 Учитывая зависимость Rk 2 R1 2 R2 , получаем xk ( L1 L2 ) 2 L1 2 L2 Zk2 4R12 44,62 4*22.132 5,5Ом. Отсюда находим индуктивные сопротивления L1 и L2 : xk 5,5 L1 L2 0, 00875 Гн . 2* 2 f 2* 2 *50 Величины L1 и L2 математической модели: R 448 L1 L2 Lp.u. Lbase 0, 005 base 0, 005* 0, 0071Гн . 2 f 2 *50 Ошибка в определении L1 и L2 : 0, 0071 0, 00875 0, 0071 0, 00875 100 100 23% . 0, 0071 0, 0071 1.2.1.2.2.2 Определяем КПД трансформатора Pн кос 100% . Pн Pxx Pk 1.2.1.2.2.3 Учитывая, что Pн 27,15Вт; Rн 28 23,33Ом; P1 41, 61Вт; Pxx 11,95Вт; Pk 3, 62 Вт, 1, 2 после подстановки, получаем: Pн 27,15 кос 100 100 63,55%. Pн Pxx Pk 27,15 11,95 3, 62 Действительная величина КПД определится из выражения: Pн 27,15 100 100 65, 23%. P1 41, 61 Как было показано выше, при исследовании маломощного трансформатора сам процесс исследования необходимо начинать с режима короткого замыкания, после чего, зная параметры первичной обмотки маломощного трансформатора, можно рассчитать и параметры его ветви намагничивания. Для повышения точности определения параметров маломощного трансформатора необходимо учитывать падении напряжения на первичной обмотке и активную мощность, выделяемую в ней, а также, при относительно больших токах холостого хода, и активную мощность, выделяемую в ферромагнитном сердечнике, в режиме короткого замыкания. (В данном случае, ввиду относительно небольшого тока холостого хода, активная мощность, выделяемая в ферромагнитном сердечнике трансформатора, в режиме короткого замыкания, не учитывалась). В рассматриваемом маломощном трансформаторе после проведения опыта короткого замыкания и определения параметров первичной и вторичной обмоток можно найти величину ЭДС первичной обмотки (с учетом падения напряжения на ней) в номинальном режиме работы маломощного трансформатора: 1 1 E K т (U 2 xx (U 2 хх U 2 н )) K т (U xx U 2 н ). 2 2 Здесь: 127 4,5 ; Kт коэффициент трансформации, равный 28 U 2 xx 27, 49В; U 2 н 25,17 В. После подстановки получаем: 1 1 E K т (U 2 xx U 2 н ) 4,5(27, 49 25,17) 118,5В. 2 2 Активная мощность, выделяемая в ферромагнитном сердечнике трансформатора в режиме холостого хода, определится из выражения: E 2 118.5 2 Pxx' ( ) * Pxx ( ) *11,95 11Вт. . U 2 xx kт 27.49 K т Активную мощность, выделяемую в первичной обмотке трансформатора, можно найти, воспользовавшись выражением: Pxx. м I xx2 * R1 0,1312* 22,13 0,38 Вт . Найдем величину КПД (с учетом рассмотренных потерь) с помощью выражения: Pн 27,15 ' 65.59%. ' Pн Pxx. м Pxx. м Pk 27,15 11 0.38 3, 62 Ошибка в определении величины КПД: 65,59 65, 23 0,36%. Таким образом, в рассматриваемом маломощном трансформаторе с током холостого хода, равном 1/3 от его номинального значения, использование обычной методики расчета КПД привело к ошибке в его определении, примерно, равной 2% (63,55% при точном значении 65,23%). Очевидно, что при относительно большей величине тока холостого хода величина ошибки в расчете будет значительно выше. Поэтому при определении параметров маломощных трансформаторов с относительно большими токами холостого хода целесообразно в режиме холостого хода учитывать потери в обмотке трансформатора, а в режиме короткого замыкания- потери в его ферромагнитном сердечнике. 3. Режим нагрузки. На рис. Л1-26 изображена схема виртуальной установки. Рис. Л1-26. Модель трансформатора малой мощности типа ТН-36-127/220-50 в режиме нагрузки. Снимаем нагрузочную характеристику исследуемого трансформатора малой мощности типа ТН-36-127/220-50. При этом сопротивление нагрузки изменяется в пределах: от Rн до Rн 0,8Rном и для каждого из сопротивлений нагрузки определяется величина выходного напряжения. Результаты эксперимента сводим в таблицу №Л1-3. Таблица 1.2.1.2.2.4 Rн Ом №Л1-3 230 100 93 80 69 62 57 U н В 27,5 27,2 26,9 26,9 26,8 26,7 26,6 26,5 26,4 26,4 25,9 25,6 0 0,12 0,22 0,29 0,34 0,39 0,43 0,47 0,49 0,53 0,71 0,9 I А 54 49,6 36 28,4 По данным таблицы на рисунке Л1-25 построена нагрузочная характеристика трансформатора. 28,00 27,50 U[В] 27,00 26,50 26,00 25,50 25,00 0,00 0,20 0,40 0,60 0,80 1,00 Iн[А] Рис. Л1-27. Нагрузочная характеристика маломощного трансформатора типа ТН-36-127/220-50. Падение напряжения на трансформаторе в режиме номинальной нагрузки равно: 127 U 27, 49 25,17 K m 27, 49 25,17 10, 72 В 27, 49 или 10, 72 U расч 100 8, 44 0 0 . 127 Используя выражение (1-13) для расчета падения напряжения на трансформаторе, получаем: U 0 0 U ka cos U kr sin 1 0.101 cos 0 0.012 sin 0 0 0 2 U kr cos U ka sin 200 2 12 0.012 cos 00 0.101sin 00 200 что с учетом номинального значения напряжения составляет: 2 0.101, U 0 0 100 0.101100 10.1 0 0 . Величина ошибки при расчете падения напряжения на трансформаторе по формуле (1-13): 10.72 10.1 100 0 0 5.8 0 0 . 10.72 Большая (примерно, в два раза) погрешность расчета падения напряжения на трансформаторе малой мощности (в номинальном режиме его работы) по сравнению с погрешностью в случае с трансформатором большой мощности вызвана пренебрежением активными мощностями, выделяемыми в первичной обмотке в режиме холостого хода и в ферромагнитном сердечнике в режиме короткого замыкания. На рис. Л1-26 изображена векторная диаграмма исследуемого трансформатора малой мощности. Она была построена на основании системы уравнений (1-9) и следующих данных: E 118,5B; K т 4,5; I 2' 0 I 2 1, 08 j 0,320 e 0, 24e j 0,32 A; K т 4,5 U L' 2 I 2' R2' 0, 24e j 0,32 * 22 5,3e j 0,3 B; 0 0 U L' 2 jI 2' xL' 2 j 0, 24e j 0,3 * 2, 75 0, 66e j 90,3 B; 0 0 I xx 0,13e j 45 A; I1 I xx I 2' ; 0 U R1 I1R1 I1 *22; U L1 jI1 xL1 jI1 *2,75. Из этой диаграммы находим величину падения напряжения на трансформаторе в режиме номинальной нагрузки: U в.д. 13В. В процентах по отношению к номинальному напряжению это составит: U в.д. 13 100 10, 2%. U ном 127 Величина ошибки определения падения напряжения на рассматриваемом маломощном трансформаторе при использовании векторной диаграммы: 8, 44 10, 2 100 20,9%. 8, 44 Точность расчета ошибки падения напряжения на трансформаторе с помощью векторной диаграммы значительно ниже, чем при использовании аналитического способа (выражение (1-13)). Используя модель исследуемого трансформатора малой мощности, определяем величины активных мощностей (выделяемых в нагрузке трансформатора, и потребляемых от источника питания) в зависимости от значений тока нагрузки. Результаты исследований заносятся в таблицу №Л1-4. Таблица №Л1-4 1.2.1.2.2.4.1 P1[ Вт] P2 [ Вт] I [ A] [%] 11,95 15,2 18,1 19,4 21,2 24,7 26,6 31,8 36,7 41,6 48,3 7,2 8,9 12,3 14 18,7 23 27,1 32,6 0,34 42,2 0,47 49,8 0,53 52,6 0,89 62,7 1,08 65,1 1,32 67,5 0 3,3 6,1 0 0 0,12 21,7 0,22 33,7 0,27 37,1 0,72 58,9 На рис. Л1-28 построен график зависимости КПД трансформатора малой мощности типа ТН-36-127/220-50 от тока нагрузки. 80,00 70,00 КПД[% ] 60,00 50,00 40,00 30,00 20,00 10,00 0,00 0,00 0,50 1,00 1,50 Iн[А] Рис. Л1-28. Зависимость коэффициента полезного действия трансформатора малой мощности типа ТН-36-127/220-50 от тока нагрузки. 1.2.1.2.2.4.1.1 1.2.1.2.2.4.1.2 1.2.1.2.2.4.1.2.1 Лабораторная работа №2 Исследование трехфазного трансформатора 1.Цель работы: исследование трехфазного трансформатора при различных группах соединения его обмоток. 2.Указания к выполнению работы. К выполнению лабораторной работы следует приступить после изучения разделов настоящего пособия, посвященных работе трехфазного трансформатора. В качестве дополнительной литературы рекомендуется воспользоваться [Брускин]. 3.Содержание работы. Определение характеристик трехфазного трансформатора при соединении его обмоток по схемам: “звезда-звезда”(Y/Y), ”звезда-треугольник”(Y/ ), “треугольник-треугольник”( / ) и “треугольник-звезда”( /Y). 4.Описание виртуальной лабораторной установки. Виртуальная лабораторная установка изображена на рис. Л2-1. Рис. Л2-1. Виртуальная модель трехфазного трансформатора. По сравнению с моделью однофазного трансформатора (см. лаб. раб. №1), здесь не используются блоки для измерения основных характеристик (основные характеристики трехфазного и однофазного трансформаторов идентичны), но добавлен блок Multimeter,измеряющий токи и напряжения трансформатора. Значения этих токов отчитываются с окна блока Powerqui. Окно настройки параметров трехфазного трансформатора показано на рис. Л2-2. Рис. Л2-2. Окно настройки трехфазного трансформатора. В отличие от окна настройки параметров однофазного трансформатора оно содержит два дополнительных поля: - Winding 1(ABC) connection – схема соединения первичных обмоток; - Winding 2(abc) connection – схема соединения вторичных обмоток. В выпадающем меню этих полей задается схема соединения. В поле Measurment выбрана опция “All measurment (VIFluxes)”, при которой измеряются напряжения и токи всех обмоток, а также токи намагничивания первичных обмоток. Окно блока Multimeter при этом выглядит так, как показано на рис. Л2-3. Рис. Л2-3. Окно блока Multimeter. В левом поле окна присутствуют все переменные состояния трансформатора; они выводятся в окно блока Powerqui после проведения каждого моделирования. В правое окно кнопкой Select перенесены те переменные, которые выбраны для наблюдения. Включенный флажок” Display signals at simulation stop” обеспечивает графический вывод выбранных переменных при моделировании. 1.2.1.3 Определение параметров трехфазного трансформатора большой мощности 1.2.1.4 В качестве примера определим параметры трехфазного трансформатора большой мощности с характеристиками, представленными на рис. Л2-4. Рис. Л2-4. Параметры трехфазного трансформатора большой мощности. 1. Режим холостого хода. На рис. Л2-5. изображена схема виртуальной установки для измерения параметров фазы А. Рис. Л2-5. Модель и результаты моделирования трехфазного трансформатора большой мощности в режиме холостого хода. На рис. Л2-6 приведены действующие значения напряжений и токов обмоток и тока контура намагничивания для схемы соединения Y / Y . Рис. Л2-6. Действующие значения напряжений и токов обмоток и тока контура намагничивания для схемы соединения Y / Y На рис. Л2-7 изображены осциллограммы кривых напряжений первичной и вторичной обмоток и тока контура намагничивания трехфазного трансформатора большой мощности в режиме холостого хода. Рис. Л2-7. Осциллограммы кривых первичной и вторичной обмоток и тока контура намагничивания трехфазного трансформатора большой мощности в режиме холостого хода. Модели для трансформаторов с соединениями: Y / , / и / Y ничем не отличаются от модели на рис. Л2-4, соответствующей группе соединений Y / Y . Аналогично производятся измерения вышеперечисленных параметров, и результаты сводятся в таблицу №Л2-1. Таблица№Л2-1 Y / Y Y / / / Y U1 660 U2 380 Pхх 199,94 I хх 0,429 660 658,2 199,94 0,429 1143 658,2 199,94 0,2474 1143 380 199,94 0,2474 Найдем активное сопротивление контура намагничивания Rm : ( Y / Y , Y / ): Rm U12 6602 2178, 7Ом; Pхх 199,94 11432 6534, 2Ом. 199,94 Определим значение Rm , заключенное в модели, для чего рассчитаем Rbase : ( / , / Y ): Rm ( Y / Y , Y / ): Rbase U n2 6602 4,36Ом; Pn 100000 ( / , / Y ): Rbase U n2 11432 13, 08Ом. Pn 100000 Теперь можно найти Rm : ( Y / Y , Y / ): Rm Rbase 500 4,36 500 2180Ом. ( / , / Y ): Rm Rbase 500 13,08 500 6540Ом. Ошибка в определении Rm : 2180 2178,8 100% 0, 06%; 2180 6540 6534, 2 100% 0, 09%. ( / , / Y ): 6540 ( Y / Y , Y / ): Определим cos : ( Y / Y , Y / ): cos Pхх 199,9 0, 707. UI 660 0, 429 Pхх 199,9 0, 707. UI 1143 0, 2474 Таким образом, угол между активной и реактивной составляющими тока холостого хода трехфазного трансформатора 450 и активная и реактивная составляющие комплексного сопротивления ветви намагничивания равны. ( / , / Y ): cos xm Lm 2 fLm Rm . Теперь найдем величину Lm : ( Y / Y , Y / ): xm 2178,7Ом; xm 2178, 7 6,93 Гн. 2 f 2 *50 ( / , / Y ): xm 6534, 2Ом; Lm Lm Величина Lm математической модели: xm 6534, 2 20,80 Гн. 2 f 2 *50 ( Y / Y , Y / ): Lm Lbase *500 ( / , / Y ): Lm Lbase *500 Rbase 4,36 *500 *500 6,94 Гн; Lbase 0, 014 Гн. 2 f 2*3,14*50 Rbase 13, 08 *500 *500 20,82 Гн; Lbase 0, 042 Гн. 2 f 2*3,14*50 Ошибка в определении Lm : 6,94 6,93 *100 0 0 0,14 0 0 . 6,94 20,82 20,80 ( / , / Y ): *100 0 0 0, 096 0 0 . 20,82 ( Y / Y , Y / ): Значения коэффициента трансформации трехфазного трансформатора К m U1 U2 для различных схем соединения приведен в таблице №Л2-2: Таблица №Л2-2 Кm Y / Y Y / / / Y 1,74 1 1,74 3 2. Режим короткого замыкания. На рис. Л2-8 изображена схема виртуальной установки. Рис. Л2-8. Модель и результаты моделирования трехфазного трансформатора большой мощности в режиме короткого замыкания. На рис. Л2-9 приведены действующие значения напряжений и токов первичной и вторичной обмоток и тока контура намагничивания. Рис. Л2-9. Результаты измерения действующих значений напряжений и токов первичной и вторичной обмоток и тока контура намагничивания трехфазного трансформатора большой мощности в режиме короткого замыкания представлены в таблице №Л2-5. На рис. Л2-10 изображены осциллограммы напряжений и токов первичной и вторичной обмоток и тока контура намагничивания исследуемого трехфазного трансформатора в режиме короткого замыкания. Рис. Л2-10. Осциллограммы кривых напряжений и токов первичной и вторичной обмоток и тока намагничивания трехфазного трансформатора большой мощности в режиме короткого замыкания для схемы соединения Y / Y . Подбираем такую величину входного напряжения, при которой по первичной обмотке “закороченного” трансформатора протекает номинальный ток. Результаты эксперимента сведены в таблицу №Л2-3. Таблица №Л2-3 Y / Y Y / / / Y Uk 18,3 Ik In 148,8 Pк 1928.9 18,3 148,8 1928.9 31,7 257,7 1928.9 31,7 257,7 1928.9 Определяем R1 и R2 : ( Y / Y , Y / ): R1 R2 Pk 1928,9 0, 04356Ом . 2 2 I n 2*148,82 ( / , / Y ): R1 R2 Pk 1928,9 0,131Ом 2 2 I n 2* 257, 7 2 Величины R1 и R2 математической модели составят: ( Y / Y , Y / ): R1 R2 Rbase * R1 p.u. 4,36*0, 01 0, 0436 Ом; ( / , / Y ): R1 R2 13,08*0,01 0,1308Ом. Ошибка в определении R1 и R2 : 0, 0436 0, 04356 *100% 0, 09%; . 0, 0436 0,131 0,1308 ( / , / Y ): *100% 0,15%. 0,131 ( Y / Y , Y / ): Определим значения L1 и L2 . Модуль комплексного сопротивления трехфазного трансформатора большой мощности в режиме короткого замыкания: U k 18,3 0,1232Ом; . I n 148,8 U 31, 7 0,3696Ом. ( / , / Y ): Z k k I n 257, 7 Индуктивное сопротивление короткого замыкания определится выражением: ( Y / Y , Y / ): Z k xk Zk2 Rk2 . Так как Rk 2 R1 2 R2 , то для различных типов соединений имеем: ( Y / Y , Y / ): xk ( L1 L2 ) 2 L1 2 L2 Zk2 4R12 0,12322 4*0,04362 0,087Ом; . ( / , / Y ): xk 0,36962 4*0,13082 0, 261Ом. 1.2.1.4.1.1 Отсюда 4 xk 0, 087 1,385*10 Гн; 2*2 f 2*2 *50 4 0, 261 4,16*10 Гн. ( / , / Y ): L1 L2 2* 2 *50 Величины L1 и L2 математической модели: ( Y / Y , Y / ): L1 L2 ( Y / Y , Y / ): L1 L2 L p.u. Lbase 0, 01*0, 0139 1,39*10 Гн; 4 ( / , / Y ): L1 L2 0, 01*0, 042 4, 2*10 Гн. 4 Ошибка в определении L1 и L2 : ( Y / Y , Y / ): 1,390*104 1,385*104 100 0 0 0, 4 0 0 ; 1,390*104 ( / , / Y ): 4, 20*104 4,16*104 100 0 0 0,9 0 0 . 4, 20*104 1.2.1.4.2 Найдем КПД трансформатора по формуле: P 96072, 26 н 100 100 97,8 0 0 . P1 98193, 66 3. Режим нагрузки. На рис. Л2-11 изображена схема виртуальной установки. Рис. Л2-11. Модель мощного трехфазного трансформатора в режиме активной нагрузки. Снимаем нагрузочную характеристику исследуемого трехфазного трансформатора большой мощности для его активного режима работы, регулируя сопротивление нагрузки в пределах: ( 0,8 Rн ), и для каждого из сопротивлений нагрузки определяем величину выходного напряжения. Результаты эксперимента сводим в таблицы № №Л2-4 и Л2-5. Таблица №Л2-4 Y / Y , / Y Iн[А] U[В] 0 380 31.5 379.1 65.5 378.1 146.8 375.7 257.9 372.5 308.3 371 Таблица №Л2-5 Y / , / Iн[А] U[В] 0 658.2 18.2 656.6 37.8 654.9 84.7 650.8 148.9 645.1 178 642.6 По данным этих таблиц на рис. Л2-12, Л2-13 построена нагрузочная характеристика исследуемого трехфазного трансформатора большой мощности. 381,00 380,00 379,00 378,00 U[В] 377,00 376,00 375,00 374,00 373,00 372,00 371,00 370,00 0,00 100,00 200,00 300,00 400,00 Iн[А] Рис. Л2-12. Нагрузочная характеристика мощного трансформатора при соединении его обмоток по схемам: Y / , / Y . трехфазного 660,00 658,00 656,00 654,00 U[В] 652,00 650,00 648,00 646,00 644,00 642,00 640,00 0,00 50,00 100,00 150,00 200,00 Iн[А] Рис. Л2-13. Нагрузочная характеристика мощного трехфазного трансформатора при соединении его обмоток по схемам: Y / , / Падение напряжения на трансформаторе равно: 660 13, 0 В; 380 660 13,1В; Y / : U (U 20 U 2н ) K т (658, 2 645,1) 658, 2 1143 22,8 В; / : U (U 20 U 2н ) K т (658, 2 645,1) 658, 2 1143 22, 6 В. / Y : U (U 20 U 2н ) K т (380 372,5) 380 Y / Y : U (U 20 U 2 н ) K т (380 372,5) или 13, 0 *100 3, 4%; 380 13,1 *100 2%; 658, 2 22,8 *100 3,5%; 658, 2 22, 6 *100 5,9%. 380 Y / Y : U расч Y / : U расч / : U расч / Y : U расч Расчет падения напряжения на трансформаторе с использованием выражения (1-13) дает следующие результаты: I н Rk 257,9*0, 0436* 2 0, 034; Uн 660 I x 257,9*0, 087 U kr н k 0, 034; Uн 660 Y / Y : U ka Y / : U ka I н Rk 148,9*0, 0436* 2 0, 020; Uн 660 I н xk 148,9*0, 087 0, 020; Uн 660 I R 148,9*0,1308* 2 0, 034; / : U ka н k Uн 1143 I x 148,9*0,1308* 2 U kr н k 0, 034; Uн 1143 I R 257,9*0,1308* 2 0, 059; / Y : U ka н k Uн 1143 I x 257,9*0, 261 U kr н k 0, 059. Uн 1143 U kr U % (U ka cos U kr sin ) 2 (U kr cos U ka sin ) 2 200 Y / Y : 12 (0, 034 cos 00 0, 034sin 00 ) 2 0 0 1(0, 034 cos 0 0.034sin 0 ) 0.034; 200 2 (U kr cos U ka sin ) 2 U % (U ka cos U kr sin ) 200 : Y / 12 (0, 020 cos 00 0, 020sin 00 ) 2 1(0, 020 cos 00 0.020sin 00 ) 0.020; 200 2 (U kr cos U ka sin ) 2 U % (U ka cos U kr sin ) 200 / : 12 (0, 034 cos 00 0, 034sin 00 ) 2 0 0 1(0, 034 cos 0 0.034sin 0 ) 0.034; 200 2 (U kr cos U ka sin ) 2 U % (U ka cos U kr sin ) 200 : / Y 12 (0, 059 cos 00 0, 059sin 00 ) 2 1(0, 059 cos 00 0.059sin 00 ) 0.059. 200 В процентах, по отношению к номинальному напряжению это составит: Y / Y : U %*100 0, 034*100 3, 4%; Y / : U %*100 0, 020*100 2, 0%; . / : U %*100 0, 034*100 3, 4%; / Y : U %*100 0, 059*100 5,9%. Величина ошибки при расчете падения напряжения на трансформаторе при соединении его обмоток по схеме / , рассчитанная по формуле (1-13), будет равна: 3,5 3, 4 *100 2,8%. 3,5 В остальных случаях соединений обмоток силового трехфазного трансформатора ошибка расчета падения напряжения при использовании этой формулы отсутствует. Определять величину падения напряжения на трансформаторе с помощью векторной диаграммы при такой малой величине падения напряжения (не выше 3%) нецелесообразно, т.к. точность этого метода невысока. Рассмотрим случай активно-индуктивной нагрузки при значении угла сдвига фаз между током и напряжением равном 720 (рис. Л2-14). Рис. Л2-14. Модель мощного трехфазного трансформатора в режиме активно-индуктивной нагрузки. Результаты расчетов сведены в таблицу №Л2-6. Таблица №Л2-6 U В 380 379 378,8 377,5 374,3 370,1 368,2 Iн А 0 27,7 33,2 68,9 154,1 270,2 322,5 Для случая активно-емкостной нагрузки при значении угла сдвига фаз между током и напряжением равном 720 (рис. Л2-15). Рис. Л2-15. Модель мощного трехфазного трансформатора в режиме активно-емкостной нагрузки. Результаты расчетов сведены в таблицу №Л2-7. Таблица №Л2-7 U В 380 380,5 380,6 381,2 382,8 385 386 Iн А 0 27,8 33,34 69,58 157,6 281 338,1 По данным таблиц №№Л2-6, Л2-7 на рис. Л2-16 построены нагрузочные характеристики трехфазного трансформатора большой мощности для случая активно-реактивной нагрузки. 390,00 U[В] 385,00 380,00 375,00 370,00 365,00 0,00 100,00 200,00 300,00 400,00 Iн[А] Рис. Л2-16 Нагрузочная характеристика трехфазного трансформатора большой мощности при активно-емкостной (1) и активно-индуктивной (2) нагрузках. Падение напряжения на трансформаторе индуктивном характерах нагрузки: при активно-емкостном и активно- 660 8, 68В; 380 660 U (U 20 U 2 н ) K т (380 370,1) 17,19 В 380 или в процентах 8, 68 U расч *100 2,3%; 380 17,19 U расч *100 4,5%. 380 Расчет падения напряжения на трансформаторе с использованием выражения (1-13): I x 281*0, 087 U kr н k 0, 037; Uн 660 I R 281*0, 0436* 2 U ka н k 0, 037; Uн 660 I x 270.2*0, 087 U kr н k 0, 036; Uн 660 I R 270, 2*0, 0436* 2 U ka н k 0, 036; Uн 660 U (U 20 U 2 н ) K т (380 385) U % (U ka cos U kr sin ) 2 (U kr cos U ka sin ) 2 200 12 [0, 037 cos(720 ) 0, 037 sin( 720 )]2 0 0 1[0, 037 cos(72 ) 0.037 sin( 72 )] 0, 024; 200 2 (U kr cos U ka sin ) 2 U % (U ka cos U kr sin ) 200 12 (0, 036 cos 720 0, 036sin 720 ) 2 1(0, 036 cos 720 0, 036sin 720 ) 0, 045; 200 В процентах, по отношению к номинальному напряжению это составит: U %*100 0, 024*100 2, 4%; U %*100 0, 045*100 4,5%; Величина ошибки при расчете падения напряжения на трансформаторе при соединении его обмоток по схеме / , рассчитанная по формуле (1-13), будет равна: 2,3 2, 4 *100 0, 043%. 2,3 В случае активно-индуктивной нагрузки трехфазного трансформатора ошибка в расчете при использовании этой формулы равна нулю. Используя модель исследуемого трансформатора, определяем зависимость КПД от тока нагрузки. Ввиду того, что дополнительные потери в трансформаторе (в ферромагнитном сердечнике и в обеих обмотках) не зависят от характера реактивной составляющей нагрузки (индуктивной или емкостной), а определяются лишь суммарным током нагрузки (активной и реактивной его составляющих), интересующая нас зависимость построена лишь для активного и активно-индуктивного характера нагрузки. Результаты исследования заносятся в таблицах: №Л2-8( активный характер) и №Л2-9( активно – индуктивный характер). Таблица №Л2- 1.2.1.4.2.1.1.1 8 P1 Вт 117313,7 98193,7 55959,5 25073,0 12170,2 10179,2 699,9 199,9 P2 Вт 114368,9 96072,3 55137,6 24749,3 11941,6 9959,3 499,9 0 I н А 308,3 257,9 146,8 65,5 31,5 26,3 1,36 0 % 97,5 97,8 98,5 98,7 98,1 97,8 71,4 0 Таблица №Л2-9 P1 Вт 40749 33924 19130 8560 4206 3537 1868 533 367 199,9 P2 Вт 375454 31616 18244 8223 3974 3315 1662 333 167 0 I н А 322,2 270,2 154,1 68,9 33,2 27,66 13,8 2,7 1,38 0 % 92,1 93,1 95,3 96,0 94,5 93,7 88,9 62,5 45,4 0 Зависимость КПД от тока нагрузки изображена на рис. Л2-17. 120,00 100,00 КПД% 80,00 1 2 60,00 40,00 20,00 0,00 0,00 -100,00 100,00 200,00 300,00 400,00 Iн[А] Рис. Л2-17. Зависимость коэффициента полезного действия трехфазного трансформатора большой мощности от тока нагрузки. (1-кривая, соответствующая режиму активной нагрузки, 2- активно реактивной нагрузки.) Лабораторная работа №3 Исследование трехфазной асинхронной машины с короткозамкнутым ротором 1. Цель работы – исследование трехфазной асинхронной машины с короткозамкнутым ротором. 2. Указания к выполнению работы. К выполнению лабораторной работы следует приступить после изучения разделов, посвященных трехфазной асинхронной машине, данного пособия. В качестве дополнительной литературы рекомендуется воспользоваться [Брускин]. 3. Содержание работы. 3.1 Определение параметров схемы замещения при помощи опытов холостого хода и короткого замыкания. 3.2 Снятие механической и рабочих характеристик машины в двигательном и генераторном режимах. 3.3 Снятие механических и рабочих характеристик машины в режиме скалярного управления скоростью. 3.4 Определение динамических параметров исследуемой асинхронной машины. 3.5 Определение КПД машины. Описание виртуальной лабораторной установки Виртуальная лабораторная установка представлена на рис. Л3-1. Рис. Л3-1. Модель трехфазной асинхронной машины с короткозамкнутым ротором. Она содержит: - источник переменного трехфазного напряжения Source из библиотеки Power System Blockset/Extras/Electrical Sources; - измеритель трехфазного напряжения и тока Three-Phase V-I Measurment (библиотека Power System Blockset/Extras/ Measurment); - исследуемая трехфазная асинхронная машина Asynhronous Machine (библиотека Power System Blockset/Extras/ Machines); - блок Display для количественного представления измеренных мощностей и блок Scope для наблюдения тока ротора и статора, а также скорости и момента асинхронной машины (главной библиотека Simulink/Sinks); - блок Step для задания механического момента на валу машины (главная библиотека Simulink/Source); - блок Display1 для количественного представления измеренных электромагнитного момента (Нм) и скорости (рад/c) машины (главная библиотека Simulink/Sinks); - блок Mux, объединяющий два сигнала в один векторный из главной библиотеки Simulink/Sygnal&System. Окно настройки параметров асинхронной машины показано на рис. Л3-2. Рис. Л3-2. Таблица настройки параметров асинхронной машины с короткозамкнутым ротором. В полях окна последовательно задаются: - тип ротора(Rotor Type), в выпадающем меню этого поля можно задать короткозамкнутый или фазный ротор; - система отсчета при анализе(Reference frame); - полная электрическая мощность, потребляемая в номинальном режиме, номинальное действующее линейное напряжение и частота; - параметры схемы замещения статора; - параметры схемы замещения ротора; - параметры ветви намагничивания; - момент инерции, коэффициент вязкого трения, число пар полюсов; - начальные условия для моделирования (скольжение, положение ротора, токи статора и их начальные фазы). Расчет параметров схемы замещения асинхронной машины Точный расчет параметров схемы замещения асинхронной машины, на основании ее паспортных данных, является весьма трудной задачей, так как ее момент связан с параметрами нелинейной зависимостью. Кроме того, сама электрическая машина является, по существу, системой с распределенными параметрами. Поэтому, используемая ниже методика не претендует на высокую точность расчета вышеуказанных параметров и основное ее назначение- задание параметров модели рассматриваемого двигателя с целью определения его характеристик. В качестве объекта исследования выбран асинхронный короткозамкнутый двигатель Ярославского электромеханического завода типа RA100LB4 с характеристиками, представленными в таблице №Л3-1. Таблица №Л3-1 Тип двля RA 100LB4 Масса Pн nн [кГ] [кВт] [об/мин] 3 24 1420 [%] cos 81 0.81 Iн [A] 7 Iк Iн 6.2 Mп Mн 2.2 M max Mн 2.6 J [кГ м 2 ] 0.0058 Используя данные этой таблицы, находим: 1). Величина номинального скольжения: n1 n2 1500 1420 0, 0533. n1 1500 2). Номинальная угловая скорость вращения ротора: n 1420 н 2 148, 7с 1. 30 30 3). Номинальный критический и пусковой моменты: sн Mн Pн н 3000 20,174 Нм. 148, 7 М max M н 2, 6* 20,17 52, 45 Нм. Мн М M п п M н 2, 2* 20,17 44,37 Нм. Мн M max 4). Индуктивное сопротивление ветви намагничивания: U U U 220 x' 53, 6Ом. I ан I н sin I н 1 cos 2 7 1 0,812 Индуктивность ветви намагничивания: x x 53,6 L'm 0,171Гн. 2 f 2 50 5). Активное сопротивление роторной цепи машины можно определить из выражения [Вольдек]: 1 sн 2 C12 R2' I ан Pн П мех . sн Точность определения механических потерь в машине П мех невелика. Поэтому на практике ее можно считать равной 1 5 0 0 мощности, потребляемой из сети [Ключев] (большие значения соответствуют двигателям меньшей мощности). Так как мощность рассматриваемого двигателя относительно невелика, то будем считать, что мощность механических потерь составляет 5% от полной мощности, потребляемой из сети. Коэффициент, учитывающий переход от Т- образной к Г- образной схеме замещения асинхронной машины, обычно лежит в пределах от 1,00 до 1,08, причем большие значения этого коэффициента соответствуют двигателям меньшей мощности. Поэтому и в этом случае выбираем большее значение коэффициента- 1,08. С учетом сказанного величина сопротивления роторной обмотки будет равна: P 3*0, 05UI н cos 3000 3*0, 05* 220*7 *0,81 R2' н 1,59Ом . 1 Sн 2 2 2 1 0, 0533 2 2 2 3*1, 08 *7 *0,81 * 3C1 I н cos 0, 0533 Sн 6) Считая, что часть магнитопровода асинхронной машины, по которой протекает основной магнитный поток, составляет (примерно) 50% от общего веса машины, из выражения Пст p1.0 / 50 B 2G [Костенко, ...] находим (приближенно) мощность потерь в ферромагнитном сердечнике машины: 1 Пст 3*1,52 * * 24 81Вт. 2 (Здесь удельная мощность потерь принята равной 4 [Костенко...], вес асинхронной шины согласно таблице №Л3-1- 24кГ, а магнитная индукция в магнитопроводе машины1,5 Тл.) Пренебрегая потерями в ферромагнитном сердечнике ротора и добавочными потерями в машине, можно считать, что мощность, выделяемая в активном сопротивлении статорной обмотки, определяется выражением: Пэл1 3UI н cos 1 0,05 108 3I н2 cos2 * R2' C12 3R12 I н2 cos2 . Отсюда находим величину R1 : R1 3UI н cos 1 0, 05 108 3I н2 cos 2 * C12 R2' 3I н2 cos 2 3* 220*7 *0,811 0,81 0, 05 108 3 7 *0,81 *1, 082 *1,59 2 3 7 *0,81 2 246, 04 2, 45Ом. 96, 45 (В математической модели не учитываются потери в ферромагнитном сердечнике статора асинхронной машины, поэтому коэффициент полезного действия на величину указанных потерь в модели будет выше, чем в реальной машине.) 7). Величину индуктивного сопротивления рассеяния статорной и роторной обмоток можно определить, воспользовавшись выражением для критического момента асинхронной машины: M max 3U н2 21С1 ( R1 R12 xк2 ) После подстановки в это выражение M max 52, 45Нм ; U н 220В ; 1 157с 1 ; C1 1, 08 ; R1 2, 45Ом и элементарных преобразований имеем: xк 5,16Ом . Если предположить, что индуктивности рассеяния статорной и роторной обмоток одинаковы, то можно найти их величины: xк 5,16 0, 008 Гн. 2* 2 *50 2* 2 *50 8). Коэффициент трения (friction factor) К тр определяется из принятого допущения, что 5% мощности, потребляемой из сети, приходятся на механические потери в машине: M н 0, 05* 20,17 К тр 6,8*103 Нмс. н 148, 7 9)Величину суммарного момента инерции, приведенного к выходному валу двигателя учетом момента инерции ротора, примем равной J 0, 058кГм 2 . 10)Число пар полюсов машины, согласно даням приведенной таблицы №Л3-1, равно 2. 11) Начальные условия выберем из предположения, что асинхронная машина отключена от питающей сети. В этом случае величина скольжения, очевидно, равна 1, а начальные значения токов статора и ротора асинхронной машины будут равны 0. 12). Индуктивность контура намагничивания связано с коэффициентом C1 следующей зависимостью [Вольдек]: C1 Lm L'm , отсюда находим индуктивность контура намагничивания: L'm 0,171 Lm 0,16 Гн. C1 1, 08 L1 L2 Рассчитанные параметры математической модели асинхронной машины типа 100LB4 представлены на рис. Л3-3. RA Рис. Л3-3. Параметры схемы замещения асинхронной короткозамкнутой машины типа RA 100LB4. 1.Режим холостого хода. На рис. Л3-4 представлена виртуальная модель асинхронной машины типа RA100LB4. Рис. Л3-4.Модель и результаты моделирования асинхронного короткозамкнутого двигателя типа RA100LB4, работающего в режиме холостого хода. На рис. Л3-5 изображены осциллограммы кривых токов статора и ротора, скорости ротора и момента на его валу, соответствующие режиму холостого хода. Рис. Л3-5. Осциллограммы кривых токов ротора, статора, скорости вращения ротора и момента на выходном валу асинхронного короткозамкнутого двигателя типа RA100LB4 в режиме холостого хода. В этом режиме можно определить механические и активные потери в обмотках двигателя. Первая составляющая этих потерь может быть определена переводом двигателя в генераторный режим. В результате эксперимента находим: П мех М вых 0 1,104 157,1 173, 4 Вт. Мощность потерь в обмотках двигателя может быть определена следующим образом: Пэл Пэл1 Пэл 2 PАхх PВхх PСхх 62,66 30, 22 26, 44 119,3Вт. Суммарные потери в режиме холостого хода, очевидно, определятся выражением: Пхх П мех Пэл 173, 4 119,3 192,7 Вт. Изменением значения опции “Final value”(рис. Л3-6) (в сторону отрицательных величин) блока “Step1” достигается выполнение условия равенства нулю выходного момента двигателя. Рис. Л3-6.Окно настройки параметров блока “Step”. 2. Режим нагрузки исследуемой машины. На рис. Л3-7 представлена виртуальная модель асинхронной машины типа RA 100LB4, соответствующая режиму нагрузки. Рис. Л3-7. Модель и результаты моделирования асинхронного короткозамкнутого двигателя типа RA 100LB4 в режиме нагрузки. На рис. Л3-8 изображены осциллограммы кривых переходных процессов токов ротора и статора, скорости вращения ротора, выходного момента, а также кривая нагрузки на валу машины. Рис. Л3-8. Осциллограммы кривых токов ротора, статора, скорости вращения ротора, момента на выходном валу и момента нагрузки асинхронного двигателя типа RA 100LB4 в режиме нагрузки. Определим экспериментально величину активного сопротивления ротора. При проведении этого опыта на выходной вал исследуемой машины была приложена номинальная нагрузка. Это позволит экспериментально определить величину активного сопротивления ротора. Из данных опыта находим, что при номинальной нагрузке имеем: M вых 21, 2 Нм; вых 149,8с 1; I sA 6,846 А; I sB 6, 625 А; I sC 6, 719 А. Используя зависимость между выходной мощностью машины и активным сопротивлением ротора, находим: PA PB PC 1233 1230 1235 cos 0,8325; U I sA I sB I sC 220 6,846 6,625 6,719 вых 157, 08 149,8 sн 0 0, 0463; 0 157, 08 R2 M вых вых I I I cos 1 s sн н 2 sA 2 sB 2 sC 2 21, 2 149,8 0463 6,846 6, 625 6, 719 *0,8325 * 1 0,0,0463 2 2 2 2 1,54Ом. Найдем ошибку в экспериментальном определении активного сопротивления ротора: 1,59 1,54 100 3,1 0 0 . 1,59 Определим индуктивность контура намагничивания, предварительно определив величину угла между током и напряжением в режиме номинальной нагрузки: sin 1 cos 2 1 0,83252 0,554 . Используя зависимость индуктивности контура намагничивания от параметров машины, находим: Lm 3U 3 220 0,173 Гн. C1 I sA I sB I sC 2 f sin 1,08 6,846 6,625 6,719 2 50 0,554 Найдем ошибку в экспериментальном определении индуктивного сопротивления контура намагничивания: 0,160 0,173 100 8, 6 0 0 . 0,160 Для определения активного сопротивления статора рассмотрим режим работы асинхронной машины с заторможенным ротором. 3.Режим работы с заторможенным ротором. На рис. Л3-9 представлена виртуальная модель асинхронной машины типа RA100LB, работающей в режиме с заторможенным ротором. Рис. Л3-9. Модель и результаты моделирования асинхронной короткозамкнутой машины типа RA 100LB4 в режиме работы с заторможенным ротором. На рис. Л3-10 изображены осциллограммы кривых переходных процессов токов ротора и статора, скорости вращения ротора и момента на его валу. Рис. Л3-10. Осциллограммы кривых переходного процесса изменения токов статора и ротора, скорости вращения и момента на выходном валу асинхронной короткозамкнутой машины типа RA 100LB4 в режиме работы с закороченным ротором. Для обеспечения такого режима работы осуществлена отрицательная обратная связь по выходному моменту асинхронного двигателя. В результате, согласно уравнению движения: d M Mc J , dt выходная скорость машины равна нулю. Очевидно, что в этом режиме вся энергия, потребляемая из питающей сети, расходуется на нагревание статорной и роторной обмоток, а механическая работа, совершаемая двигателем, равна нулю. Мощность, потребляемая исследуемым двигателем из питающей сети, определится выражением: Pвх PАк PВк PСк 7728 4928 5826 18482Вт . Эта мощность частично выделяется в статорной обмотке, а частично - в роторной, поэтому: R2 R1 I sA2 I sB2 I sC2 Pвх , отсюда: R1 Pвх 14228 R2 1,57 2,33Ом. 2 2 2 I I sB I sC 35,14 34,542 34, 66 2 2 sA Ошибка в экспериментальном определении сопротивления статорной обмотки: 2, 45 2,33 4,9 0 0 . 2, 45 Определим индуктивность рассеяния обмоток статора и ротора исследуемой машины. Для этого рассчитаем комплексное сопротивление статорной обмотки в режиме с заторможенным ротором: U 220 3 Zк 6,33Ом. I ср 35,14 34,54 34,66 Теперь можно найти реактивное сопротивление рассеяния статорной и роторной обмоток: xL1 xL2 Zк2 Rк2 6,332 3,92 5Ом, откуда: Lк xк 5 0, 00796 Гн. 2 2 2 f 2 2 50 Найдем ошибку в определении индуктивности рассеяния обмоток исследуемой машины: 0, 008 0, 00796 100 0,5 0 0 . 0, 008 Для определения активных потерь в двигателе в заторможенном режиме подберем такую величину напряжения питания, при которой по обмоткам статора протекают номинальные токи. В результате измерений получаем: U к 44 B; Пк PAк PВк PCк 192 183,6 193,5 569,1Вт. L1 L2 4.Механическая характеристика асинхронной машины. Для снятия механической характеристики необходимо предварительно обеспечить состояние исследуемой машины соответствующее режиму холостого хода, так как асинхронный тип машины переменного тока имеет область неустойчивой работы. Поэтому, в блоке “Step” виртуальной модели машины значение опции “Step time” примем равным такой величине, при которой оно будет больше времени переходного процесса разгона машины до скорости холостого хода. Экспериментально устанавливаем, что искомое время равно 0,35 секунды. После этого можно снять механическую характеристику асинхронной машины типа RA 100LB4. Результаты эксперимента сведены в таблицу №Л3-2. Таблица №Л3-2. M Нм n об / мин -122.6 -107.6 -97.67 -67.74 -57.76 -47.77 -17.8 0 1843.96 1771.4 1737.9 1661.6 1638.7 1616.7 1547 1500 Продолжение таблицы № Л3-2 M Нм n об / мин 11 41 54 35 1462.9 1319.7 1104.9 0 По данным таблицы на рис. Л3-11 построена статическая механическая характеристика асинхронной короткозамкнутой машины типа RA 100LB4. 2000,00 n[об/мин] 1500,00 1000,00 500,00 -150,00 -100,00 0,00 -50,00 0,00 50,00 100,00 M[Нм] Рис. Л3-11. Статическая механическая характеристика асинхронной короткозамкнутой машины типа RA 100LB4. 4. Исследование механических характеристик в режиме скалярного управления скоростью. Будем снимать механические характеристики исследуемой асинхронной машины с короткозамкнутым ротором соответствующие значениям входного напряжения и частоты, приведенным в таблице №Л3-3. Результаты экспериментов сведены в таблицы №№ Л3-4-Л3-7. Таблица № Л3-3 №№ п/п U B f 1 2 3 4 5 110 2 220 2 330 2 440 2 880 2 25 50 75 100 200 Гц Таблица № Л3-4(кривая 1) M Нм n об / мин -145 -139 -119 -99 -79 -40 0 20,5 30,5 36 30,7 999,8 987,4 953,0 923,4 895,7 834,6 750,6 671,3 594,9 461,2 0 Таблица № Л3-5(кривая 3) M Нм n об / мин -113 -98 -78 -58 -28 0 11,6 31,5 41,5 61,3 62,3 28,7 2678 2538 2461 2403 2325 2250 2245 2144 2096 1895 1859 0 Таблица № Л3-6(кривая 4) M Нм n об / мин -105 -78 -58 -28 0 12 32 42 52 62 67,8 23,8 3426 3225 3158 3075 2999 2964 2895 2851 2796 2708 2557 0 Таблица № Л3-7(кривая 5) -95 M Нм n об / мин -76 -56 -26 0 14 24 54 74 75,9 13,3 6369 6242 6164 6071 5999 5958 5926 5807 5626 5555 0 По данным этих таблиц на рис. Л3-12 построены искусственные механические характеристики исследуемой машины соответствующие различным значениям входного напряжения и частоты (кривая 2-естественная характеристика построена по данным таблицы № Л3-2). 8000,00 5 n[об/мин] 6000,00 4 4000,00 3 2 2000,00 1 0,00 -200,0 -150,0 -100,0 -50,00 0,00 0 0 0 50,00 100,00 M[Нм] Рис. Л3-12. Механические характеристики асинхронной машины с короткозамкнутым ротором типа RA 100LB4 в режиме скалярного управления скоростью(2- естественная характеристика; 1,3,4,5- искусственные характеристики). 5. Динамические характеристики исследуемой асинхронной машины. Исследуются два вида динамических механических характеристик: процесс разгона машины при подключении ее к питающему напряжению и при номинальном моменте на выходном валу (то есть при скачке управляющего воздействия) и при скачкообразном изменении возмущающего воздействия, в качестве которого служит момент нагрузки. Первый вид переходного процесса изображен на рис. Л3-12, а второй - на рис. Л3-13. Рис. Л3-12. Переходный процесс изменения момента и скорости при действии скачка управляющего воздействия по напряжению питания асинхронной машины типа RA 100LB4. Рис. Л3-13. Переходный процесс изменения момента и скорости при действии скачка возмущающего воздействия по моменту нагрузки на выходном валу асинхронной машины типа RA 100LB4. 6. Определение КПД исследуемой машины. Как известно, КПД машины определяется выражением: Pн 3000 80 0 0 . Pн Пхх Пк 3000 192, 7 569,1 Изменяя величину нагрузки машины, определим зависимость КПД от выходной мощности на валу машины. Результаты эксперимента сведены в таблицу №Л3-3. Таблица № Л3-3 Pвх Вт 0 450 769,7 1091,3 1916,9 3667 5581 7767 10585 Pвых Вт 0 156,4 467,4 776 1535 2996 4359 5560 6380 0 0 0 35 61 71,1 80 81,7 78 71,6 60 По данным этой таблицы на рис. Л3-14 построена интересующая нас зависимость. КПД[%] 90,00 80,00 70,00 60,00 50,00 40,00 30,00 20,00 10,00 0,00 0,00 2000,00 4000,00 6000,00 8000,00 Pвых[Вт] Рис. Л3-14. Зависимость КПД асинхронного короткозамкнутого двигателя типа RA 100LB4 от его выходной мощности. 1.2.1.4.2.1.1.2 1.2.1.4.2.1.1.3