УДК 538.935 Целью настоящей работы является выявление влияния электронной

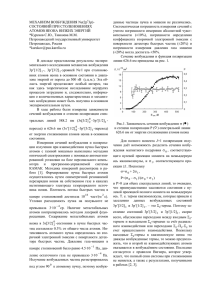
УДК 538.935
ВЫСОКОТОЧНАЯ ПРЕДСКАЗАТЕЛЬНАЯ ПОЛУЭМПИРИЧЕСКВЯ
ФОРМУЛА ДЛЯ СРЕДНЕЙ ЭНЕРГИИ ВОЗБУЖДЕНИЯ ПОЛУЧЕННАЯ
НА ОСНОВЕ МОДЕЛИ АТОМОВ ТОМАСА-ФЕРМИ
А.С. Бураков, Т.Х. Кат, В.А. Смоляр
Волгоградский государственный технический университет
400131 Волгоград пр. Ленина 28
(e-mail:smolar.v @yandex.ru)
Показано, что электронная конфигурация атомов существенно влияет на
зависимость величины средней энергии возбуждения I от атомного номера вещества Z в соответствии с расширенной периодической таблицей
элементов. Предложены формулы для вычисления средней энергии возбуждения с погрешностью не превышающей нескольких процентов, отражающие зависимости средней энергии возбуждения от атомного номера наблюдающиеся экспериментально и соответствующие периодам
этой таблицы элементов.
Целью настоящей работы является выявление влияния электронной
конфигурации атомов на зависимость средней энергии возбуждения от
атомного номера.
Теория
На зависимости I ( Z ) / Z от Z , показанной на Рис.1, видны участки
возрастания и спада, которые на участках возрастания соответствуют блокам s-g-f-d когда с увеличением Z заполняются глубокие оболочки атомов, а на участках спада – блоку p, когда заполняются внешние оболочки.
Здесь используется расширенная форма таблицы элементов, утвержденная Международным союзом теоретической и прикладной химии (IUPAC)
в качестве основной.
Ключевые слова: тормозная способность, формула Бете, модель атома
Томаса-Ферми, средняя энергия возбуждения.
Введение
В недавно опубликованном обстоятельном обзоре PDG (Particle Data
Group) [1] отмечается, что теоретическое вычисление средней энергии возбуждния вещества пролетающей заряженной частицей I ( Z ) является актуальной задачей, не решенной в настоящее время. В сводной таблице используемых
переменных в разделе «32. Passage of particles through matter »
переменная
I отмечена значком (Nota bene!). Самые общие оценки средней энергии воз-
буждения, как величины пропорциональной средней собственной частоте
атома, равной v / a , где v - скорости атомных электронов, a - размеры
атомов, показывают пропорциональную зависимость I от Z [2]. Однако
экспериментально измеренные величины I [3,4] обнаруживают более
сложную зависимость от Z .
Рис. 1. Средняя энергия возбуждения, отнесенная к одному электрону атома, по экспериментальным данным [3] (кружки с указанным интервалом погрешности), по формуле (7) (квадратики), по формуле (8) (крестики) и по эмпирическим формулам: - (9) сплошная линия, (10) штриховая линия.
В модели атома Томаса-Ферми определению средней энергии возбуждения соответствует средний логарифм энергии связи электронов на
где
расстоянии r от ядра Eb ( r ) , а число состояний с этой энергией соответ-
C
ствует числу электронов в слое dr на расстоянии r от ядра:
ln I 
1
Z


0
тической энергии
2
Ze
( r ),
2r
(2)
где  - функция экранирования поля ядра электронами, которая хорошо
аппроксимируется по Мольер выражением [4]
3
 ( x )   Bi exp    i x  ,
i 1
(3)
B1  0.1, B2  0.55, B3  0.35, 1  0.6, 2  1.2, 3  0.3 ,
1/3
Z d 2
.
4 r dr 2
Сравнение с экспериментом
Сравнение степенной зависимости средней энергии возбуждения
от атомного номера (5), (6), вытекающей из модели атома Томаса-Ферми,
с экспериментальными данными [2], рекомендованными ICRU [5], показывает, что эта зависимость соответствует областям быстрого роста
I ( Z ) / Z , когда с увеличением Z , когда заполняются глубокие оболочки
атомов s-g-f-d блоков. Величина коэффициента пропорциональности зависит от периода таблицы элементов, поэтому степенную зависимость (5)
можно записать в виде
I  Cn Z 4/3 ,
где x  r / 0.88534a0 Z , a9 - радиус Бора,. Подставляя в уравнение
Пуассона потенциал, выраженный через функцию экранирования (3), получаем плотность электронов в виде
n( r ) 
(6)
ln  Eb ( r ) n( r )4 r 2dr.
Энергия связи по теореме вириала [5] равна половине электроста-
Eb ( r )  
     d 2 
e2
exp   ln   2 dx   1.58 eV .
2  0.88534a0
 0  x  dx

(4)
Подставив выражения (2), (3) и (4) в (1) и выполнив интегрирование, и, затем потенцирование полученного выражения, получим
n
4
5
6
7
Z
19  30 37  48 55  80 87  112
Cn , eV 3.68
2.86
2.34
2.16
где Cn найдены подгонкой формулы (7) к экспериментальным данным
[4], по порядку величины соответствуют оценке методом Томаса-Ферми,
и с ростом Z , как и следовало ожидать, приближаются к этой оценке.
Каждый из периодов, начиная с третьего, заканчивается p – бло-
I
  d  
Ze
exp   ln   2 dx   CZ 4/3 ,
2b
 0  x  dx

2
2
(5)
ком с шестью атомами, для которых рост I ( Z ) / Z с увеличением Z сменяется спадом. На участках спада также можно применить степенную зависимость, показатель которой оказывается равным ½:
(7)
I  Cn Z 1/2 ,
n
3
4
5
6
7
.
Z
11  18 31  36 49  54 81  86 113  118
Cn , eV 44.7
59.8
67.8
89.4
110
(8)
11.2  11.7 Z ,
I , eV  
 52.8  8.71Z ,
Z  13,
Z  13.
(10)
Отклонение величин I ( Z ) , вычисленных по формулам (7), (8) с коэффи-
Однако эти эмпирические формулы не отражают периодических свойств
циентами пропорциональности, найденными подгонкой к величинам I ,
рекомендованным ICRU (International Commission on Radiation and Measurements) [4], не превышает нескольких процентов. На интервале атомных
номеров, представленных в таблицах [3] ( Z  [4,100] ), среднее относи-
зависимости I ( Z ) / Z от Z , и, как можно видеть из Рис.1, не так точно,
как предлагаемые нами формулы (7) и (8), аппроксимируют зависимость
средней энергии возбуждения от атомного номера. Кроме того, эти формулы дают величины средней энергии возбуждения еще не открытых, но
теоретически предсказанных тяжелых нестабильных элементов [8].
тельное отклонение близко к нулю
M
1 100 ( I ICRU ( Zi )  I ( Zi ))
 3.5  104

97 i 4
I ICRU ( Zi )
Выводы
,
Модель атома Томаса-Ферми позволяет, исходя из первых принципов, понять причину периодических возрастаний и спадов зависимости
а дисперсия составляет всего 0.2%

I ( Z ) / Z от Z , связав эту зависимость с заполнением оболочек атома,
2
 ( I ICRU ( Zi )  M ) 
1


  0.002 ,
96  97 i 4 
I ICRU ( Zi ) 
100
которое отражено в таблице элементов, построенной по квантовомеханическому принципу. вленных при увеличении Z электронов.
где I ICRU ( Z ) - рекомендованные ICRU величины средней энергии возбуждения. Малые величины среднего относительного отклонения и дисперсии подтверждают высокую точность, с которой предлагаемые формулы представляют рекомендованные ICRU величины средней энергии
возбуждения.
Для вычисления средний энергии возбуждения атома часто используют
эмпирическую формулу (Berger and Seltzer, 1964 [6] )
(9.76  58.8Z 1.19 ) Z , Z  13,
I , eV  
11.5, Z  12;

а также формулу (Dalton and Turner, 1968 [7])
(9)
Модель атома Томаса-Ферми дает описание степенной зависимостью I  Cn Z
средней энергии возбуждения при заполнении s-g-f-d
блоков этой таблицы элементов.
4/3
Модель атома Томаса-Ферми позволяет предложить новые физически обоснованные и более точные формулы для зависимости средней
энергии возбуждения от атомного номера.
Литература
1. K.A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014).
2.Л.Д. Ландау, Е.М. Лифшиц, Квантовая механика, т.3, М.: Наука (1963).
3. S.M. Seltzer and M.J. Berger, Int. J. of Applied Rad. 33, 1189 (1982).
4. M.,J. Berger, M. Inokuti, H.,H. Anderson et al., Stopping Powers for Elec
trons and Positrons, ICRU Report 37, (1984)
5. Б.В. Васильев, В.Л. Любошиц, УФН, 164, 367 (1994).
6. M.J. Berger,S.M. Seltzer, Studies in Penetration of Charged Particles in Matter. Nuclear Science Series Report No. 39, NAS-NRC Publication No. 1133,
National Academy of Science, Washington, DC, 205 (1964.
7. P. Dalton, J.E. Turner Helth Phys. 15, 257 (1980).
8. Pekka Pyykkoe, Phys. Chem. Chem. Phys., 13, 161 (2011).
High-precision predictive semi-empirical formula of the mean excitation
energy on the basis of the Thomas-Fermi model of atoms
A. S. Burakov, Tran Hai Kat, V. A. Smolar
It is shown that the electronic configuration of atoms significantly affect the dependence of the average excitation energy from atomic number
substances Z in accordance with the extended periodic table of the elements. The proposed formula gives the value of the mean excitation energy
with high precision.
Keywords: mean excitation energy, stopping power, Bethe formula, atom
model Thomas-Fermi