КПД пушки Гаусса

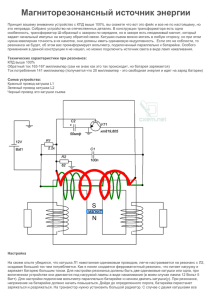
КПД пушки Гаусса
Курмашев Андрей, 10 класс МАОУ «Гимназия г.Троицка» Московская область
Среди школьников очень популярна идея изготовления электромагнитной пушки (пушки
Гаусса). Изготовленные образцы обычно малоэффективны, и не оправдывают ожиданий своих
создателей. Понимание физики выстрела помогло бы в конструировании более эффективных пушек. В
данной работе я попытался оценить возможный КПД установки теоретически, и проверить свою оценку
на практике.
В качестве модели пушки я рассматривал отрезок соленоида (катушку) длиной L, вдоль оси
которого, без трения может скользить тонкий ферромагнитный стержень. Магнитное поле катушки
намагничивает стержень в направлении вектора магнитной
индукции
. Я считал, что величина
возникающего магнитного момента участка стержня длиной
и длине самого участка
(нет насыщения).
пропорциональна величине вектора
Магнитное поле отрезка соленоида на оси неоднородно. В неоднородном поле на магнитный
момент будет действовать сила, модуль которой пропорционален, как величине момента, так и
скорости изменения магнитного поля вдоль оси.
Применяя законы Био-Савара-Лапласа и принцип суперпозиции, можно вычислить модуль
вектора магнитной индукции и его производные на оси катушки радиуса R и длины L. Вывод, из-за его
громоздкости, я не привожу. Подставляя результаты расчётов в предыдущее равенство, получим
Для удобства анализа я преобразовал предыдущую формулу к такому виду, чтобы в него входили
безразмерные длины
На рис.1 представлено семейство кривых – графиков зависимостей удельной силы, действующей на элемент
снаряда от расстояния от края катушки, нормированного на её радиус. Параметром кривых является
отношение длины катушки к её радиусу.
Рис.1
Можно отметить следующие особенности показанных кривых: кривые имеют симметрию,
характерную для нечётных функций (это и неудивительно, т.к. стороны катушки равноправны, и
снаряд, пройдя середину, будет втягиваться внутрь); кривые имеют максимум, положение которого
относительно края катушки определяется отношением L/R (при L/R>1 положение максимума внутри
катушки, а при L/R<1 – вне катушки); чем «тоньше» катушка, тем больше удельная сила в максимуме
(бесконечно тонкий виток провода описывается «граничной кривой», к которой стремятся кривые при
малых L/R); удельная сила резко уменьшается на расстояниях 1,5R – 2R от края катушки.
Допустим, небольшой снаряд длиной
ускоряется неоднородным полем. Согласно моей
модели, с точки зрения эффективности, ускорение снаряда должно производиться от положения на
расстоянии в несколько R от края катушки до её центра (где сила меняет знак). Причём толщина
катушки должна быть как можно меньше. Чтобы показать справедливость модели, мною была
изготовлена электромагнитная пушка, эскиз которой изображён на рис.2.
Рис.2
В качестве направляющей была использована полиэтиленовая труба, катушка намотана
медный проводом диаметром d=1,2мм в K=60слоёв по N=100 витков в каждом, в качестве снаряда
использовался стальной стержень длиной s=133мм и массой m=49г. Импульс тока в катушке с активным
сопротивлением обмотки r=7,2Ом возникал при разрядке конденсатора ёмкостью C=2500мкФ,
заряженного до напряжения U=260В. Для оценки эффективности пушки измерялась дальность стрельбы
с возвышения h=50,3см. Время падения снаряда τ определяется высотой h, а дальность полёта X
скоростью вылета v
X  v   v 
2h
g
 vX
g
2h
Кинетическая энергия, сообщённая снаряду
E
mv2
mg
 X2
2
4h
Электрическая энергия, запасённая в конденсаторе
СU 2
W
2
Разделив последнее равенство на предпоследнее, получим выражение для КПД

Е
mg
 X2
W
2hCU 2
Я устанавливал в трубе на расстоянии z (см. рис.2) от её края снаряд, и, рассчитывая по такой формуле КПД ,
получил зависимость КПД от начального положения снаряда, который представлен на рис.3
Рис.3
Как видно по графику, КПД максимально при такой закладке на снаряда, при которой его центр будет внутри
катушки. Для соотношения L/R=2,2, характерного для данной катушки, именно там находится максимум
удельной силы. При выдвигании стержня из катушки КПД резко падает, что иллюстрирует график Рис.1