5 - RTU DF

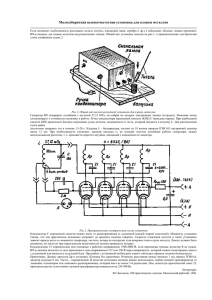
Лабораторная работа N5.
КАТУШКА СО СТАЛЬНЫМ СЕРДЕЧНИКОМ
Цель работы - ознакомление с эквивалентной схемой катушки, ее векторной диаграммой, а также выяснение влияния материала и конструкции сердечника на потери активной
мощности.
5.1. Общие положения
5.1.1. Теоретические пояснения
Изготовление катушек со стальными сердечниками( катушка "со сталью") обусловлено
специфическими свойствами железа - его высокой магнитной проницаемостью, что позволяет усиливать (до тысячи раз) магнитный поток при одной и той же магнитодвижущей
силе, сосредотачивать его в определенной области пространства и придавать ему определенную конфигурацию. В катушке со сталью различают главный магнитный поток Ф 0, линии которого замыкаются через стальной сердечник, и. поток рассеяния Фs, линии которого замыкаются через воздух. Эквивалентная схема катушки со сталью приведена на
рис.5.1.
а)
б)
Рис.5.1. Катушка со стальным сердечником.
(а-эквивалентная электрическая схема, б-векторная диаграмма.)
Потери в обмотке катушки Роб учитываются сопротивлением Rоб и Pоб=I2Rоб. Часть
энергии теряется на перемагничевание стали (потери на гистерезис P Г) и на вихревые
токи (Рв), эти потери учитываются активной проводимостью g0.
1
С главным магнитным потоком связывают основную индуктивную проводимость b0,
а с потоком рассеяния индуктивное сопротивление Xs.
Дальнейшие соотношения приведем в приближении замены несинусоидальных токов,
напряжений, индукций, потоков эквивалентными синусоидальными функциями. Тогда
 
 
U=IRоб+jXsI+Uф
(5.1)
Т.к. поток Ф в катушке со сталью не пропорционален протекающему по ней току, то
вместо соотношения
uL
di
dt
следует пользоваться уравнением
u
d
dФ
w
,
dt
dt
где Ф=Фмsint, Фм-амплетуда, t-время, =2πf-угловая частота .
В рассматриваемом случае
u ф  w1
dФ0
d


 w1 Ф0 м sin t   w1Ф0 м cos t  w1Ф0 м 2f sin  t   .
dt
dt
2

из формулы видно, что напряжение опережает поток на
значениям с учетом, что
2
2

. Переходя к действующим
2
 4.44 , получим
U   w1
Ф0 м 2f
2
 4.44 fФ0
или
U ф  4.44 w1 fSB0
(5.2)
где В0-действующее значение магнитной индукции,Тл, S-сечение магнитопровода
(сердечника).
На рис.5.1б приведена векторная диаграмма катушки со сталью. Потери в стали P м
характеризуются величиной tg и рассчитываются по формуле:
2
Рм=Рг+Рв=Р-Роб=UфI0=UфIsin=Uфg0
(5.3)
Реактивная намагничивающая мощность определяется по формуле :
2
Q=UфIф=UфIcos=Uфb0
2
(5.4)
Потери энергии на гистерезис Рг пропорциональны объему сердечника, первой степени частоты и площади гистерезисной кривой. Потери на вихревые токи Р в пропорциональны квадрату амплитудного значения индукции, квадрату частоты и квадрату толщины магнитопровода при постоянной ширине. Для уменьшения потерь Р в сердечники изготавливают из тонких изолированных друг от друг листов, а для уменьшения потерь Рг используют магнитомягкие материалы, у которых площадь гистерезиса мала. Для различных марок электротехнических сталей в справочниках приводятся зависимости
Q0(Bм)=Q/G и P0(Bм)=Pм/G или tg(Bм), где G вес сердечника, Вм амплитуда магнитной
индукции, Тл.
Значение Uф может быть определено, если на сердечник, по которому замыкается
главный поток Ф0, намотать вторичную обмотку с числом витков w2 и измерить величину
наведенной Э.Д.С. U2; тогда
Uф U2w1/w2
(5.5)
5.1.2. Схема эксперимента
Схема эксперимента приведена на рис.5.2. Исследуются свойства катушки w1, на одном каркасе с которой намотана другая катушка w2, причем w1=w2=w. В каркас могут
быть введены сердечники различных, типов: стальной монолитный, стальной листовой,
латунный.
Если измерения проводить с катушкой без сердечника, когда ветвь с g0 отсутствует,
то по показаниям приборов W, A, V1 можно определить сопротивление обмотки Rоб:
Rоб=Zcosφ , где Z=U/I ; соsφ=Р/UI.
(5.6)
Значение индуктивности рассеяния для катушки с сердечником определяется в процессе построения векторной диаграммы на основе показания приборов W, V1, A1, V2 и
рассчитанного значения Rоб. Угол потерь определяется также по векторной диаграмме.
Рекомендуется следующая последовательность построения векторной диаграммы:

строится вектор I, модуль которого указан амперметром А, а фаза принимается равной нулю;

под углом φ к вектору I(соsφ=Р/UI, где P,U,I соответствуют показаниям приборов W,

V1, А) откладывается вектор напряжения U, подведенного к катушке;
3



из конца вектора U строится вектор (-RобI) параллельно I;

из начала вектора RобI перпендикулярно к нему проводится линия, указывающая нап
равление вектора jXsI, а из точки начала вектора U проводится дуга радиусом Uф, равным
показанию вольтметра V2, до пересечения с перпендикуляром; в результате будут


определены длина вектора jXsI и направление вектора Uф, кроме того можно рассчитать
значение сопротивления Хs;


под углом (-/2) к вектору Uф откладывается вектор потока Ф0, модуль которого
равен Uф/w1;


векторы токов I0 и Iф, а также угол  будут определены в результате восстановления


перпендикуляра из конца вектора I к направлению вектора Ф0.
Рис.5.2. Схема эксперимента.
5.2. Предварительная подготовка
В процессе подготовки к работе следует внимательно разобраться с эквивалентной
схемой катушки со сталью и способами определения ее элементов. Необходимо оформить
разделы: "теоретические положения" (привести основные расчетные формулы), "схема
эксперимента", а также заготовить таблицы для занесения результатов.
5.3. Экспериментальная и расчетная часть
Собрать схему эксперимента и записать значения:
w = ______________ витков, S = ______________ кв.м., f = _______________Гц.
Провести измерения для катушки без сердечника и при трех различных сердечниках,
занося результаты в таблицу по форме табл.5.1. Измерения проводить при одном и том же
значении тока I=1A. Для каждого опыта рассчитать потери мощности в сердечнике Pм.
.
4
Таблица 5.1.
Исследование зависимости потерь мощности от материала сердечника
№ опыта
1.
2.
3.
4.
Тип сердечника
U,V
I,A
Uф,V
Р,W
Рм=Р-I2Rоб,W

Сталь-монолит
Сталь-листовая
Латунный
Рассчитать величину сопротивления обмотки: Rоб =_________Ω
Построить векторные диаграммы для опытов 2 и 3 и рассчитать параметры
эквивалентной схемы катушки; результаты свести в таблицу по форме табл.5.2.
Исследовать зависимость потерь мощности Pм, в массивном стальном сердечнике от
магнитной индукции при изменении тока от 0 до 1A. Результаты измерения и обработки
занести в таблицу по форме табл.5.3. Зависимость Pм(В) представить в виде графика.
5.4. Анализ результатов
Объяснить характер зависимости потерь мощности в сердечнике от материала
сердечника по результатам опытов и отметить степень согласия с физическими
представлениями.
Обсудить соответствие экспериментально полученной зависимости P м(В)
теоретическим выводам.
Таблица 5.2
Расчет параметров эквивалентной схемы катушки со сталью
Парметр и формула
для расчета
Us,V по векторной
диаграмме
Xs=Us/I,Ω
Uф,V показания V1
I,A показания A
δ,град, из векторной
диаграммы
g0=(I/Uф)sinδ
b0=(I/Uф)cosδ
Ф0= U ф 2 /( w1 )

Катушка со
сталью-монолит

Фs= X s I 2 / w1 
5
Катушка со
сталью листовой
Таблица 5.3.
Исследование зависимости Pм(В)
Измеряемые и расчетные параметры
Значения тока, подводимого к катушке I,A
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Uф, V (V2)
P, W (W)
Рм=Р-I2Rоб
В=Uф/(4.44fw1S),Т
5.5. Перечень контрольных вопросов
1. Как определить потери мощности в обмотке катушки?
2. Как определить потери мощности в стальном сердечнике катушки?
3. Как в данной схеме осуществить изменение индукции в стальном сердечнике?
4. Каков будет ток в катушке, если сравнивать катушку со со стальным сердечником и
катушку без сердечника при том же напряжении?Что сделать, чтобы в обоих
случаях значение тока было одно и то же?
5. Нарисовать эквивалентную схему катушки со сталью и объяснить, какие процессы
в реальной катушке характеризует каждый элемент?
6. Юбъяснить порядок расчета параметров эквивалентной схемы и порядок
построения векторной диаграммы.
7. Зависят ли параметры эквивалентной схемы катушки со сталью от значения
напряжения питания?
8. В случае какого сердечника поток рассеяния катушки больше при одном и том же
значении тока?
6