Расчет параметров ключевого смесителя

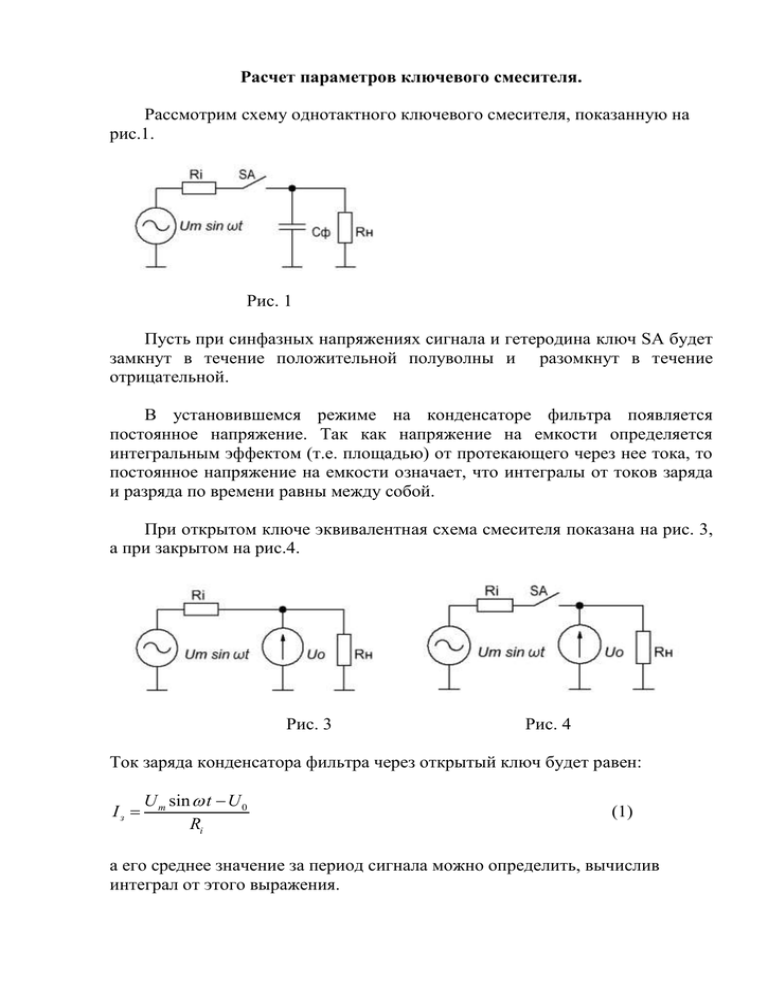
Расчет параметров ключевого смесителя.
Рассмотрим схему однотактного ключевого смесителя, показанную на
рис.1.
Рис. 1
Пусть при синфазных напряжениях сигнала и гетеродина ключ SA будет
замкнут в течение положительной полуволны и разомкнут в течение
отрицательной.
В установившемся режиме на конденсаторе фильтра появляется
постоянное напряжение. Так как напряжение на емкости определяется
интегральным эффектом (т.е. площадью) от протекающего через нее тока, то
постоянное напряжение на емкости означает, что интегралы от токов заряда
и разряда по времени равны между собой.
При открытом ключе эквивалентная схема смесителя показана на рис. 3,
а при закрытом на рис.4.
Рис. 3
Рис. 4
Ток заряда конденсатора фильтра через открытый ключ будет равен:
Iз 
U m sin  t  U 0
Ri
(1)
а его среднее значение за период сигнала можно определить, вычислив
интеграл от этого выражения.
I з ср 
2U m   U 0
2 Ri
(2)
С учетом того, что ток разряда не зависит от состояния ключа и
происходит равномерно в течение всего периода, среднее значение тока
разряда через нагрузку будет равно:
I р ср 
U0
Rн
(3)
Из условия постоянства напряжения на конденсаторе фильтра составляем
уравнение токов:
2U m  U 0 U 0

2 Ri
Rн
(4)
из которого определяем выходное напряжение смесителя:
U0 
2U m

Rн
Rн  2 Ri
(5)
Мощность в нагрузке будет равна:
U 02 4U m2
Rн
P0 
 2
Rн
 ( Rн  2 Ri )2
(6)
Сопротивление нагрузки, при котором выходная мощность будет
максимальной можно найти, если взять производную от выражения (6) по
переменной Rн и приравнять ее к нулю. Решив полученное уравнение
относительно Rн получим значение оптимального сопротивления нагрузки:
Rн опт  2 Ri
(7)
При оптимальном сопротивлении нагрузки выражения (5) и (6) упрощаются
до вида:
U0 
Um

U m2
U m2
P0  2

 Rн опт 2 2 Ri
(8)
(9)
Посмотрим, как меняется выходная мощность при изменении сопротивления
нагрузки. При Um=1 В и Ri=50 Ом эта зависимость показана на рис 5.
Рис. 5
Как видим, зависимость имеет достаточно слабо выраженный максимум.
При изменении сопротивления нагрузки в два раза от оптимальной величины
(50 или 200 Ом), выходная мощность уменьшается всего лишь в 1,125 раза
или на 0,5 дБ. А для того чтобы выходная мощность изменилась в два раза
или на 3 дБ, сопротивление нагрузки должно измениться в 5,83 раза от
оптимального, при этом его значения будут равны 17 или 583 Ома.
Зная оптимальное сопротивление нагрузки легко рассчитать
коэффициенты передачи смесителя по напряжению и по мощности.
Коэффициент передачи по напряжению будет равен:
Kн 
U0 1
  0,318  9,94 дБ
Um 
(10)
Коэффициент передачи по мощности определяется как отношение выходной
мощности к максимальной эффективной мощности источника сигнала:
Kр 
2 P0 1

 0,101  9,94 дБ
Pm  2
(11)
Как видим при Q=2 и работе смесителя на согласованную нагрузку его
коэффициенты передачи по напряжению и по мощности равны между собой.
Причем эти значения для Q=2 являются максимально возможными, т.к. в
данном смесителе отсутствуют потери.
Входное сопротивление смесителя по схеме на рис. 1 можно найти,
если определить входные сопротивления схем на рис. 3 и 4.
Входное сопротивление смесителя при открытом ключе можно
определить как отношение среднего напряжения на выходе источника к его
среднему току. Формы напряжения и тока источника показаны на рис. 6 и 7
соответственно.
Рис. 6
Рис. 7
Средний ток источника из (2) нам уже известен, а среднее за период
напряжение при открытом ключе будет равно Uo/2. Отсюда среднее за
период входное сопротивление смесителя будет равно:
Rвх ср 
U ср
I ср

U 0 2U m   U 0
/
 Ri
2
2 Ri
(12)
Как видим, при оптимальном сопротивлении нагрузки и идеальном
ключе, согласование входного сопротивления смесителя с источником
сигнала также является идеальным.
Входное сопротивление можно выразить и через сопротивление
нагрузки. Найдя Ri из (7) и подставив его в (12) получим:
Rвх 
Rн опт
2
Проведение ряда аналогичных вычислений позволило найти
зависимость полученных выше соотношений от скважности.

 2
Q 1  cos 
U
Q
U0  m 

4




 2  
Q
1

cos

 Q 
U m2



Р0  2
 Ri
16
(13)
2
(14)
Rнопт  QRi
(15)

 2  
Q  1  cos 

1 
 Q 
Кн 

4

 2  
Q  1  cos 

1 
 Q 
Kp  2

8
(16)
2
(17)
Rвх  Ri
(18)
Из (18) видно, что входное сопротивление смесителя не зависит от
скважности и согласование смесителя с источником сигнала получается
идеальным, если согласован выход смесителя с нагрузкой.
На рис. 10 показано, как меняются коэффициенты передачи смесителя
в зависимости от скважности.
Рис. 10
Из графиков видно, что коэффициент передачи по мощности при
скважности, которая выражается целым числом, имеет максимальное
значение при Q = 2 и небольшой максимум, превышающий это значение на
0,245 дБ при Q = 2,255. При Q = 4 коэффициент передачи по мощности
падает на 3 дБ по сравнению с коэффициентом передачи при Q = 2.
Коэффициенты передачи по напряжению и мощности при Q = 2 равны
между собой, а коэффициент передачи по напряжению имеет максимум при
Q = 2,695, который равен -8,818 дБ и одинаковые значения при Q = 2 и Q = 4,
которые равны -9,94 дБ.
Из рис. 10 можно сделать и еще один вывод. Сравнивать напрямую
эффективность работы смесителей по коэффициенту передачи по
напряжению можно только в одном случае, если равны их оптимальные
сопротивления нагрузки. Если равенства нет, то тогда сравнение возможно
только в совокупности с отношением их оптимальных сопротивлений
нагрузок. Например, в нашем случае для сравнения эффективности работы
смесителей при Q=2 и Q=4 коэффициент передачи по напряжению при Q=4
нужно уменьшить на 20log 2 / 1  3дБ . Другими словами отношение
коэффициентов передачи по напряжению нужно привести к отношению
коэффициентов передачи по мощности. А еще лучше, чтобы вообще не
упоминать о сопротивлениях нагрузки, сравнивать эффективность работы
смесителей только по коэффициенту передачи по мощности.
Рассмотрим работу смесителя в асинхронном режиме. В соответствии с
[1] если фазу опорного сигнала поменять на 180°, то выходное напряжение
поменяет полярность, так как ключ будет пропускать только отрицательные
полуволны входного напряжения. Если сдвиг по фазе будет равен 90°, то ключ будет пропускать и положительные и отрицательные полуволны и на
выходе смесителя сигнал будет равен нулю, Анализ схемы устройства при
произвольном фазовом сдвиге приводит к выводу, что на выходе смесителя в
этом случае сигнал будет равен:
U вых 
1

U m cos( )
Если напряжения сигнала и гетеродина различаются по частоте, то
тогда фазовый сдвиг между этими сигналами будет равен:
  (c  0 )t
В результате на выходе смесителя получается не постоянное, а переменное напряжение разностной частоты, мгновенное значение которого
будет определяться выражением:
U вых 
1

U m cos((c  0 )   )
Как видим, амплитудное значение выходного напряжения равно
выходному напряжению при синфазном сигнале, соответственно и
коэффициент передачи по напряжению (16) останется без изменений.
Несколько иначе обстоит дело с выходной мощностью. Она будет
равна:
Pвых
2
U вых
U m2

 2 cos2 ((c  0 )   )
Rн
 Rн
На рис. хх показана новая ситуация с мощностью на выходе смесителя.
Рис. хх
Как видим, максимальная амплитуда выходной мощности разностной
частоты достигает уровня мощности при синфазном сигнале, но при этом
средняя ее величина будет в два раза меньше. Соответственно и коэффициент
передачи по мощности уменьшится вдвое. При Q=2 он будет равен:
P
1
K р  вых  2  0,050  12,95 дБ
Pm 2
А в общем виде его величина будет равна:

 2
Q 1  cos 
1
 Q
Kp  2 

16



2
Выражения для оптимального сопротивления нагрузки (15) и входного
сопротивления (18) остаются без изменений.
Если рассмотреть работу смесителя при количестве фаз больше одной,
то все полученные ранее соотношения (13-18) остаются в силе, ведь фазы
работают поочередно и при идеальном ключе не влияют друг на друга.
Входное сопротивление многофазного смесителя при оптимальной нагрузке
в каждой фазе будет равно входному сопротивлению отдельно взятой фазы
поочередно подключаемой к нагрузке. Единственное что изменится это
суммарные показатели. При двухфазном смесителе они увеличатся вдвое.
Коэффициент передачи по напряжению будет равен:
Kн 
2

 0,636  3,92 дБ
а коэффициент передачи по мощности:
Kр 
2
2
 0, 202  6,93 дБ
Эти значения будут являться теоретически максимально возможными и
для балансной схемы смесителя.
Зависимость суммарных коэффициентов передачи от числа фаз
смесителя при условии, что n = Q показана на рис. х.
Рис. х
Из графиков видно, что максимальный суммарный коэффициент
передачи по мощности будет равен -5,9 дБ при трехфазной схеме.
Двухфазная и четырехфазная схемы имеют одинаковые суммарные
коэффициенты передачи равные -6,93 дБ.
Суммарный коэффициент передачи по напряжению при двухфазном
смесителе будет равен -3,92 дБ, при трехфазном +0,62 дБ, при
четырехфазном +2,09 дБ и далее монотонно растет, асимптотически
приближаясь к своему пределу +3,92 дБ. Рассматривая суммарный
коэффициент передачи по напряжению нужно помнить о том, что
алгебраическая сумма выходных напряжений многофазного смесителя равна
нулю.
1. Петин Г.П. Ключевой синхронный детектор.