Делицын Л.Л.
реклама

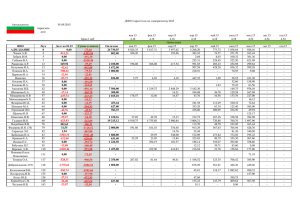
МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ НОВОВВЕДЕНИЯ С УЧЕТОМ РАСПРЕДЕЛЕНИЯ РАЗМЕРОВ ДОМОХОЗЯЙСТВ Л.Л. Делицын Московский Государственный Университет Культуры и Искусств, г. Химки, Россия MODELING IMPACT OF HOUSEHOLD SIZE DISTRIBUTION ON INNOVATION DIFFUSION L.L. Delitsin Moscow State University of Culture and Arts, Khimki, Russia В работе построена количественная модель распространения инноваций, которая описывает и объясняет результаты социологических опросов о личном владении новинкой, об использовании новинки, о наличии ее в семье. В качестве примера нововведения выбрана сотовая связь, поскольку результаты опросов о ее распространении в России регулярно публикуются с 2000 г. Данные опросов об использовании мобильной связи и владении сотовыми телефонами, проведенных пятью организациями, изображены на рис.1. Отметим, что опрашивались только взрослые россияне. C целью построения количественной модели, объясняющей данные опросов, используем четыре допущения: 1) Условный “глава семейства” первоначально приобретает новинку для себя, он является ее владельцем. 2) Период времени между приобретением семьей мобильного терминала и началом использования этого устройства всеми взрослыми членами пренебрежимо мал. Это предположение позволяет использовать данные об использовании новинки и данные о наличии новинки в семье как эквивалентные. Как показывает рис.1, данные опросов подтверждают такое предположение. 3) На решение взрослого россиянина о покупке нововведения влияет доля пользователей сотовой связи среди взрослого населения, которую он оценивает в процессе межличностных коммуникаций, кроме того воздействие оказывают массовые коммуникации (в частности – реклама). 4) Пользователи-дети не влияют на решения взрослых об использовании нововведения. Рассмотрим домохозяйство, включающее трех взрослых (и произвольное число несовершеннолетних). Примером домохозяйства из трех взрослых людей (старше 18 лет) могут служить совместно проживающие жена, муж и совершеннолетняя дочь. Добавив свекровь, получим домохозяйство из четырех взрослых, добавив совершеннолетнего сына – из пяти. Упорядочим всех взрослых членов домохозяйств, включающих трех взрослых людей, по времени приобретения ими (или для них) личного мобильного телефона. Численность j-х взрослых членов домохозяйств, где проживает i взрослых, будем обозначать Xij. Так, например, X32 – это численность обладающих личными мобильными телефонами вторых взрослых членов домохозяйств, в которых проживает трое взрослых. 100% Доля взрослого населения России 80% u(t) 60% пользуются x(t) 40% владеют 20% Левада-центр: владельцы Левада-центр: есть в семье ФОМ: есть в семье Гфк-Русь: есть в д/х Модель: владельцы мар.12 сен.11 мар.11 сен.10 мар.10 сен.09 мар.09 сен.08 мар.08 сен.07 мар.07 сен.06 мар.06 сен.05 мар.05 сен.04 мар.04 сен.03 мар.03 сен.02 мар.02 сен.01 мар.01 сен.00 0% ФОМ: владельцы ВЦИОМ: есть в семье Ромир: пользователи ВЦИОМ: владеют лично Модель: пользователи Рис.1. Использование мобильной связи и владение сотовыми телефонами Соответствующие полные численности j-х в семейной очереди на покупку телефона взрослых, проживающих в домохозяйствах из i взрослых, обозначим Kij. Не все взрослые члены домохозяйств в момент t владеют сотовыми телефонами, поэтому их численность в каждом сегменте X (t ) K ij удовлетворяет ограничению ij . Поскольку Росстат публикует данные о домохозяйствах, численность взрослых в которых не превышает шести взрослых людей, условимся считать, что в домохозяйствах не бывает более шести взрослых. Таким образом, верхнюю границу J индексов i и j положим равной 6. Табл. 1 иллюстрирует выбранное разбиение. Суммирование всех элементов табл. 1 (численные значения элементов могут быть вычислены при помощи табл.2) дает полное число взрослых россиян K = 110 933 868 человек. Таблица 1. Сегментация взрослых россиян Первый Второй Третий взрослый взрослый взрослый Один взрослый K11 в домохозяйстве Двое взрослых K21 K22 4-й 5-й 6-й Трое взрослых K31 K32 K33 Четверо взрослых K41 K42 K43 K44 Пятеро взрослых K51 K52 K53 K54 K55 Шестеро взрослых K61 K62 K63 K64 K65 K66 Разделив численное значение каждого элемента таблицы на K, получим плотность распределения долей выделенных сегментов k ij K ij K . Таблица 2. Плотность распределения взрослых членов домохозяйств kij Первый Второй Третий 4-й 5-й 6-й Взрослы взрослый взрослый й Один взрослый 13,0% в домохозяйстве Двое взрослых 21,4% 21,4% Трое взрослых 9,0% 9,0% 9,0% Четверо взрослых 3,2% 3,2% 3,2% 3,2% Пятеро взрослых 0,6% 0,6% 0,6% 0,6% 0,6% Шестеро взрослых 0,2% 0,2% 0,2% 0,2% 0,2% 0,2% Сумма всех элементов табл. 2 равна единице. Суммируя элементы этой таблицы по столбцам, получаем доли первых, вторых и т.п. взрослых в домохозяйстве. Почти половина (47,5%) всех взрослых принадлежит к условной группе “глав семей”, и лишь у 18,1% взрослых очередность превышает “2”. Отметим, что последнее обстоятельство позволяет относительно успешно аппроксимировать данные опросов и без знания реального распределения домохозяйств по размеру [1]. Однако подход, используемый в [1] не позволяет моделировать ряд интересных данных, например, распределение ответов на вопрос ВЦИОМ о количестве пользователей сотовой связи в семье, распределение ответов на вопрос ФОМ о наличии телефонов у всех взрослых членов семьи и т.п. Модель, которая предлагается в настоящей работе, преодолевает указанное ограничение. Процесс приобретения первого мобильного телефона домохозяйством из i взрослых представим следующей моделью распространения инноваций, обобщающей модель Ф.Басса [2]: dX i1 U (t ) (t ) p q M i1 X i1 (t ) dt K (1) Здесь U(t) – суммарное число взрослых членов семей, в которых есть мобильные телефоны (в этой работе оно считается тождественным числу пользователей мобильной связи), σ(t) – сигма-функция, равная нулю при отрицательных значениях времени и единице при положительных. Модель содержит следующие неизвестные параметры: Mi1 – потенциал распространения нововведения в данной группе (число глав семей, которые рано или поздно начнут использовать сотовый телефон в домохозяйствах численностью i), q – параметр “внутреннего” воздействия или “имитации”, p – параметр “внешнего” воздействия (СМИ и рекламы). p 0, q 0 , Параметры модели удовлетворяют условиям: 0 M 1 j K1 j . В этой работе мы делаем упрощающее предположение о равенстве параметров p и q для всех групп. Кроме того, в этой модели предполагается, что для всех групп риск “заражения” идеей о необходимости приобретения мобильных телефонов пропорционален текущей доле пользователей сотовой связи в населении страны (а не, например, доле владельцев мобильных аппаратов, как предполагалось в работе [3]). Это предположение упрощает вычисления, но может оказаться неверным. Определим параметры i : i M i1 M где M – потенциал распространения сотовых телефонов среди всего населения России. (Величина M нам заранее неизвестна и должна быть оценена в ходе моделирования данных опросов. Очевидно ограничение: M K ). Предположим далее, что потенциалы распространения мобильных телефонов среди глав домохозяйств пропорциональны численности таких домохозяйств: i k i1 (2) Иными словами, распространение нововведения среди глав домохозяйств не зависит от численности домохозяйств. Сделанное предположение позволяет существенно сократить число неизвестных: вместо шести потенциалов Mi1 теперь необходимо определить только один M. В реальности, как свидетельствует опыт скандинавских стран, крупные семьи осваивают новинки ИКТ раньше, а позже всех нововведения начинают использовать одинокие люди. Однако в нашем распоряжении нет необходимых для изучения этого явления российских данных. Предположение (2) позволяет получить совершенно идентичные выражения для долей (не численностей!) пользователей сотовой связи и домохозяйств, в которых имеются мобильные телефоны. Равенство этих долей подтверждается данными опросов (рис.1) и именно оно позволяет использовать данные опросов о наличии сотового телефона в семье и об использовании сотовой связи как идентичные. Если отказаться от предположения (2), то эти два вида данных потребуется моделировать отдельно. J i k1 i 1 Сумма есть отношение числа семей (домохозяйств) к численности взрослых граждан. В России параметр α составляет 0,475, что проверяется суммированием элементов второго столбца табл. 2. В силу определения элементов таблицы 2 J i i 1 i1 i k i1 1 . Чтобы получить численность домохозяйств, использующих сотовую связь, просуммируем уравнения распространения нововведений для глав семей различной численности: J dX i1 U (t ) J ( t ) p q M i1 X i1 (t ) K i 1 i 1 dt i 1 J Учитывая, что J J J i 1 i 1 i 1 M i1 i M M 1 M . получаем U (t ) dV (t ) p q M V dt K (3) J V (t ) X i1 i 1 где – численность домохозяйств, в которых есть сотовый телефон. Несложно показать, что при условии одновременного начала распространения нововведения в семьях разного размера решения для глав домохозяйств, где проживает i взрослых, имеют простой вид: X i1 (t ) i V (t ) Совокупное число взрослых в домохозяйствах, где есть хотя бы один сотовый телефон: J W (t ) iX i1 (t ) i i 1 J i 1 1 V (t ) V (t ) i i V (t ) i 1 . члены Поскольку мы предполагаем, что все взрослые семьи одновременно начинают использовать сотовую связь: U (t ) W (t ) , следовательно уравнение (3) превращается в уравнение модели Ф.Басса: V (t ) dV (t ) p q M V dt K (4) Деля обе стороны (4) на α, получаем такое же уравнение для численности пользователей: U (t ) dU (t ) p q M U dt K (5) Наконец, для “глав” домохозяйств получаем чрезвычайно простое выражение: X i1 (t ) iU (t ) (6) Предположим, что домохозяйства постепенно приобретают сотовые телефоны, не только для “глав”, но и для других взрослых (хотя необязательно – для всех) с некоторой, распределенной во времени, задержкой, которую может быть вызвана, например, ограниченным бюджетом. Тогда численность обладающих личными мобильными телефонами j-х взрослых членов домохозяйств, где проживает i взрослых, можно описать сверткой: X ij (t ) g ij (t ) X i1(t ) Если выбрать функции распределения задержек в виде δ-импульсов, g ij (t ) ij (t ij ) по времени задержки ij ( , то покупка сотового телефона для j-го члена семьи отстает от покупки телефона для главы семьи на время ij 0 ): X ij (t ) ij X i1(t ij ) 0 1 ij , где . В настоящей работе мы используем простую модель: X ij (t ) j 2 X i1 t ( j 1) (7) при j i 2 , и с ограничениями на параметры: 0 1 , 0 1 . Таблица 4. Коэффициенты модели (7) Первый Второй 3-й 4-й взрослый взрослый 5-й 6-й 1 Один взрослый в домохозяйстве 2 2 Двое взрослых 3 3 3 Трое взрослых 4 4 4 Четверо взрослых 4 2 5 5 5 Пятеро взрослых 5 2 5 3 6 6 6 Шестеро взрослых 6 2 6 3 6 4 В этой модели задержка пропорциональна порядковому номеру взрослого члена домохозяйства, при этом телефоны необязательно приобретаются для всех взрослых. В частности, при 0 телефонами владеют только главы семей, а при 0 - только первый и второй члены семьи. При наличии дополнительных данных можно попробовать связать задержки с социально-демографическими переменными, такими как возраст, статус, профессия членов домохозяйств (молодежь, руководители, занятые в сфере ИКТ могут приобретать телефоны раньше). Используя равенство (6), получим: X ij (t ) i j 2U t ( j 1) Полное число владельцев сотовых телефонов в момент времени t: J i X (t ) X ij (t ) V (t ) i i, j i 2 j 2 U t ( j 1) . j 2 Меняя порядок суммирования, окончательно получаем: J X (t ) U (t ) jU t ( j 1) j 2 , (8) J о j 2 i i j где . Такое число взрослых людей на вопрос “Есть ли у Вас лично мобильный сотовый телефон?” может искренне дать утвердительный ответ. Наилучшим образом (в предположении логнормального распределения ошибок) данным опросов удовлетворяют параметры модели, указанные в табл.5. Таблица 5. Параметры оптимальной модели M/K q(год-1) p (год-1) τ (год) 85,84% 0,8 1,77·10-5 1,09 β 1,0 Γ 1,0 Результаты расчетов доли взрослых владельцев сотовых телефонов доли взрослых пользователей U (t ) / K и доли домохозяйств, использующих мобильную связь V (t ) / K , изображены на рис. 1, вместе с данными социологических опросов. Как иллюстрирует рис. 1, модель удовлетворительно объясняет результаты опросов, проведенных пятью организациями: ФОМ, ВЦИОМ, Левада-центра, Ромир и Gfk. X (t ) / K , Список литературы: 1. Делицын, Л.Л. Совместное использование различных единиц отбора данных при моделировании распространения инноваций /Тезисы доклада на II Всероссийской научно-практической Интернет-конфереции “Информационные системы и технологии в социально-экономических и правовых процессах [Электронный ресурс]/ – Электрон. текстовые дан. – Режим доступа: http://www.sksi.ru/sections_main/conferences/conferences/2_nauchno_prakt_i_net _konf/articles/3/delitsin.doc. – Загл. с экрана. 2. Bass, F. M. A new product growth for model consumer durables // Management Science. – 1969. - Vol. 15. - pp. 215–227. 3. Юрина, Э.А., Делицын, Л.Л. “Эпидемиологические" модели распространения мобильной связи и Интернета в России / Интернетмаркетинг. – 2008. - №1 (43). – С.2-15. Резюме Построена модель распространения инноваций, объясняющая результаты опросов о личном владении новинкой, об ее использовании и о наличии ее в семье. Использованы данные Переписи населения 2002 г. о размерах домохозяйств. Определены параметры модели, наиболее близко аппроксимирующей результаты опросов, проведенных пятью организациями. Summary The model of distribution of innovations explaining results of interrogations about personal possession of a novelty, about its use and about presence it in family is constructed. Are used given account of the population of 2002 about the sizes possession. The parameters of model are determined, is closest averaging results of the interrogations which have been carried out by five organizations.