Документ 3642778

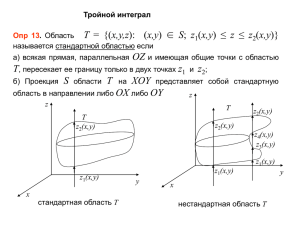
Лекция 7
Формула Гаусса-Остроградского
Формула Гаусса-Остроградского является одной из наиболее важных формул в
векторном анализе. Она связывает поток векторного поля через замкнутую поверхность с
напряженностью векторного поля внутри замкнутой поверхности. Для векотрного поля

F  P; Q; R  :

 F d

s 
Sвнеш
 P
  x

V
Q
R 
dxdydz ,

y
z 

причем поверхностный интеграл потока векторного поля берется по поверхности через
внешнюю сторону (вектор нормали к поверхности направлен «наружу»). Правую часть
формулы можно переписать в виде:


 P Q R 




dxdydz

div
F
dxdydz


F
dxdydz ,



 x y z 

V 
V
V
где

P Q R
     
– дивергенция векторного поля F ,   ex  e y  ez – оператор
 
x y z
x
y
z
Гамильтона (набла).
Формула Гаусса-Остроградского справедлива, если выполняются два условия. Вопервых, поверхность S должна быть кусочно-гладкой, т.е. такой, что в любой ее точке
можно провести касательную плоскость (поверхность задается дифференцируемыми
функциями) и двусторонней (направление нормали при движении вдоль поверхности


div F   F 

сохраняется. Во-вторых, векторное поле F  P; Q; R  должно быть таким, что функции
P  Px, y, z , Q  Qx, y, z , R  Rx, y, z  и их частные производные по x, y и z непрерывны в
области V.
Другие варианты формулы Гаусса-Остроградского.

Запишем выражение для вектора нормали: n  cos ; cos  ; cos   , где  ,  ,  – углы,
которые вектор нормали составляет с осями координат.
z


γ 
d
s

n ds .
y
n

β
Отсюда  P cos   Q cos   R cos  ds   div Fdxdydz
α
x
S
V
Кроме
того,
имеет
место
следующая
формула:

 Pdydz  Qdzdx  Rdxdy    div Fdxdydz
S
V
Доказательство формулы (1 вариант):
 
 ( F  n
Sвнеш
в неш
)d s 
 P
  x 
V



Q R 
dxdydz Представим векторное поле в виде суммы

y
z 




векторных полей: F  F 1  F 2  F 3 , где F 1  0,0, R , F 2  0, Q,0, F 3  P,0,0 , найдем
потоки этих векторных полей по отдельности, а затем сложим их.

Рассмотрим сначала случай поля F 1 . Замкнутая поверхность является цилиндроидом,
ограниченным сверху и снизу поверхностями, заданными в явном виде: z  z1 x, y  (снизу) и
z
z  z2 x, y  (сверху). Поверхность S состоит из
нижней S1, боковой S2 и верхней S3 поверхностей.
Рассмотрим поверхностный интеграл по S1. D –
проекция S1 на плоскость xy.
S3
z=z2(x,y)
S2
y
S1
z=z1(x,y)
D
Координаты
 z1 z1


 x ; y ;1



x

n
вектора
 z1
 z 
1  1   
 y
 x 

2
нормали:
.




2
Так как вектор нормали направлен вниз (координата по z отрицательна), то в формуле




R x, y, z1  x, y 
для n нужно выбрать знак «+». F 1  n  0,0, R   n  
.
 z   z 
1   1    1 
 x   y 
2
2
 z 
 z 
1   1    1   dxdy
 x 
 y 
2
Дифференциал
поверхности
ds 
равен:
R x, y, z1  x, y 
2
Отсюда
2
 z   z 
 1   1    1   dxdy    R x, y, z1  x, y dxdy
S ( F1  n )d s  D 
2
2
 x   y 
D
1
 z1   z1 

1 
  
 x   y 
 
2

Интеграл по боковой поверхности S2. Вектор нормали n  n1 ; n2 ;0 , так
 

как нормаль параллельна плоскости xy. F1  n  0;0; R   n  0 . Какая бы ни
D
была боковая поверхность, интеграл по ней равен нулю:
 
 ( F1  n )d s  0
S2
Интеграл по поверхности S3Рассматривается аналогично интегралу по
поверхности S1 с той разницей, что вектор нормали направлен в
 z 2 z 2 
 
;
;1
y 
 x

противоположную сторону – вверх: n 
 z   z 
1   2    2 
 x   y 
2
произведение

F1
на вектор нормали:


F 1 n 
. Скалярное
2
R x, y, z 2  x, y 
 z   z 
1   2    2 
 x   y 
2
2
 z   z 
дифференциал поверхности: ds  1   2    2   dxdy
 x   y 
2
2
,
 
 ( F  n )d s   Rx, y, z x, y dxdy
1
1
S3
D
Сложим интегралы по поверхностям S1, S2 и S3:
  
  
  
  








F

n
ds

F

n
ds

F

n
ds





 1 
 1 
 1 
 F1  n ds    Rx, y, z1 x, y dxdy   Rx, y, z 2 x, y dxdy 
S внеш
S1
S2
S3
D
D








  ( Rx, y, z 2 x, y   Rx, y, z1 x, y )dxdy
D
Рассмотрим тройной интеграл по объему V:
z2 ( x , y )
R
R
dxdydz   dxdy 
 dz   Rx, y, z  zz  zz12((xx,,yy)) dxdy   ( Rx, y, z 2 x, y   Rx, y, z1 x, y )dxdy


z

z
V
D
z1 ( x , y )
D
D



Таким образом, для векторного поля F 1  0,0, R  формула Гаусса-Остроградского


 F1  d s 
Sвнеш
R
 z dxdydz доказана.
V

Аналогично доказывается формула, если взять поле F 2 , и в качестве замкнутой

поверхности взять цилиндроид, ось которого направлена вдоль оси y. F 2  0, Q,0

Q

 F  d s   y dxdydz (доказывается аналогично)
2
Sвнеш
V

Аналогично и для поля F 3  P,0,0 :

P

 F  d s   y dxdydz
3
Sвнеш



V

Если взять поле F  F 1  F 2  F 3 , то

 P

 F d s    x 
Sвнеш
V
Q R 
dxdydz – формула

y
z 
Гаусса-Остроградского в общем виде верна.
При доказательстве мы использовали замкнутую поверхность, которая может быть
представлена как цилиндроид с осью, направленной вдоль осей x,
y или z. Такой
поверхностью является прямоугольный параллелепипед. Если
рассмотреть произвольную поверхность, то справедливость
формулы не очевидна.
Разобьем произвольную поверхность на две – S1 и S2.
Проинтегрируем векторное поле по каждой
поверхности и сложим. Получатся интегралы
по S1, S2 и два интеграла по сечению.
Интегралы по сечению отличаются только знаком (так как векторы
нормалей направлены в разные стороны), они уничтожаются при
сложении. Поэтому поверхность можно разбивать на части, интегрировать по ним,
результаты складывать.
Произведем сечение замкнутой поверхности большим
числом перпендикулярных плоскостей. Формула ГауссаОстроградского будет верна всюду, кроме границ
поверхности, на границах становится справедливой при
устремлении диаметра разбиения к нулю. Отсюда следует, что формула ГауссаОстроградского справедлива для любой кусочно-гладкой поверхности.
Пример.



В качестве поля F возьмем радиус-вектор: F  r  x, y, z , S – сфера радиуса R с центром
в начале координат.
Для нахождения потока вектора воспользуемся формулой Гаусса-Остроградского:



3
 r d s   div r dxdydz   3dxdydz  3V  3Vсферы  4R
Sвнеш
V
V
Формула Ньютона-Лейбница представляет интеграл по отрезку по значениям
первообразной на границах отрезка. Формула Гаусса-Остроградского представляет собой,
по существу, то же самое (вместо отрезка – объем, вместо границ отрезка – замкнутая
поверхность). Эту формулу, как и формулу Грина, можно считать обобщением формулы
Ньютона-Лейбница.