Лекция № 10.

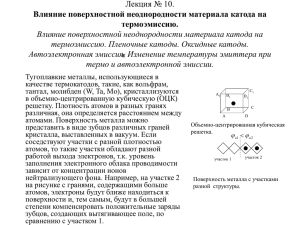
Лекция № 10.
Влияние поверхностной неоднородности материала катода на термоэмиссию.
Пленочные
катоды.
Оксидные
катоды.
Автоэлектронная
эмиссия.
Изменение
температуры эмиттера при термо и автоэлектронной эмиссии.
§ 9.7. Влияние поверхностной неоднородности материала катода на термоэмиссию.
Тугоплавкие металлы, использующиеся в качестве термокатодов, такие, как вольфрам,
тантал, молибден (W, Ta, Mo), кристаллизуются в объемно-центрированную кубическую
(ОЦК) решетку.
Плотность
B1
C1
А1
атомов
определяется
в
разных
расстоянием
между
D1
E
расстояние между точками AE 
C
B
А
a
D
Рис.9.13. Объемноцентрированная
кубическая решетка.
гранях
различная,
атомами.
она
Например,
a2 a2 a 3


меньше,
2
4
2
чем между AD = a (рис.9.13). Следовательно, плотность
атомов в плоскости грани АА1С1С больше, чем в плоскости
AA1D1D.
Поверхность металла можно представить в виде зубцов
различных граней кристалла, выставленных в вакуум. Если
соседствуют участки с разной плотностью атомов, то такие
участки обладают разной работой выхода электронов, т.к.
участок 1
участок 2
 a1   a 2
уровень заполнения электронного облака проводимости
зависит от концентрации ионов нейтрализующего фона.
Например, на участке 2 (рис.9.14) с гранями, содержащими
Рис.9.14. Поверхность
металла с участками
разной структуры.
больше атомов, электроны будут ближе находиться к
поверхности и, тем самым, будут в большей степени
компенсировать положительные заряды зубцов, создающих вытягивающее поле, по
сравнению с участком 1. Другими словами, можно сказать, что электроны легче
удерживаются в плоскости граней, содержащих большую концентрацию атомов, т.е. на
участке 2 работа выхода электронов будет больше, чем на участке 1. Тогда на поверхность
даже чистого металла можно рассматривать как пятнистую с областями, обладающими
различной работой выхода.
Между

EП
 min  max
 min
этими
областями
возникает
контактная
разность потенциалов, создающая над незаряженной
металлической поверхностью электрическое поле. Это

поле можно назвать полем пятен E П (рис.9.15). Оно
 max
направлено
таким
образом,
чтобы
сдерживать
электроны, эмитированные пятнами с малой работой
Рис.9.15. Участки поверхности с
разными работами выхода.
выхода и ускорять электроны на участках с большой
работой выхода.
Т.о. коллективное действие плазмы металла стремится нивелировать возникающие
неоднородности.
eU  WF  e a 
При
этом
изменяется
потенциальная
энергия:
e2
 eEx  eE П x П . Эмиссия прежде всего идет с областей с  min , так
4x

потенциальный барьер понижен на величину U   E П dx (рис.9.16). Среднее значение 
0
определяем
 
из
соотношения:
kT  Smin
 e
ln 
exp   min
e  S
 kT
 e 
I  I max  I min  S  A  T 2  exp  
,
 kT 
 e
  Smax
exp   max
 
S

 kT

 . Надо учесть, что

тогда
x П  x (область
действия поля пятен меньше области действия внешнего электрического поля). На
больших расстояниях внешнее электрическое поле возьмет свое и «загнет» ход кривой
xкр
потенциальной энергии. Поэтому максимум все равно будет, причем: U 1 
 E
П
 E dx ,
0
где положение максимума определяется из соотношения E П x кр   E . При дальнейшем
увеличении E U1 падает, и термоэмиссионный ток резко возрастает.
Этот эффект получил название аномального
e
эффекта Шотки. Это аномальное увеличение тока
прекратится, как только U1  0, т.е. E П  E .
U
U1
E  EП
 eE x
 eE x
E  E G
WF
Рис.9.16.
Потенциальная
диаграмма для пятен с  min .
дальнейшем
увеличении
E
эмиссия
с
областей, имеющих  min , будет происходить
x
x кр
При
независимо от пятен с  max , увеличение тока
термоэмиссии будет соответствовать снижению
работы выхода по нормальному эффекту Шотки:
e aE   e min
 e3 / 2 E1/ 2 .
Поле
пятен
понизит
барьер для пятен с  max (рис.9.17), но в случае
E  E П пятна с  max так же перестанут замечать
 eE П x П
e
поле пятен E П , и увеличение термотока будет
соответствовать нормальному эффекту Шотки во
E0
внешнем
 eEx
e aE   e max
E  EП
WF
электрическом
 e 3 / 2 E 1 / 2 . По экспериментальной
зависимости ln j
Рис.9.17.
Потенциальная
диаграмма для пятен с  max .
поле:
 E  можно определить порядок
электрических полей пятен E П , а скачок ln j 
имеет
порядок
разности
   max   min : ln j  
ln j
EП 
участок аномального
эффекта Шоттки

y
работ
выхода
e
. Учитывая, что
kT
, можно оценить характерный размер
пятен. Следует иметь ввиду, что наличие пятен с
E
EП
разной работой выхода деформирует прямую
Ричардсона зависимости ln
jT
1
 f   (рис.9.10),
2
T
T 
т.к. при низких температурах эмиссия идет в
Рис.9.18.
Зависимость
термоэлектронного
тока
от
напряженности электрического поля.
основном с областей с
 min , при высоких
подключаются области с  max .
§ 9.8. Пленочные катоды.
В 1913 г. Ленгмюр обнаружил, что вольфрамовый катод с примесью окислов тория
ThO2 (0,5-1,5%) после соответствующей термической обработки дает эмиссионные токи
на несколько порядков больше, чем чистый вольфрам. Термическая обработка происходит
в три этапа:
1. T  2600K (t ~ 15 мин) : ThO 2  Th  O 2 ;
2. T  2600  2300 K : диффузия Th к поверхности ;
3. T  1800 K : прекращение диффузии Th ;
Атомы
тория
находятся
на
поверхности W в виде диполей, т.к.
- +
W
работа выхода для тория меньше, чем
Th
для W. В результате работа выхода для
- +
W+Th
- +
понижается
чистым W:
по
сравнению
с
  W  W Th  4nd pd ,
где n d - число диполей на 1 см2, а p d дипольный момент.
Пусть
eV
e
eW
x
+
e
x
+
Рис.9.19.
Потенциальная
пленочного катода.
диаграмма
монослоя,
 e 
При   1 j  j1  A1T 2 exp   1 
 kT 
 e 
j  j  A T 2 exp    
 kT 
e
j 
ln  W2   ln AW  W ;
kT
T 
e
e max
 j 
ln  12   ln A1  W 
;
kT
kT
T 
С образованием
«холма»
-
плотность
nd
- степень покрытия.
n1
При 
eV
eW
-
 e 
При   0 j  j w  AW T 2 exp   W 
 kT 
Без образования
«холма»
-

n1
для
e
e max
 j 
ln  2   ln A  W 
.
kT
kT
T 
Полагая ln Aw  ln A1  ln A , найдем
 j 
j
jW
ln   

ln
2
T 2   jW  .
 T
j
j


ln 12  ln W2 ln  j1 


T
T
 jW 
ln
степень
покрытия:
Так
экспериментально
по
термоэмиссионному току можно определять степень покрытия. Степень покрытия зависит
от двух конкурирующих процессов диффузии тория к поверхности и испарения с
поверхности. Можно определить оптимальную степень покрытия. Диффузионный ток
пропорционален,
согласно
закону
Гука,
градиенту:
J   Dn   DnS  n0   Dn0  nS   Dn 0 ( n0 n S ), где n 0 - плотность в объеме,
nS -
ln I
плотность
на
поверхности.
 dnS 
 Ed 
 dt   D0 n0 exp   kT  ,

D


ln I W

Рис.9.20. Зависимость
степени покрытия.
что
график
E
 dn 
ln  S   ln( D0 n0 )  d будет
kT
 dt  D
зависимости
  0.7
так
Т.е.
являться «прямой диффузии» (рис.9.21). Скорость
тока
от
уменьшения
атомов
тория
на
поверхности
определяется теплотой испарения LTh , так что:
 dn S 
 L 

  B0 exp   Th  ,
 dt V
 kT 
B0  const ,
где
следовательно,
график
зависимости
L
 dn 
ln  S   ln( B0 )  Th , будет являться «прямой испарения» (рис.9.21). Пересечение
kT
 dt V
 dn 
ln  s 
 dt 
прямой диффузии и прямой испарения
определяет равновесную температуру. Для
Прямые испарения
3
Прямая диффузии
2
температуры
существует
своя
равновесная концентрация, когда прямая
испарения
будет
пересекать
прямую
диффузии именно в этой точке, так что
1
1
T1
каждой
1
T2
1
T3
1
T
Рис.9.21.
Зависимость
равновесной
концентрации от температуры.
 dnS 
 dn 

  S  ,
 dt V  dt  P
т.е.
nS  const .
И
наоборот, для каждой степени покрытия
существует своя равновесная температура,
которую можно определить как координату точки пересечения прямых (рис.9.21).
Пленочные катоды могут быть получены нанесением пленок на поверхность извне.
Щелочные металлы легко отдают свои валентные электроны на обобществление в
металле. Если поверхность вольфрама контактирует с парами цезия или бария, то
поверхность покроется атомами щелочного металла. Так как работа выхода щелочного
металла (для цезия eaCs  1.9 эВ, для бария eaBa  2.5 эВ)существенно меньше работы
выхода вольфрама ( eW  4.5 эВ), поэтому катоды W-Cs и W-Ba будут давать существенно
больший термоток, чем чистый вольфрам.
§ 9.8. Оксидные катоды.
Оксидный катод чаще всего применяется в бытовой технике, осциллографах,
кинескопах, СВЧ лампах благодаря малой работе выхода (1.2 эВ). Высокая эмиссионная
способность окислов BaO, CrO, CaO была открыта еще в 1904 г. Долгое время это не
находило объяснения. Квантовая теория металла стала складываться только в 1928-1930
гг. В настоящее время оксидный катод (ОК) – это слой смеси BaO+SrO, нанесенный на
металл, причем это слой ~1 мкм, а не одноатомная пленка, причем слой этот является
полупроводником. После прокаливания на поверхности солей
Sr++
O--
карбоната и стронция соли разлагаются, оставляя
Пустой кислородный узел
оксиды на поверхности: BaCO3 = CO2 + BaO,
Ba
SrCO3=CO2+SrO. Получающиеся таким образом
+
Ba
оксидные катоды не активированы. Оксидное
покрытие
не активированный
активированный
является
диэлектриком,
поэтому
обладает плохими термоэмиссионными
Зона
проводимости
свойствами.
Это
покрытие
активировать.
Процесс
активации
необходимо
состоит
в
нагревании до температуры порядка 1200 К. В
Примесные
уровни Ba
результате кислород уходит из покрытия, а часть
молекул
Заполненная
зона
окиси
бария
восстанавливается
до
металлического бария, атомы которого находятся
внутри кристаллов окислов. Появление в слое
Рис.9.22. Превращение диэлектрика в
примесный полупроводник.
свободного бария сопровождается образованием в
решетке BaO пустых кислородных узлов, вблизи которого возможно закрепление
электрона на примесном уровне, лежащем чуть ниже зона проводимости (рис.9.22). При
нагреве электроны с этих примесных уровней переходят в зону проводимости, затем из
зоны проводимости в вакуум. Для перехода электрона
с примесного уровня в зону
проводимости требуется всего 0.2 эВ, что значительно меньше ширины запрещенной зоны
(для BaO порядка 4 эВ), которую нужно преодолеть электронам из заполненной зоны.
Ширина зоны проводимости оксида бария (потенциальный барьер для перехода электрона
в вакуум) составляет примерно 1 эВ, поэтому работа выхода порядка 1.2 эВ. Хотя пустые
кислородные узлы при активации образуются около поверхности, но ионы кислорода из
толщи
покрытия
перемещаются
в
эти
свободные
узлы,
так
что
происходит
распространение примесных атомов бария по всему слою оксида. Концентрация
электронов, перешедших в зону проводимости с примесных уровней, мала, поэтому они
не вырождены. Вывод формулы Ричардсона был сделан самим Ричардсоном для не
вырожденных электронов, поэтому плотность тока по прежнему определяется формулой:
A
 e 
, где ea  1.2 эВ.
j  AT 2 exp   a  , A  120 2
см град 2
 kT 
X. АВТОЭЛЕКТРОННАЯ ЭМИССИЯ.
§ 10.1. Прозрачность барьера.
Автоэлектронная эмиссия – это явление эмиссии электронов при низкой температуре в
присутствии внешнего электрического поля. В присутствии внешнего электрического
поля высокой напряженности E (106107 В/см), помимо увеличения тока эмиссии за счет
снижения работы выхода (эффекта Шоттки), из-за ограниченности толщины барьера
появляется вероятность подбарьерного перехода – «тунельного» эффекта. Испускание
электронов под действием внешнего электрического поля, обусловленное вероятностью
подбарьерного перехода потенциального барьера, имеющего во внешнем электрическом
поле ограниченную ширину, называется автоэлектронной эмиссией.
Если
на
поверхность
раздела
двух
электромагнитная волна с энергией W x
Wx
падает
(рис.10.1), то
происходит ее отражение от потенциального барьера.
W
1
сред
Однако на некоторую глубину она все-таки проникает,
2
затухание волны характеризуется волновой функцией, так в
x
0
Рис.10.1. Граница раздела
двух сред.
вектор.
Вероятность
 4
 h
 2  a 22 exp  
2
среде 2 она будет иметь вид:  2  a2 exp ik 2 x   a2 e  kx , где
k2 
2
h
2m(W x  W )  ki , k 
нахождения
2
h
электрона
2m(W  W x ) - волновой
в
точке
x:

2m(W  W x ) x  . Т.о. для бесконечного вдоль x потенциального

барьера все электроны в конце концов отразятся от барьера.
Рассмотрим теперь потенциальный барьер конечной
ширины.
Wx
d
1
2
Тогда
существует
вероятность
нахождения электрона в среде 3 (рис.10.2). Относительная
плотность
3
электронов
среде
3
определяется
коэффициент прозрачности барьера для прямоугольного
барьера ширины d:
вычисления
 4

D  exp  
d 2m(W  W x )  . Для
 h

прозрачности
потенциального
барьера
непрямоугольной формы можно его разделить на ряд
x2
dx
в
вероятностью нахождения электрона на расстоянии d , т.е.
x
x1
ненулевая
прямоугольных барьеров ширины dx, и проинтегрировать
Рис.10.2. Потенциальный
барьер конечной ширины.
по ширине барьера (рис.10.2):
 4
D  D1D2 ...Dk  exp  
 h

x2

x1

 2 x2

2m(W  Wx )dx   exp    2m(W  Wx )dx  .



x1



Рассмотрим
туннельный эффект для электронной эмиссии. На рис. 10.2. изображена форма
Потенциального барьера на границе
металл
4
x
3
Wa
Wx
присутствии
внешнего электрического поля.
Зона
 eE x
x1
x2
Рис .10.3. Потенциальный барьер на границе
металл – вакуум в присутствии внешнего
электрического поля
Вычислим
в
«чистая» автоэлектронная эмиссия.
2
1
a
вакуум
Зона 1 в распределении электронов –
e
EF
–
прозрачность
треугольного
2
–
автотермоэлектронная
эмиссия.
Зона 3 – термоэлектронная эмиссия,
вызванная эффектом Шоттки.
Зона 4 – термоэлектронная эмиссия.
барьера
(без
учета
сил
электрического
изображения). Заменим реальную форму барьера на треугольную (рис. 10.4).
В
eV
e a
0
x
x2
 eE x
Wa
Коэффициент
прозрачности
граница интегрирования x1  0 , а верхняя определяется
0
2m(eEx  Wx )dx  

Wx  eEx2 , x2  
Wx
.
eE
Введем
интеграл:
2m
Wx
0
равенства:
обозначения:  eEx  Wx   , d  eEdx . Вычислим
Рис.10.4. Потенциальный
барьер на границе металл –
вакуум в присутствии внешнего
электрического поля без учета
сил электрического
изображения.

потенциала
eV x  eEx, x  0 .
из
Wx  0
Wx
eE
распределение
 2 x2

барьера D  exp    2m(eV x   Wx )dx  , где нижняя
 hx

1


Wx
EF

вакууме
d
2m

eE
eE
0

 d 
Wx
2m
eE
Wx

 d 
0
2 2 m
(Wx ) 3 2 ;
3eE
 4 2m

(W x ) 3 2  .
тогда: D  exp  
 3 eE

Вычислим прозрачность потенциального барьера с учетом сил электрического
изображения (рис. 10.5). В вакууме распределение потенциала eV x   eEx 
eV
0
e a
e
2
3
Точки x1 и x 2 находим из равенства Wx  eEx 
E
x
e2
4x
Wx
получим уравнение eEx 2  Wx x 
 eE x
EF
Wa
Wx  Wx (1 
x1 
x1
e2
, x  0.
4x
2eE
x2
Рис.10.5. Потенциальный
барьер на границе металл –
вакуум в присутствии внешнего
электрического поля с учетом
сил электрического
изображения.
e3 E 3 2
)
Wx2
.
e2
,
4x
e2
 0, корни которого
4
Учтем,
что
снижение
потенциального барьера за счет эффекта Шоттки
  ea   e
3
2
E много меньше энергии Wx , то есть
e3 E  (ea ) 2  Wx2 при a  a , тогда в разложении
(1 
e3 E 3 2
1 e3 E
)

1

 ...
Wx2
2 Wx2
Wx  Wx 
x1 
1 e3 E
2 Wx
2eE
возьмем
1 e2

, x2 
4 Wx
Wx  Wx 
только
1 e3 E
2 Wx
2eE
первые
два
слагаемые:
Wx 1 e 2


.
eE 4 Wx
Для этих пределов интегрирования вычислим интеграл:
x2

 eEx  W x 
x1
1 e

2 E

x2

x1
e2
dx 
4x
x2

x1
1
1 1 32
1 e
 W x  e 3 2 E 
e
E
d 
2
2
2 E
1
1
1
1 e
 W x  e 3 2 E  e 3 2
E d 
 Wx
2
2

2 E
2
32
3
1 e
1e
E
1
1 y
 Wx  2
 Wx  1 
(  ) d 
2 E
2 Wx

2 eE
1
Были
 y 
введены
3
y
4
2 y

y 2

y
2
1
следующие
y
1
(  )d
2

обозначения:
x2
1 e3 2 E 1 1 e3 2 E
1 

d 
2
Wx
2  Wx

x1
2 y

y 2

1
y
2
y
1
(  ) d .
2

1
e
e3/ 2 E
x 
,y
.
2
E
Wx
называется
функцией
Выражение
Нордгейма,
тогда
 4 2m

D  exp  
  y (W x ) 3 2  .
 3 eE

§ 10.2. Плотность тока автоэлектронной эмиссии.
Число электронов, падающих на единицу поверхности в единицу времени и имеющих

 p x2


 EF
4mkT  p x2  
  2m


d
ln
1

exp
импульс от p x до p x  dp x :  x  V x dn x 
 2m  

kT
h3

 





 .




Плотность тока автоэлектронной эмиссии:
j A   eD x . Обозначим
0

p x2
 E F  E x  E F , тогда:
2m


4mkT
 E  EF
jA 
dE x D ln 1  exp   x
3

kT
h


0


  4mkT
  
D ln 1  exp  
  
 d .
3

h
 kT  


0
p x2
 Ex ,
2m
При   0 ток автоэлектронной эмиссии обусловлен только электронами, лежащими
ниже уровня Ферми, т.е. будет существовать и при T  0 . Примем при   0 :


  
.
ln 1  exp  
   
kT
 kT  

Обозначим
4 mkTe

4 me
D( )d    3  D d  («чистая» автоэлектронная эмиссия).
3

h
kT
h 

0
jAЭ 
  0:
для
0
Wx  E x  Wa  E x  E F  E F  Wa  e a   .
Относительно
переменной
 можно
 4 2m
3 
  y e a    2  . Можно разложить эту
выразить прозрачность барьера: D  exp  
 3 eE

 4 2m

3
  y e a  2  A  ...  D0 exp  A  ,
функцию по малому параметру  : D  exp  
 3 eE

 4 2m
3 
  y e a  2  - прозрачность барьера для электронов на уровне
где D0  exp  
 3 eE

Ферми,
j

AЭ
A
коэффициент
0
4 me
D  exp  A  d  .
0
h3

0
1
exp  A d  A exp  A 
jAЭ
2 2m
e a  12   y a    2 2m e a  12 .
eE
eE
Тогда:
Интеграл
0
0

1
1
  exp  A d   2 . Тогда:
A 
A
 C  e  3 2
 4 2m
3 
e3 E 2
a
2
2

exp  
  y  ea    C1E exp   2
8 h  ea 
3
eE

E




 - формула Фоулера

Нордгейма. Коэффициенты C1 и C2 можно определить экспериментально, для этого
необходимо
построить
зависимость
C e a 
j 
ln  AÝ2   C1  2
E
E 
3
Нордгейма можно представить как функцию переменной  
2
1
 f  .
E
ш
a
Функцию
ш
e3/ 2 E1/ 2


.
Wa  Wx Wa  Wx
Некоторые значения функции Нордгейма () представлены в таблице 10.1.
Таблица 10.1.
ш/ a
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0

1
0.98
0.94
0.87
0.79
0.69
0.58
0.45
0.31
0.16
0
Для 0 <  < 1
()  0.955 – 1.03 2. Тогда плотность тока автоэлектронной эмиссии
можно описать формулой:
(e a ) 3 / 2  ( ш /  a )
А
E2
j АЭ [ 2 ]  B0 
 exp( 
)
e a
E / E0
см
 6.2  10  6 
E F / e a E 2 [ В / см]
E F  e a
 exp( 
6.85  10 7  (e a ) 3 / 2  ( ш /  a )
),
E[ В / см]
где EF – энергия Ферми, B0=e2/(8h), E0=8 2me /(3he). Влияние множителя E2, подобно
влиянию множителя
T2
в формуле Ричардсона-Дэшмана, незначительно. Более
существенно влияние экспоненциальной зависимости от работы выхода электрона ea.
Автоэлектронная эмиссия становится заметной при E ~ 106
В
. Если на поверхности
см
катода есть острия с радиусом порядка микрометра, именно автоэлектронная эмиссия с
микроскопических
промежутков.
острий
чаще
Автоэлектронные
всего
катоды
является
специально
причиной
пробоя
изготовляются
в
вакуумных
виде
игл
(«острийный катод»). Преимущество автоэлектронной эмиссии состоит в том, что при
эмиссии катод не охлаждается, а наоборот, нагревается, т.к. эмитируются электроны с
энергией E x  E E без потерь энергии, и их место занимают электроны с более высоких
уровней, они то и разогревают катод.