Неравномерное движение в вертикальной плоскости
реклама

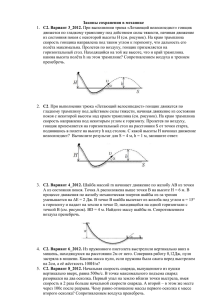
1. Система из грузов m и M и связывающей их лёгкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей через центр закреплённой сферы. Груз m находится в точке А на вершине сферы (см. рисунок). В ходе возникшего движения груз m отрывается от поверхности сферы, пройдя по ней дугу 30°. Найдите массу М, если m = 100 г. Размеры груза m ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы. m M 3 3 2 m 3 cos 2 2 M 100 г 330 г. π 3 cos 3 3 2 2. Наклонная плоскость AB длиной 1 м и горизонтальная поверхность касаются расположенного в вертикальной плоскости обруча радиусом 30 см с центром в точке O. Небольшая шайба скользит вдоль наклонной плоскости из точки A. Какую минимальную начальную скорость надо сообщить шайбе, чтобы она оторвалась от опоры в точке B? Коэффициент трения между наклонной плоскостью и шайбой равен 0,2, угол = 30о. 4 м/с. 3. На укреплённой на столе полусфере радиуса r лежит небольшая шайба массой m. От незначительного толчка шайба начинает соскальзывать. Вследствие трения за время, в течение которого шайба скользила по полусфере, выделилось количество теплоты Q. 2 Q а) На какой высоте h шайба оторвалась от полусферы? h r . 3 mg б) На какой высоте h шайба оторвалась от полусферы, если выделившееся количество теплоты равно кинетической энергии шайбы в момент отрыва? r/2. 4. Небольшая шайба массой m соскальзывает с высоты H = 2r по гладкому жёлобу, переходящему в окружность радиуса r. а) На какой высоте h (по отношению к нижней точке окружности) шайба оторвётся от 5r жёлоба? h . 3 б) С какой силой шайба давит на жёлоб, когда она находится на одной горизонтали с центром окружности? 2 mg. 5. Какую скорость можно сообщить шарику в нижней точке, чтобы он начал совершать колебания, если: а) шарик подвешен на нити длиной l? v 2 gl . а) шарик подвешен на лёгком стрежне длиной l? v 2 gl . Подсказка. Шарик на нити не должен подняться выше точки подвеса, а шарик на стержне, не должен достичь верхней точки окружности.