Для самостоятельного решения
реклама
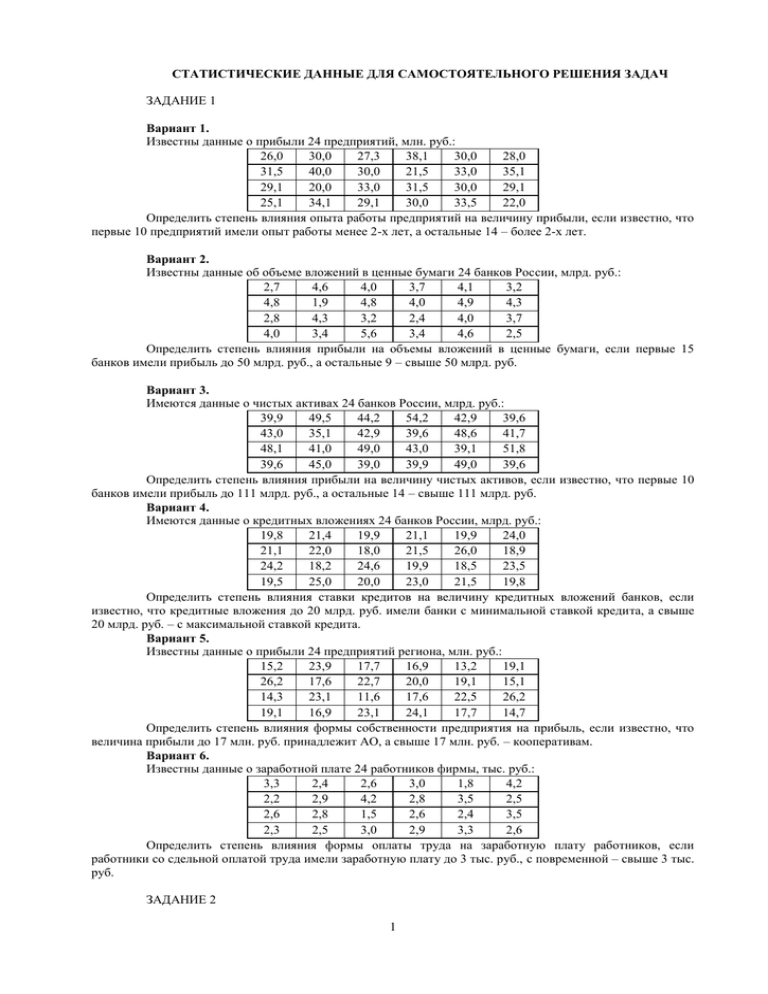
СТАТИСТИЧЕСКИЕ ДАННЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ЗАДАЧ ЗАДАНИЕ 1 Вариант 1. Известны данные о прибыли 24 предприятий, млн. руб.: 26,0 30,0 27,3 38,1 30,0 28,0 31,5 40,0 30,0 21,5 33,0 35,1 29,1 20,0 33,0 31,5 30,0 29,1 25,1 34,1 29,1 30,0 33,5 22,0 Определить степень влияния опыта работы предприятий на величину прибыли, если известно, что первые 10 предприятий имели опыт работы менее 2-х лет, а остальные 14 – более 2-х лет. Вариант 2. Известны данные об объеме вложений в ценные бумаги 24 банков России, млрд. руб.: 2,7 4,6 4,0 3,7 4,1 3,2 4,8 1,9 4,8 4,0 4,9 4,3 2,8 4,3 3,2 2,4 4,0 3,7 4,0 3,4 5,6 3,4 4,6 2,5 Определить степень влияния прибыли на объемы вложений в ценные бумаги, если первые 15 банков имели прибыль до 50 млрд. руб., а остальные 9 – свыше 50 млрд. руб. Вариант 3. Имеются данные о чистых активах 24 банков России, млрд. руб.: 39,9 49,5 44,2 54,2 42,9 39,6 43,0 35,1 42,9 39,6 48,6 41,7 48,1 41,0 49,0 43,0 39,1 51,8 39,6 45,0 39,0 39,9 49,0 39,6 Определить степень влияния прибыли на величину чистых активов, если известно, что первые 10 банков имели прибыль до 111 млрд. руб., а остальные 14 – свыше 111 млрд. руб. Вариант 4. Имеются данные о кредитных вложениях 24 банков России, млрд. руб.: 19,8 21,4 19,9 21,1 19,9 24,0 21,1 22,0 18,0 21,5 26,0 18,9 24,2 18,2 24,6 19,9 18,5 23,5 19,5 25,0 20,0 23,0 21,5 19,8 Определить степень влияния ставки кредитов на величину кредитных вложений банков, если известно, что кредитные вложения до 20 млрд. руб. имели банки с минимальной ставкой кредита, а свыше 20 млрд. руб. – с максимальной ставкой кредита. Вариант 5. Известны данные о прибыли 24 предприятий региона, млн. руб.: 15,2 23,9 17,7 16,9 13,2 19,1 26,2 17,6 22,7 20,0 19,1 15,1 14,3 23,1 11,6 17,6 22,5 26,2 19,1 16,9 23,1 24,1 17,7 14,7 Определить степень влияния формы собственности предприятия на прибыль, если известно, что величина прибыли до 17 млн. руб. принадлежит АО, а свыше 17 млн. руб. – кооперативам. Вариант 6. Известны данные о заработной плате 24 работников фирмы, тыс. руб.: 3,3 2,4 2,6 3,0 1,8 4,2 2,2 2,9 4,2 2,8 3,5 2,5 2,6 2,8 1,5 2,6 2,4 3,5 2,3 2,5 3,0 2,9 3,3 2,6 Определить степень влияния формы оплаты труда на заработную плату работников, если работники со сдельной оплатой труда имели заработную плату до 3 тыс. руб., с повременной – свыше 3 тыс. руб. ЗАДАНИЕ 2 1 Необходимо проанализировать производительность труда рабочих одного из цехов НПО “Виктория”. С этой целью была образована контрольная группа рабочих, имеющих стаж работы до 1 года, во вторую группу вошли рабочие со стажем от 1 до 3 лет и в третью группу объединили рабочих с большим стажем. Для чистоты эксперимента были сформированы пять групп, приблизительно равноценных по показателям. Результаты приведены в таблице 10. Таблица 10 Производительность труда рабочих цеха НПО “Виктория”, деталей за смену Повторность Номер Вариант опыта варианта 1 2 3 4 5 411 419 426 432 430 I группа (контр.) 460 472 478 480 470 1 II группа 475 440 500 482 495 III группа 278 285 200 256 291 I группа 330 319 344 336 327 2 II группа 378 388 391 387 399 III группа 426 440 434 442 437 I группа 540 535 560 550 552 3 II группа 552 546 564 558 560 III группа 511 519 526 532 530 I группа 560 572 578 580 570 4 II группа 575 540 600 582 595 III группа 464 470 472 468 480 I группа 478 482 500 498 502 5 II группа 530 536 540 527 534 III группа 328 336 327 319 329 I группа 423 426 411 409 411 6 II группа 456 462 468 470 457 III группа Пример 3. Дисперсионный анализ при группировке данных по двум признакам (неслучайное распределение повторностей в группе) Проанализировав результаты по реализации литературы (пример 2), правление фирмы пришло к выводу о необходимости продолжения эксперимента. Цель опыта состояла в том, чтобы уловить эффект взаимодействия между стажем работы и полом сотрудников. Участники эксперимента предварительно были разделены на 2 части (блока). Одну часть (блок) составляли одни мужчины, другую – женщины. Каждый блок включал в себя группы по стажу работы: контроль – проработавшие в этой сфере менее года, 1 гр. – со стажем 1 год, 2 гр. – соответственно – 2 года и 3 гр. – 3 и более лет. Опыт проведен в трехкратной повторности. Следовательно, распределение в каждом варианте неслучайное. Результаты эксперимента приведены в таблице 11. Таблица 11 Количество проданной научной литературы, шт. (в среднем за месяц) Средние Повторности Сумма Пол Вариант опыта xj xj 1 2 3 Женский Мужской Контроль Стаж: 133 154 134 421 140 1 год 2 года 3 года 162 200 240 735 184 211 171 214 217 756 189 186 179 210 229 752 188 190 512 624 686 2243 Х 587 171 208 229 Х 187 196 1 год 2 года 3 года 222 228 235 216 214 231 214 230 246 652 672 712 217 224 237 Суммы Средние по группе Контроль Стаж: 2 Х 219 Суммы Средние по группе 896 224 847 212 880 220 Суммы 1631 1603 1632 4866= 204 201 204 Х 203 172 170 162 Х 168 192 214 238 194 214 224 197 220 238 Х Х Х 194 216 233 x i Средние по повторностям Средние по подгруппам: Контроль Стаж: 1 год 2 года 3 года 2623 Х x ij Х Требуется оценить достоверность различий между средними по вариантам опыта, используя дисперсионный метод анализа. Решение. 1. Выдвигаем гипотезу о том, что факторы не оказывают влияния на реализацию литературы. Заключение по гипотезе сделаем с вероятностью 0,05. Количество реализуемой литературы варьировало в зависимости от пола, стажа работы, от сочетания этих факторов, от различий в составе групп, а так же не исключается случайное варьирование. Исходя из перечисленного, общую сумму квадратов отклонений следует представить как сумму: W0 Wпол Wстаж Wвзаим Wповт Wост Разложение проведем в два этапа. На первом этапе разложим: W0 Wфакт Wповт Wост ; а на втором - Wполстаж Wпол Wстаж Wвзаим . Определим число наблюдений. Анализируются 2 части (блока), т.е. k = 2. Второй фактор – стаж работы имеет 4 группы, l = 4. Каждый вариант представлен 3 повторами, т.е. n = 3. Общее число наблюдений N = k · l · n = 2 · 4 · 3 = 24. 2. Для упрощения вычислений выразим результаты эксперимента в отклонениях от постоянной величины А. За А принимается величина, близкая к общей средней (А = 200). Результаты занесем в таблицу 12. Таблица 12 Таблица отклонений Повторности Вариант Сумма yj Пол опыта 1 2 3 -67 -46 -66 -179 Контроль Стаж: -29 -21 -88 1 год -38 0 14 10 24 2 года 17 29 86 3 года 40 11 -14 -10 -13 Контроль Стаж: 16 14 52 1 год 22 14 30 72 2 года 28 31 46 112 3 года 35 Женский Мужской Сумма y i 31 3 32 66 y ij 3. Проверим правильность проведенных преобразований: x y ij ij N A, 4866 66 24 200 . Определим общую сумму квадратов, суммы квадратов всех вариантов опыта, повторностей: W0 Wполстаж Wповт Wост . Возводя в квадрат данные табл. 12, получим значения для определения Wполстаж и Wповт . Результаты вычислений поместим в таблицу 13: 3 Таблица 13 Таблица квадратов отклонений Повторности Сумма квадратов Вариант опыта Пол 1 2 3 4489 1444 0 1600 121 484 784 1225 2116 841 196 289 196 256 196 961 4356 441 100 841 100 196 900 2116 10147 5051 9050 961 9 1024 Женский Мужской Контроль 1 год 2 года 3 года Контроль 1 год 2 года 3 года Сумма квадратов yi2 y ( yij ) 2 10961 2726 296 2730 417 936 1880 4302 24248 Квадрат сумм ( yi ) 2 Квадрат сумм 2 j 1994 y 32041 7744 576 7396 169 2704 5184 12544 68358 2 ij ( y ) i 2 ( y 4356 ( y ij j )2 )2 Воспользуемся данными таблицы и рассчитаем: W0 y ij2 Wпол стаж ( y ij ) 24248 N ( y ( 2 n yi ) 2 j) 2 ( ( y y N ij ) 4356 24066 ,0 24 ij ) 2 68358 4356 22604 ,0 3 24 2 1994 4356 67 ,3 k l N 24 24 Wост W0 Wполстаж Wповт 24066 22604 67 ,3 1394 ,7 4. Определим число степеней свободы вариации: 0 N 1 24 1 23 Wповт пол ст k l 1 2 4 1 7 повт n 1 3 1 2 ост 0 пол ст повт 23 7 2 14 Проведем предварительный анализ дисперсий, разделив суммы квадратов отклонений на соответствующее число степеней свободы (табл. 14): Таблица 14 Предварительный анализ дисперсий Отношение Сумма Степень Источник дисперсий квадратов свободы Дисперсия вариации отклонений вариации Fфакт Fтабл 22604,0 7 3229,1 32,4 2,77 Пол + стаж 67,3 2 33,7 Х Х Повторности 1394,7 14 99,6 1 Х Остаточная 24066,0 23 X Общая ( Fтабл 5. По приложению А определяем Fтабл. При 5% уровне вероятности для 7 и 14 степеней свободы S2 7 пол2 ст ) F0,05 2,77 . 14 S ост 2 S пол ст 3229 ,1 32,4 . 2 99,6 S ост Проведя предварительный анализ существенности средних (Fфакт > Fтабл ), делаем вывод о достоверности различий в средних и целесообразности перехода к дальнейшим расчетам. Fфак 4 6. Приступим к рассмотрению вариации реализованной литературы, которая характеризуется различиями по полу, стажу и их взаимодействием. Для этого, используя суммы отклонений по повторностям (табл. 12), составим вспомогательную таблицу: Таблица 15 Отклонения по вариантам опыта Стаж работы, лет Пол Контроль Сумма 1 2 3 -179 -88 24 86 -157 Мужской -13 52 72 112 223 Женский -192 -36 96 198 66 Сумма 7. Результаты вычислений возведем в квадрат и занесем в таблицу: 5 Таблица квадратов отклонений по вариантам опыта Квадрат суммы Стаж работы, лет Контроль Сумма 2 1 2 3 Пол Мужской Женский 32041 169 7744 2704 676 5184 7396 12544 47857 20601 Сумма 32210 10448 5860 19940 68458 36864 1296 9604 39204 Квадрат сумм 8. 2 73754= 86968= 2 4624= 2 y 2 ij Полученная таблица квадратов позволяет установить: Wполстаж Wстаж Wпол Wвзаим Wполстаж 22604 ,0 (вычисление см. в п.3) Wстаж Wпол ( ' ' ) 2 k n ( ')2 ( ( y ln Wвзаим Wпол ст Wпол 9. 24025 49729 ij ) 2 N y ij ) 2 86968 4624 14302 ,0 23 24 73754 4624 5953 ,5 N 43 24 Wстаж 22604 ,0 5953 ,5 14302 ,0 2348 ,5 Определим число степеней свободы: пол k 1 2 1 1 стаж l 1 4 1 3 взаим k l 1 k 1 l 1 7 1 3 3 10. Перейдем к заключительному этапу анализа. Объединим результаты вычислений в общую таблицу: Таблица 17 Анализ дисперсий Источник вариации Пол Стаж Взаимодействие факторов Повторности Остаточная Общая Отношение Сумма Степень квадратов свободы Дисперсия дисперсий отклонений вариации Fфакт Fтабл 5953,5 1 5953,5 59,7 4,60 14302,0 3 4767,3 47,8 3,34 2348,5 3 782,8 7,8 3,34 67,3 1394,7 24066,0 2 14 23 33,7 99,8 X 0,3 1,0 X 3,74 X X Путем сопоставлений вычислим фактическое отношение дисперсий. За базу сравнения 2 принимается S ост . Например: Fфакт 2 S пол 2 S ост 5953 ,5 59,7 и т.д. 99,8 По таблице 5%-го уровня распределения F (см. приложение А) установим Fтабл (аналогично тому, как это было сделано в примере 2). Сопоставление Fфакт с Fтабл показывает, что существенны различия в среднем количестве реализуемой литературы по первому и второму факторам. Значительно менялось количество литературы и в результате взаимодействия факторов. Таким образом, приходим к выводу, что выдвинутая гипотеза о том, что различия в количестве реализуемой литературы случайны, должна быть отвергнута. Поскольку выдвинутая первоначально гипотеза на основании данных дисперсионного анализа отвергнута, следует оценить достоверность различий между парами средних. Для этого вычислим среднюю и предельную ошибки. m12 S ост 2 n 2 10 0,82 8,2 шт / в месяц, 3 10 6 E0.05 t m12 . При вероятности 0,05 и 14 степенях свободы вариации критическое значение нормированного отклонения t (см. приложение Б) составляет 2,1448 ≈ 2,14. Предельная ошибка: 0,05 t m12 2,14 8,2 17 ,5 шт. в месяц. Следовательно, величина возможных случайных колебаний при данном уровне вероятности не должна превышать 17,5 шт. в месяц. Определим существенность разности в количестве реализованной литературы. Выполним следующие сопоставления (см. табл. 11). x1 x 2 140 171 31 x1 x2 196 217 21 x1 x 3 140 208 68 x1 x3 196 224 28 x1 x 4 140 229 89 x1 x4 196 237 41 x 2 x 3 171 208 37 x2 x3 217 224 7 x 2 x 4 171 229 58 x2 x4 217 237 20 x 3 x 4 208 229 21 x3 x4 224 237 13 В первом блоке, который составили одни мужчины, все разности между средним количеством проданной литературы при меняющемся стаже работы существенны, так как превышают по абсолютной величине предельную ошибку ε 0,05=17,5 шт. в месяц. х 2 х 3 и х 3 х 4 Во втором блоке, представленном женщинами, две из шести разностей лежат в границах случайных колебаний. Несущественны разности х 2 х3 и х3 х 4 то есть увеличение стажа работы с одного года до двух и с двух до трех дают соответственно разности в количестве проданной литературы 7 и 13 шт. в месяц, что меньше предельной ошибки. Четыре из шести приведенных разностей больше 17,5 шт. в месяц и, следовательно, они существенны, а две – несущественны. Таким образом, в рассмотренном примере, когда анализируется работа женщин, несколько ослабляется воздействие стажа на объем проданной литературы. В целом же, в десяти случаях из двенадцати разности превышают по абсолютной величине предельную ошибку, что позволяет рассматривать их как существенные. СТАТИСТИЧЕСКИЕ ДАННЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ЗАДАЧ Проанализируйте производительность труда двух групп рабочих, чтобы выявить эффект перехода от работы на старом оборудовании к новому и стажем участников эксперимента. Оцените достоверность различий между средними по вариантам опыта, используя дисперсионный метод анализа. Данные для решения задачи представлены в таблице 18. 7 Таблица 18 Производительность труда (шт. за смену) Номер Оборудование варианта 1 Прежнее Новое 2 Прежнее Новое 3 Прежнее Новое 4 Прежнее Новое 5 Прежнее Новое 6 Прежнее Новое Стаж работы до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года до 1 года (контроль) 1 год 2 года 3 года 8 Повторности I 16,7 17,7 21,0 22,3 17,4 18,8 22,6 23,9 16,0 19,5 20,0 23,7 22,9 25,5 27,0 31,1 31,1 32,2 34,1 35,2 33,4 36,3 38,7 39,9 17,6 18,9 22,4 23,7 22,6 25,5 26,8 31,1 17,0 20,5 21,0 24,7 31,3 32,4 34,3 35,2 14,3 15,3 19,0 20,3 15,3 16,8 20,5 21,7 II 16,6 18,1 21,1 22,6 16,9 18,6 23,1 23,7 18,4 28,0 21,3 22,4 22,6 28,5 28,8 29,5 29,4 30,3 33,0 35,2 32,0 35,9 37,2 40,4 16,7 18,5 23,3 23,6 22,3 28,5 28,6 29,5 19,4 29,0 22,3 22,4 29,6 30,5 33,2 35,7 14,2 16,0 19,1 20,6 14,8 16,5 21,0 21,5 III 16,2 17,4 20,1 22,5 17,6 19,8 22,9 23,8 16,8 18,9 21,7 23,9 21,6 25,7 30,0 31,2 27,2 29,4 33,4 35,9 31,5 34,1 37,3 40,2 17,8 19,8 22,7 24,0 21,3 25,7 29,9 31,2 17,8 19,9 22,7 24,4 27,4 29,6 33,6 35,6 15,8 17,2 18,1 20,5 15,5 17,7 20,8 21,6

