Тренировочная работа № 1

Тренировочная работа № 1
(без логарифмов)
Ответом в заданиях В1—В12 является целое число или число, записанное в виде десятичной
дроби. Укажите ответ в отведённом для него поле. Единицы измерения в ответе не пишите.
В1.
Летом килограмм клубники стоит 90 руб. Мама купила 1 кг500 г клубники. Сколько
рублей сдачи она должна получить с1000 руб.?
Ответ:
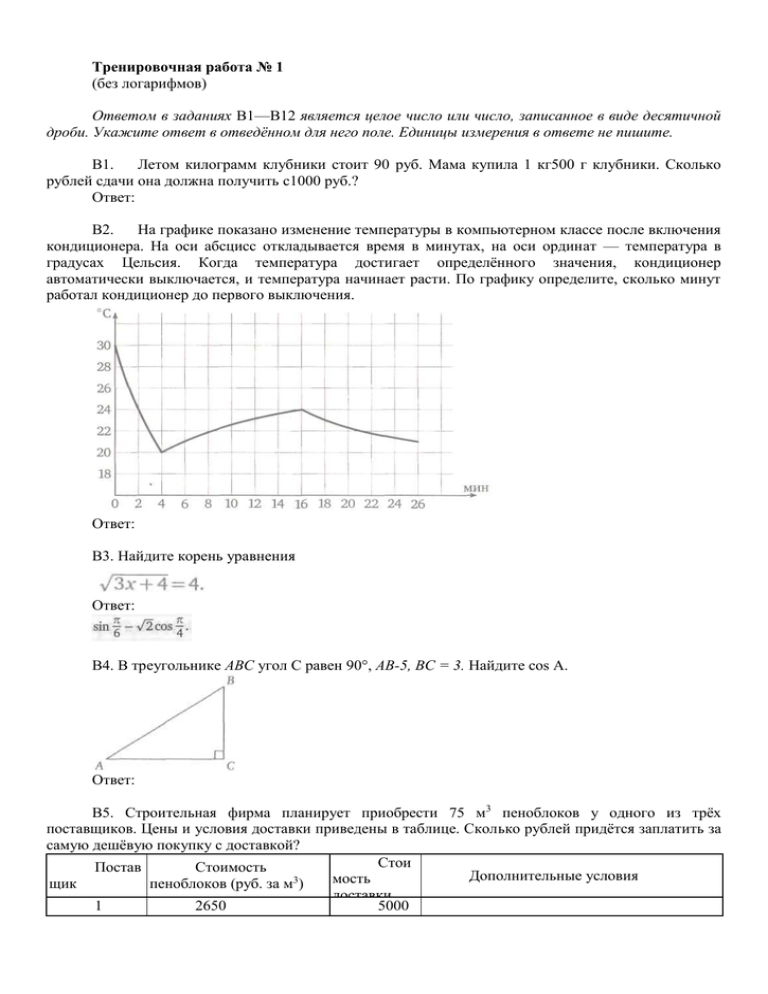
В2.
На графике показано изменение температуры в компьютерном классе после включения
кондиционера. На оси абсцисс откладывается время в минутах, на оси ординат — температура в
градусах Цельсия. Когда температура достигает определённого значения, кондиционер
автоматически выключается, и температура начинает расти. По графику определите, сколько минут
работал кондиционер до первого выключения.
Ответ:
В3. Найдите корень уравнения
Ответ:
В4. В треугольнике ABC угол С равен 90°, АВ-5, ВС = 3. Найдите cos A.
Ответ:
В5. Строительная фирма планирует приобрести 75 м3 пеноблоков у одного из трёх
поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей придётся заплатить за
самую дешёвую покупку с доставкой?
Стои
Постав
Стоимость
Дополнительные условия
3
мость
щик
пеноблоков (руб. за м )
доставки
1
2650
5000
руб.
2
2900
1000
При заказе на сумму больше 150000
руб. доставка бесплатно
4900
При заказе на сумму больше 200 000
руб. доставка бесплатно
руб.
3
2700
руб.
Ответ:
В6. Бумага разграфлена на квадратные клетки размером 1 см х 1 см. Найдите площадь
треугольника, изображённого на рисунке. Ответ дайте в квадратных сантиметрах.
Ответ:
В7. Найдите значение выражения
Ответ:
В8. На рисунке изображён график производной y = f'(x) функции y = f(x). В какой точке
отрезка [-5; 0] функция у = f(х) достигает своего наименьшего значения?
Ответ:
В9. Камень брошен вниз с высоты 36 м. Пока камень не упал, его высоту можно находить по
формуле h{t) = 36 - 3t - 5t2 (h — высота в метрах, t — время в секундах, прошедшее с момента
броска). Сколько секунд камень будет падать?
Ответ:
В10. Площадь поверхности прямоугольного параллелепипеда равна 1. Чему будет равна
площадь поверхности параллелепипеда, если каждое его ребро увеличить в три раза?
Ответ:
В11.
Найдите точку максимума функции
Ответ:
В12. Маша и Настя могут вымыть окно за 20 мин. Настя и Лена могут вымыть это же окно за
15 мин, а Маша и Лена — за 12 мин. За какое время девочки вымоют окно, работая втроём? Ответ
дайте в минутах.
Ответ:
При выполнении заданий С1—С6 необходимо записать решение.
C1. Решите систему уравнений
С2. К диагонали А1С куба ABCDA1B1C1D1 провели перпендикуляры из середин рёбер АВ и AD.
Найдите угол между этими перпендикулярами.
С3. Решите неравенство
С4. Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найдите радиус окружности,
касающейся этой прямой и сторон угла.
С5. Найдите все значения а, при каждом из которых уравнение
имеет ровно восемь различных решений.
С6. Найдите наибольшее натуральное п, для которого число
делится на каждое из чисел кк при к = 1 ,2 ,..., п.
Тренировочная работа № 16
(без производной)
Ответом в заданиях В1—В12 является целое число или число, записанное в виде десятичной
дроби. Укажите ответ в отведённом для него поле. Единицы измерения в ответе не пишите.
В1.
Магазин открывается в 10 часов утра, а закрывается в 10 часов вечера. Обеденный
перерыв длится с 15 до 16 часов. Сколько часов в день открыт магазин?
Ответ:
В2.
На графике показано изменение давления в паровой турбине после запуска. На оси
абсцисс откладывается время в минутах, на оси ординат – давление в атмосферах. Когда давление
достигает определённого значения, открывается клапан, выпускающий часть пара, и давление
падает. Затем клапан закрывается, и давление снова растёт. Определите по графику, при каком
давлении открывается клапан. Ответ дайте в атмосферах.
Ответ:
В3. Найдите корень уравнения
Ответ:
В4. Найдите
Ответ:
В5. На рисунке показана схема дорог и расстояние между пунктами А, В, С, D и Е вдоль этих
дорог (в километрах).
Из Е в А самым длинным путём маршрутное такси едет ровно полтора часа. Если такси едет
самым коротким путём, то тратит на дорогу один час и десять минут. Но есть ещё один путь,
который занимает один час пятнадцать минут. Водитель выбирает маршрут так, чтобы можно было
ехать с наименьшей средней скоростью. Какой будет эта средняя скорость? Ответ дайте в
километрах в час.
В6. Бумага разграфлена на квадратные клетки размером 1 см х 1 см. Найдите площадь
треугольника, изображённого на рисунке. Ответ дайте в квадратных сантиметрах.
Ответ:
В7. Найдите значение выражения
Ответ:
В8. На рисунке изображён график движения самолёта по маршруту. По горизонтальной оси
откладывается время, по вертикальной — пройденное самолётом расстояние от начала маршрута.
Вычислите среднюю скорость движения самолёта по маршруту. Ответ дайте в километрах в час.
Ответ:
В9. Камень брошен вниз с высоты 64 м. Пока камень не упал, его высоту можно находить по
формуле
(h – высота в метрах, t — время в секундах, прошедшее с момента
броска). Сколько секунд камень будет падать?
Ответ:
В10. Объём прямоугольного параллелепипеда равен 24. Чему будет равен объём
параллелепипеда, если каждое его ребро уменьшить в два раза?
Ответ:
В11.
Решите уравнение
Если корней несколько, в ответ запишите наименьший корень.
Ответ:
В12. Садовый насос перекачивает 9 л воды за 4 минуты. Дополнительно включили второй
насос, перекачивающий тот же объём воды за 7 минут. Сколько минут эти два насоса должны
работать совместно, чтобы перекачать 99 л воды?
Ответ:
При выполнении заданий С1—С6 необходимо записать решение.
С1. Решите систему уравнений
С2. Диагональ A’C куба ABCDA’B’C’D’ служит ребром двугранного угла, грани которого
проходят через вершины В и D. Найдите величину этого угла.
С3. Решите неравенство
С4. Противолежащая основанию вершина равнобедренного треугольника с боковой стороной
5 и основанием 8 служит центром данной окружности радиуса 2. Найдите радиус окружности,
касающейся данной и проходящей через концы основания треугольника.
С5. Найдите все значения а, при каждом из которых уравнение
имеет ровно один корень.
С6. Найдите наименьшее натуральное п, для которого число
не делится на пп.
Диагностическая работа №9
Часть 1
Ответом на задания В1-В12 должно быть целое число или конечная десятичная дробь.
Ответ следует записать в бланк ответов №1 справа от номера выполняемого задания, начиная с
первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в
соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно.
В1.
В туристический поход отправляется группа из 18 человек. В походе на одного
человека приходится 60 грамм гречки на прием пищи. Планируется 7 раз готовить гречку. Сколько
килограммовых пачек необходимо купить, чтобы гречки хватило?
Ответ:
В2.
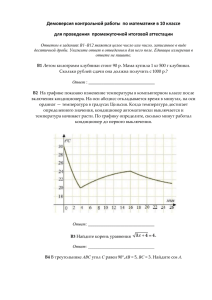
На графике, изображенном на рисунке, представлено изменение биржевой стоимости
акций горнодобывающей компании в первой половине сентября. 7 сентября бизнесмен купил пакет
акций, а 13 сентября продал его. В результате этих операций прибыль бизнесмена составила 3600
рублей. Сколько акций было в пакете?
Ответ:
В3. Решите уравнение
Ответ:
В4.
В треугольнике ABC угол С равен 90°, АВ = 102, cos A =
Ответ:
Найдите ВС.
В5.
Ткань можно покупать либо по метру, стоимостью 23 рубля за метр, либо рулонами по
100 метров, стоимостью 1950 рублей за рулон. Сколько рублей придется заплатить за самый
дешевый вариант приобретения 80 метров ткани?
Ответ:
В6.
Найдите площадь треугольника ABC.
Ответ:
В7. Найдите значение выражения
Ответ:
В8. На рисунке изображен график функции y = f(x). Прямая, проходящая через точку (7; 1),
касается этого графика в точке с абсциссой 3. Найдите f'(3).
Ответ:
В9. Прямоугольный параллелепипед описан около сферы радиуса 4. Найдите его объем.
Ответ:
В10. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для
нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом
интервале температур задается выражением T(t) = T0 + at + bt2, где Т0 = 900 К, а = 31 К/мин, b == –
0,2 К/мин2. Известно, что при температурах нагревателя свыше 1550 К прибор может испортиться,
поэтому его нужно отключать. Определите (в минутах), через какое наибольшее время после начала
работы нужно отключать прибор.
Ответ:
В11.
Найдите наименьшее значение функции
на отрезке [6; 8].
Ответ:
В12. Смешали 14 литров 30-процентного водного раствора некоторого вещества с 10 литрами
18-процентного раствора этого же вещества. Сколько процентов составляет концентрация
получившегося раствора? Знак % в ответе не пишите.
Ответ:
Диагностическая работа №9
Часть 2
Для записи решений и ответов на задания С1-С6 используйте бланк ответов №2. Запишите
сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
С1. Решите систему уравнений
С2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины ребер: АА\ = 5, АВ =
12, AD = 8. Найдите тангенс угла между плоскостью ABC и плоскостью, проходящей через точку В
перпендикулярно прямой АК, если К — середина ребра C1D1.
С3. Решите неравенство
С4. Окружности с центрами О и В радиуса ОВ пересекаются в точке С. Радиус ОА окружности
с центром О перпендикулярен ОВ, причем точки А и С лежат по одну сторону от прямой ОВ.
Окружность Si касается меньших дуг АВ и ОС этих окружностей, а также прямой О А, а окружность
S2 касается окружности с центром В, прямой О А и окружности Si. Найдите отношение радиуса
окружности S1 к радиусу окружности S2.
С5. Найдите все значения параметра а, при каждом из которых все корни уравнения
удовлетворяют неравенству
С6. Решите в целых числах уравнение