Вариант решения задания №3

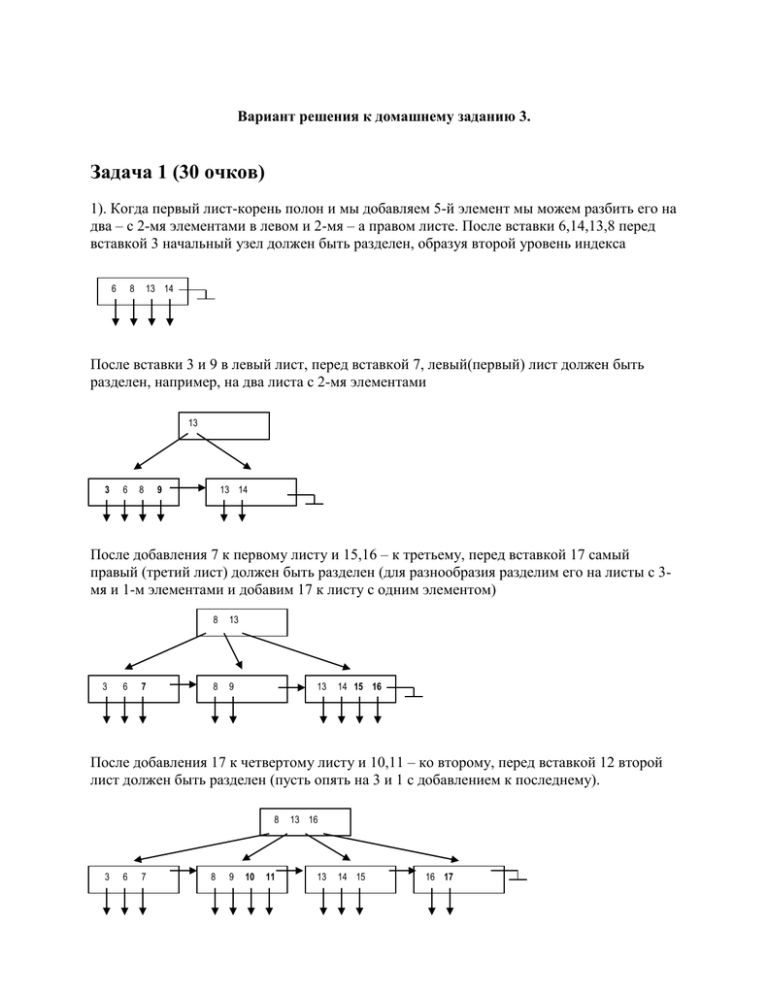
Вариант решения к домашнему заданию 3.
Задача 1 (30 очков)
1). Когда первый лист-корень полон и мы добавляем 5-й элемент мы можем разбить его на
два – с 2-мя элементами в левом и 2-мя – а правом листе. После вставки 6,14,13,8 перед
вставкой 3 начальный узел должен быть разделен, образуя второй уровень индекса
6
8
13 14
После вставки 3 и 9 в левый лист, перед вставкой 7, левый(первый) лист должен быть
разделен, например, на два листа с 2-мя элементами
13
3
6
8
9
13 14
После добавления 7 к первому листу и 15,16 – к третьему, перед вставкой 17 самый
правый (третий лист) должен быть разделен (для разнообразия разделим его на листы с 3мя и 1-м элементами и добавим 17 к листу с одним элементом)
3
6
7
8
13
8
9
13
14 15 16
После добавления 17 к четвертому листу и 10,11 – ко второму, перед вставкой 12 второй
лист должен быть разделен (пусть опять на 3 и 1 с добавлением к последнему).
8
3
6
7
8
9
10
11
13 16
13
14 15
16 17
После добавления 12 к третьему и 1 – к первому, перед вставкой 2 первый лист должен
быть разделен (пусть пополам), корень тоже должен быть разделен, образуя третий
уровень индекса
8
1
3
6
7
8
9
10
11 13 16
11 12
13
14 15
16 17
Следующее дерево получаем добавлением 2 к первому листу, 18,19 – к (уже, после
деления 1-го) 6-му, 4 – опять к первому, и перед вставкой 20 последний (6-й) лист должен
быть разделен, Для экономии места и времени я не рисовал указатели на данные на
следующей странице.
11
1
2
3
4
6
8
6
7
13 16
8
9
10
11 12
13
14 15
16 17 18
19
Это – перед вставкой 5, первый лист должен быть разделен
11
1
2
3
4
6
8
6
7
13 16 19
8
9
10
11 12
13
Это - окончательное дерево.
4
1
2
3
4
5
6
14 15
16 17 18
19
20
11
8
13 16 19
6
7
8
9
10
11 12
13
14 15
16 17 18
19
20
При вставке 12 вместо разделения блока можно было бы вставить это значение в следующий
блок справа. Это потребевало бы больше работы по изменению промежуточных узлов, но
сократило бы число тисьев в окончательном дереве с 8 до 6.
12
1
2
3
4
5
8
5
6
7
8
9
10
11
12
13
14
15
16
19
16
17
18
19
20
2). После удаления Q, получим
R
D J N
AB
DEF
U Y
JKL
NO
RS
UV
YZ
Далее, после удаления N
R
D J
AB
DEF
U Y
JKLO
RS
UV
YZ
При удалении N можно было переместить O в соседний лист справа, в этом случае
потребовались бы изменения в корне и правом промежуточном листе. Наконец, после
удаления V
D J RY
AB
DEF
JKLO
RS U
YZ
Здесь перенос U влево или вправо требует, практически, того же объема работы.
Задача 2 (25 очков).
a). Поскольку данные и индекс занимают непрерывную память на диске, нам не нужны
указатели для индекса, за исключением первого, указывающего на первый блок данных
(Предполагается, что мы знаем адрес первого блока индекса). Адрес k-го блока данных
может быть вычислен на основе позиции k-го ключа в индексе. Таким образом, первый блок
индекса будет содержать один указатель (длиной 8 байт) на первый блок данных и
floor((4096-8)/12 ) = 340 ключевых значений, где floor() – целая часть снизу . Остальные
индексные блоки будут содержать floor(4096/12) = 341 ключей. Следовательно, общий
размер разреженного одно-уровнего индекса будет 1 + ceil(4000000-340)/341) = 11731
блоков, где ceil() – целая часть сверху.
б). Поскольку данные и индекс не являются непрерывными на диске, мы должны хранить
указатель для каждого ключа и один указатель на следующий индексный блок, за
исключением, быть может, последнего индексного блока. Одна пара (ключ, указатель)
занимает 12+8=20 байт. Один индексный блок может содежать floor( (4096-8)/20 ) =
204 ключа. Следовательно, общий размер разреженного одно-уровнего индекса будет
ceil( 4000000/204 ) = 19608 блоков.
в). Для минимизации используемого пространства, предположим, что индекс второго уровня
– разреженный и непрерывный на диске. Поскольку каждый блок индекса первого уровня
требует одного указателя, то во втором уровне каждый блок будет иметь floor(4096/20) = 204
ключа, и размер этого индекса будет ceil(19608/204) = 97 блоков.
г). Вторичный индекс должен быть плотным. Предположим также, что указательадресует
запись, а не блок данных. Тогда один индексный блок может хранить floor( 4096/(12+9) ) =
195 ключей. Поскольку каждая из 40000000 записей будет иметь соответствующий ключ в
этом индексе, его размер будет ceil( 40000000/195 ) = 205129 блоков. Если использовать
указатели на блоки, то блок индекса может хранить ( 4096/(12+8) ) = 204 ключа, и размер
индекса будет ceil( 40000000/204 ) = 196079 блоков
д). Индекс второго уровня для г) может быть разреженным и непрерывным. Для
минимизации пространства предположим, что индекс первого уровня непрерывен. Тогда
второй уровень может иметь только один указатель на первый блок первого. Первый блок
индекса второго уровня может храить 341 ключей, остальные – 341 (см.пункт а) ). Чтобы
адресовать 205129 блоков первого уровня (адресуются записи) нам потребуется
1+ceil((205129-340)/341) = 602 блока. Если первый уровень адресует блоки данных, то
индекс второго уровня потребует 1+ ceil((196079-340)/341) = 576 блоков.
Задача 3 (25 очков)
Пусть Т1 – время, требуемое для чтение одного блока в память, Т2 – время обработки блока в
памяти. Если для поиска записи в заданным ключом требуется проверить n блоков, то время
поиска будет n*(Т1 + Т2). В зависимости от порядка m двоичного дерева обозначим время
поиска через t(m) = logm(N) ((70+0.05*m )+ (a + b*log2(m))). Поскольку величина a<<70,
можем ее проигнорировать и записать, переходя к натуральному логарифму,
t(m) = ln(N)/ln(m)*(70+0.05*m + b*ln(m)* log2(e)) =
= ln(N)*(70+0.05*m)/ln(m) + ln(N)*b/ln(2)
Поскольку последнее слагаемое не зависит от m, нам нужно минимизировать функцию
f(m) = (70+0.05*m)/ln(m) = (1400 + m) /(20*ln(m))
Дифференцируя, получим
f’(m) = (ln(m) – (1400+m)/m)/(20*ln(m)*ln(m))
Пусть Mopt – корень уравнения f’(m) = 0. Легко заметить, что Mopt будет точкой минимума
функции f(m) поскольку ln(m) монотонно возрастает от 0 когда m=1 до +бесконечности, в то
время как (1400+m)/m монотонно убывает от 1401 до 1, следовательно производная f’(m) –
отрицательна в интервале 1<m<Mopt и положительна при Mopt<m. Поэтому f(m) (вместе с
t(m) ) уменьшается при 1<m<Mopt и возрастает при Mopt<m. Другими словами Mopt
является точкой глобального минимума для функции f(m).
Корень может быть найден приблизительно, например, методом «простой итерации». Для
g(x)=x, возьмем произвольное x0 и найдем x1 = g(x0), затем x2 = g(x1) и т.д. При
определенных условиях последовательность { xi } будет сходиться к корню уравнения
g(x)=x (его в этом случае еще называют «неподвижной точкой» для функции g(x)). Если
переписать наше уравнение в эквивалентной форме
m = (1400 + m)/ln(m)
и положить m0=100, получим
m1=1500/ln(100)=1500/4.605=325.72,
m2=1725.72/ln(325.72)=1725.72/5.786=298.26
m3=1698.26/ln(298.26)=1698.26/5.698=298.05
Похоже, что 298 очень близко к корню, а следовательно – и к минимуму функции f(m).
Вычислим f(m) в точках слева и справа от 298
f(297) = 1697/(20*ln(297)) = 14.9023519,
f(298) = 1698/(20*ln(298)) = 14.9023358,
f(299) = 1699/(20*ln(299)) = 14.9023491.
Следовательно, оптимальное количество указателей в блоке Mopt=298.
Пусть Ts – суммарное время поиска и задержки (в нашем случае Ts =70). Тогда
f’(m)= (ln(m) –(20*Ts+m)/m)/(20*ln(m)*ln(m))
Можно заметить, что чем меньше значение Ts, тем ниже график функции (20*Ts+m)/m и
тем рань ше он пересекается графиком ln(m). Следовательно, когда Ts уменьшается,
оптимальное значение Mopt также должно уменьшаться. Вычислим его для Ts=35 начиная с
m0=100:
m1 = (700+100)/ln(100) = 800/4.605 = 173.72
m2 = 873.72/ln(173.72) = 169.409
m3 = 869.41/ln(169.41) = 169.399
Оптимальное значение в этом случае Mopt=169.
Задача 4.
a). Пусть NPtrMin(j) минимальное число указателей на данные из B+ tree индекса, имеющего
j уровней.
Для j=1 это 1.
Для j=2 доолжно быть, по крайней мере, 2 листа, каждый из которых имеет не меньше, чем
Pl(n) = floor((n+1)/2) указателей на данные. Поэтому, NPtrMin(2) = 2*floor((n+1)/2). Для
каждого j>2 у нас будет (j-2) промежуточных уровня (не корень и не лист). Каждый узел
промежуточного уровня имеет не меньше Pi(n) = ceil((n+1)/2) указателей на более низкий
уровень (потомков), поэтому общее число прометочных узлов – не менее 2 * Pi(n)(j-2). Таким
образом, общее минимальное число указателей на данные будет
NPtrMin(j) = 2*(Pi(n)(j-2))*Pl(n) = 2*( ( ceil( (n+1)/2 ) )(j-2))*floor( (n+1)/2 ).
б). Минимальное число указателей на данные, определенное в а) для махсимального числа
уровней Jmax не может превышать число записе r, следовательно
r >= NptrMin(Jmax) = 2*(Pi(n))(Jmax-2))*Pl(n) или r/(2*P1(n)) >= (Pi(n))(Jmax-2)
Логарифмируя обе части неравенства, получим
ln(r/(2*Pl(n)) >= ln(Pi(n)) * (Jmax-2)
отсюда
ln(r/(2*floor((n+1)/2))
Jmax <= 2 + ---------------------------.
ln(ceil((n+1)/2))
Например, для r=230, что составляет более, чем 1000000000 записей, и n=127=27-1, будем
иметь Jmax<=2+(30-7)/6=5.88, что означает, что B+ tree не может иметь более, чем 5
уровней.