А1. Установите соответствие между изображениями и названиями этих фигур:
реклама
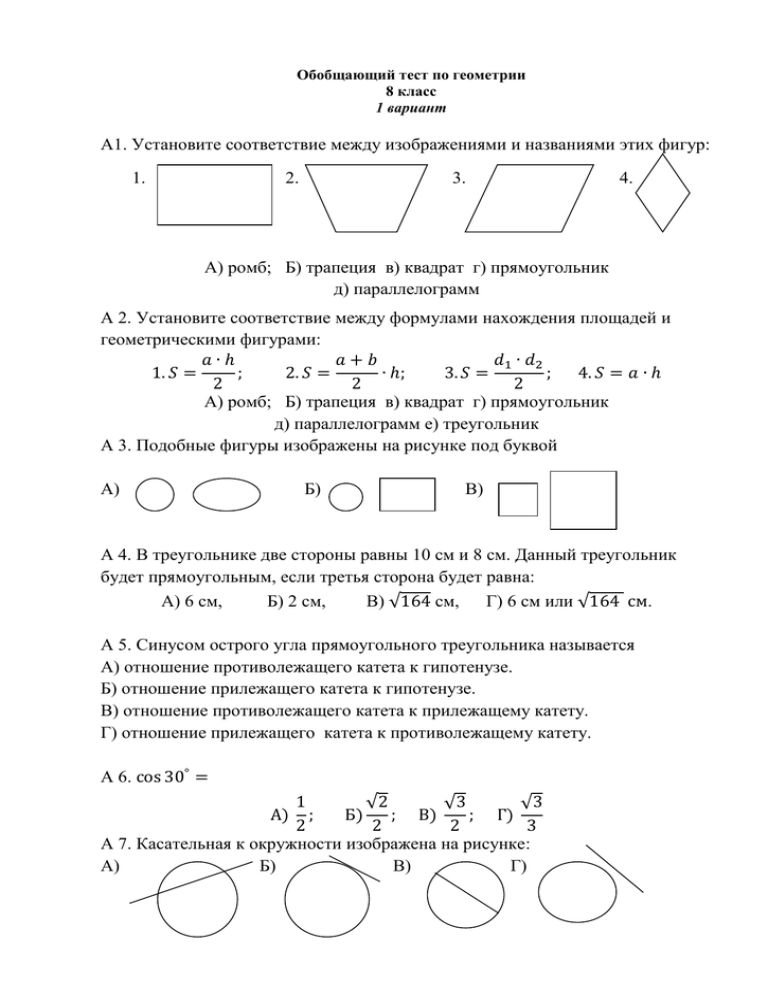
Обобщающий тест по геометрии 8 класс 1 вариант А1. Установите соответствие между изображениями и названиями этих фигур: 1. 2. 3. 4. А) ромб; Б) трапеция в) квадрат г) прямоугольник д) параллелограмм А 2. Установите соответствие между формулами нахождения площадей и геометрическими фигурами: 𝑎∙ℎ 𝑎+𝑏 𝑑1 ∙ 𝑑2 1. 𝑆 = ; 2. 𝑆 = ∙ ℎ; 3. 𝑆 = ; 4. 𝑆 = 𝑎 ∙ ℎ 2 2 2 А) ромб; Б) трапеция в) квадрат г) прямоугольник д) параллелограмм e) треугольник А 3. Подобные фигуры изображены на рисунке под буквой А) Б) В) А 4. В треугольнике две стороны равны 10 см и 8 см. Данный треугольник будет прямоугольным, если третья сторона будет равна: А) 6 см, Б) 2 см, В) √164 см, Г) 6 см или √164 см. А 5. Синусом острого угла прямоугольного треугольника называется А) отношение противолежащего катета к гипотенузе. Б) отношение прилежащего катета к гипотенузе. В) отношение противолежащего катета к прилежащему катету. Г) отношение прилежащего катета к противолежащему катету. А 6. cos 30° = 1 √2 √3 √3 ; Б) ; В) ; Г) 2 2 2 3 А 7. Касательная к окружности изображена на рисунке: А) Б) В) Г) А) А 8. Вписанный угол изображен на рисунке: О А 9. Центр вписанной окружности в треугольник совпадает А) с точкой пересечения биссектрис треугольника; Б) с точкой пересечения медиан треугольника; В) с точкой пересечения высот треугольника; Г) с точкой пересечения серединных перпендикуляров треугольника. А 10. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполнятся следующее равенство: А) ∠A+∠B = ∠D+∠C; Б) AB+CD = BC+AD; B C В) ∠A+∠C = ∠D+∠B; Г) AD · BC = AB · CD. A D В 1. Периметр ромба АВСD равен 20 см. Тогда сторона ромба равна ________ В 2. В прямоугольнике АВСD смежные стороны равны 3см и 4 см. Тогда площадь прямоугольника равна____ В 3. В прямоугольном треугольнике катеты равны 4 см и 5 см. Тогда гипотенуза в этом треугольнике равна______ В 4. На рисунке XY – средняя линия треугольника АВС. XY=6 см. Тогда АВ =_____ В X А Н Y B 5. cos 𝛼 = 5 13 С , 0 < 𝛼 < 90°. Тогда sin ∝ = С 1. В равнобедренном треугольнике боковые стороны равны 15 см, а высота, опущенная на основание, равна 12 см. Найти радиус вписанной в треугольник окружности. Обобщающий тест по геометрии 8 класс 2 вариант А1. Установите соответствие между изображениями и названиями этих фигур: 1. 2. 3. 4. А) ромб; Б) трапеция; в) треугольник; г) окружность; д) параллелограмм А 2. Установите соответствие между формулами нахождения площадей и геометрическими фигурами: 𝑎∙ℎ 𝑎+𝑏 𝑑1 ∙ 𝑑2 1. 𝑆 = ; 2. 𝑆 = ∙ ℎ; 3. 𝑆 = ; 4. 𝑆 = 𝑎 ∙ 𝑏 2 2 2 А) ромб; Б) трапеция; в) квадрат; г) прямоугольник; д) параллелограмм; e) треугольник А 3. Подобные фигуры изображены на рисунке под буквой А) Б) В) А 4. В треугольнике две стороны равны 8 см и 6 см. Данный треугольник будет прямоугольным, если третья сторона будет равна: А) 10 см, Б) 2 см, В) √28 см, Г) 10 см или √28 см. А 5. Косинусом острого угла прямоугольного треугольника называется А) отношение противолежащего катета к гипотенузе. Б) отношение прилежащего катета к гипотенузе. В) отношение противолежащего катета к прилежащему катету. Г) отношение прилежащего катета к противолежащему катету. А 6. cos 60° = 1 √2 √3 √3 ; Б) ; В) ; Г) 2 2 2 3 А 7. Секущая к окружности изображена на рисунке: А) Б) В) Г) А) А 8. Центральный угол изображен на рисунке: О А 9. Центр описанной окружности около треугольника совпадает А) с точкой пересечения биссектрис треугольника; Б) с точкой пересечения медиан треугольника; В) с точкой пересечения высот треугольника; Г) с точкой пересечения серединных перпендикуляров треугольника. А 10. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполнятся следующее равенство: А) ∠A+∠B = ∠D+∠C; Б) AB+CD = BC+AD; B C В) ∠A+∠C = ∠D+∠B; Г) AD + AB = BC + CD. A D В 1. Периметр квадрата АВСD равен 24 см. Тогда сторона ромба равна ______ В 2. В треугольнике АВС сторона равна 10см. а высота опущенная к ней 6 см. Тогда площадь треугольника равна____ В 3. В прямоугольном треугольнике катеты равны 5 см и 12 см. Тогда гипотенуза в этом треугольнике равна______ В 4. На рисунке XY – средняя линия треугольника АВС. AB = 14 см. Тогда XY =_____ В X А Н Y B 5. cos 𝛼 = 12 13 С , 0 < 𝛼 < 90°. Тогда sin 𝛼 = С 1. В равнобедренном треугольнике боковые стороны равны 15 см, а высота, опущенная на основание, равна 12 см. Найти радиус описанной около треугольника окружности.