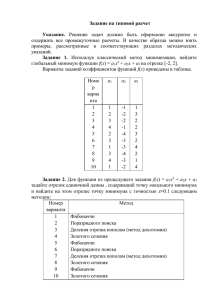
Задача 1. По обучающей выборке x -1 0 0 1 2 y 1

Задача 1.
По обучающей выборке
x
y
−1
0
1 −2
0
1
1
7
2
8
Методом наименьших квадратов построить модель вида f (x) = β0 + β1 x + β2 x2 .
Решение.
Составляем матрицу X и вектор y:




1 −1
1
1
 1
 −2 
0
0 




,
 1 .
1
0
0
X=
y
=




 1
 7 
1
1 
1
2
4
8
Имеем

5
X⊤ X =  2
6

2
6
6
8 ,
8 18


15
X⊤ y =  22  .
40
Решая систему нормальных уравнений X⊤ Xβ = X⊤ y, находим
 
1
β= 2 
1
Таким образом, нашли модель 1 + 2x + x2 .
Построить модель того же вида методом ридж-регрессии с параметром регуляризации λ = 2.
Решение.
Для λ = 2 получаем


7
2
6
8
8 .
X⊤ X + λI =  2
6
8 20
Решая регуляризованную систему нормальных уравнений (X⊤ X + λI)β = X⊤ y, находим


21/31
β =  81/62  .
79/62
Таким образом, нашли модель
79
21 81
+ x + x2 .
31 62
62
Задача 2. Дана обучающая выборка:
x1
x2
y
0
4
0
2 1
4 3
0 0
1 1 2
5 4 1
0 0 1
4 4
0 2
1 1
4 6
1 1
1 1
1. Изобразить объекты обучающей выборки в пространстве признаков x1 , x2 ;
2. с помощью линейного дискриминантного анализа для каждого класса построить дискриминантные функции
и записать уравнение разделяющей поверхности; изобразить поверхность;
3. с помощью квадратичного дискриминантного анализа для каждого класса построить дискриминантные функции;
4. найти уравнение оптимальной разделяющей гиперплоскости; нарисовать ее; указать опорные точки.
Решение.
Оцениваем вероятности классов:
c {Y = 1} = 1 .
Pr
2
c {Y = 0} = 1 ,
Pr
2
Оцениваем средние для классов:
µ
b0 =
1
4
µ
b1 =
,
Выборочные матрицы ковариации для каждого класса:
X
1
1
2 0
b0 =
Σ
,
(x(i) − µ
b0 )(x(i) − µ
b0 )⊤ =
0 2
N0 − 1
4
b1 =
Σ
y (i) =0
4
1
X
1
1
8
(x(i) − µ
b1 )(x(i) − µ
b1 )⊤ =
0
N1 − 1 (i)
4
y
=1
0
2
.
Оцениваем матрицу ковариации:
b =
Σ
X X
1
1
8
2 0
+
(x(i) − µ
bk )(x(i) − µ
bk )⊤ =
0
0 2
N −K
8
(i)
k y
=k
Находим
b −1 =
Σ
0
2 0
0 2
b −1 =
Σ
1
,
Линейные дискриминантные функции:
1/2
0
0
2
,
0
2
b −1 =
Σ
=
1
8
4/5
0
10
0
0
2
0
4
=
5/4
0
0
1/2
.
.
1 ⊤ b −1
c {Y = 0} = 4 x1 + 8x2 − 82 − ln 2,
b −1 µ
δ0 (x) = x⊤ Σ
b0 − µ
b0 + ln Pr
b Σ µ
2 0
5
5
1 ⊤ b −1
c {Y = 1} = 16 x1 + 2x2 − 37 − ln 2.
b −1 µ
δ1 (x) = x⊤ Σ
b Σ µ
b1 − µ
b1 + ln Pr
2 1
5
5
Разделяющая поверхность — прямая с уравнением δ0 (x) = δ1 (x) (красная прямая на графике):
4x1 − 10x2 + 15 = 0.
Квадратичные дискриминантные функции:
1
c {Y = 0} = −x2 + 2x1 − x2 + 8x2 − 17,
b 0 − 1 (x − µ
b −1 (x − µ
δ0 (x) = − ln det Σ
b0 )⊤ Σ
b0 ) + ln Pr
1
2
0
2
2
1
c {Y = 1} = − 1 x2 + 2x1 − x2 + 2x2 − 5 − ln 2.
b 1 − 1 (x − µ
b −1 (x − µ
b1 )⊤ Σ
b1 ) + ln Pr
δ1 (x) = − ln det Σ
2
1
2
2
4 1
Разделяющая поверхность — парабола с уравнением (синяя кривая на графике)
3 2
x − 6x2 + 12 − ln 2 = 0.
4 1
В качестве двух возможных наборов кандидатур в опорные точки подходят (1, 3), (2, 1), (4, 2) или (1, 3), (2, 4),
(2, 1). Среди этих двух наборов нужно выбрать тот, для которого ширина «разделяющего коридора» больше. Для
первого набора этот коридор заключен между прямыми (они изображены на рисунке — штриховая
малиновая линия)
√
x1 − 2x2 = 0 и x1 − 2x2 = −5. Расстояние между прямыми, т. е. ширина коридора, есть 5. Для второго набора
3
точек получаем коридор, ограниченный прямыми x1 − x2 = 1, x1 − x2 = −2. Его ширина равна √ . Первый коридор
2
шире, поэтому прямая 2x1 − 4x2 = −5, проходящая через его центр, — оптимальная разделяющая, а точки (1, 3),
(2, 1), (4, 2) — опорные.
x2
bc
bc
bc
bc
bc
b
b
O
b
b
b
x1
Задача 3.
Дана обучающая выборка:
x1
x2
y
1
1
0
0 0
1 1
0 0
0 1 0
1 0 0
0 0 1
1 1
0 0
1 1
1 0
0 0
1 1
С помощью наивного байесова классификатора оценить апостериорные вероятности Pr (y | x), если (a) x1 = 1,
x2 = 0;
(b) x1 = 0, x2 = 1.
Оцениваем априорные вероятности:
Оцениваем условные вероятности:
c {X1 = 0| Y = 0} = 3 ,
Pr
5
c {Y = 0} = 1 ,
Pr
2
c {X1 = 1| Y = 0} = 2 ,
Pr
5
c {Y = 1} = 1 .
Pr
2
c {X1 = 0| Y = 1} = 2 ,
Pr
5
c {X1 = 1| Y = 1} = 3 ,
Pr
5
c {X2 = 0| Y = 0} = 1 , Pr
c {X2 = 1| Y = 0} = 4 ,
c {X2 = 0| Y = 1} = 1, Pr
c {X2 = 1| Y = 1} = 0.
Pr
Pr
5
5
Используя основное предположение наивного байесова классификатора, получаем
1
2 1 1
· ·
5 5 2
25
2
Pr {X1 = 1| Y = 0} Pr {X2 = 0| Y = 0} Pr {Y = 0}
=
=
Pr {Y = 0| X1 = 1, X2 = 0} =
≈
,
Pr {X1 = 1, X2 = 0}
17
3
1
17
+
25 10
50
3
1
3
·1·
5
2
10
15
Pr {X1 = 1| Y = 1} Pr {X2 = 0| Y = 1} Pr {Y = 1}
≈
=
=
Pr {Y = 1| X1 = 1, X2 = 0} =
Pr {X1 = 1, X2 = 0}
17
1
17
3
+
25 10
50
(знаменатели в двух формулах выше равны сумме всех числителей и, следовательно окончательные оценки апостериорных вероятностей получаются после вычисления всех числителей).
3 4 1
6
· ·
5 5 2
25
Pr {X1 = 0| Y = 0} Pr {X2 = 1| Y = 0} Pr {Y = 0}
Pr {Y = 0| X1 = 0, X2 = 1} =
≈
= 1,
=
Pr {X1 = 0, X2 = 1}
6
6
+0
25
25
2
1
·0·
5
2
0
Pr {X1 = 0| Y = 1} Pr {X2 = 1| Y = 1} Pr {Y = 1}
≈
= 0.
=
Pr {Y = 1| X1 = 0, X2 = 1} =
Pr {X1 = 0, X2 = 1}
6
6
+0
25
25